Describing probability distributions and probability distributions with muultiple variables - Week 2

Lesson 1 - Describing Distributions

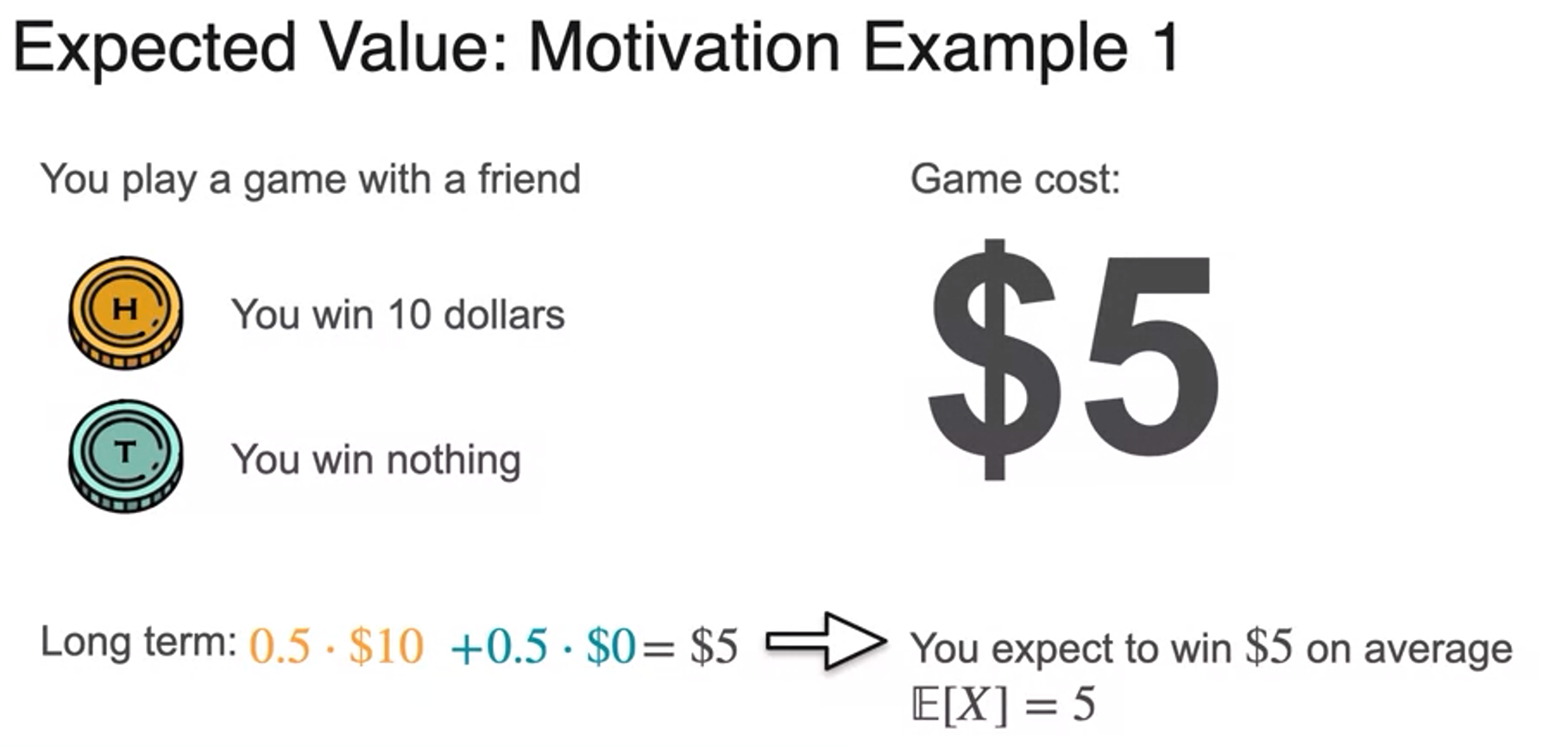
Expected Value

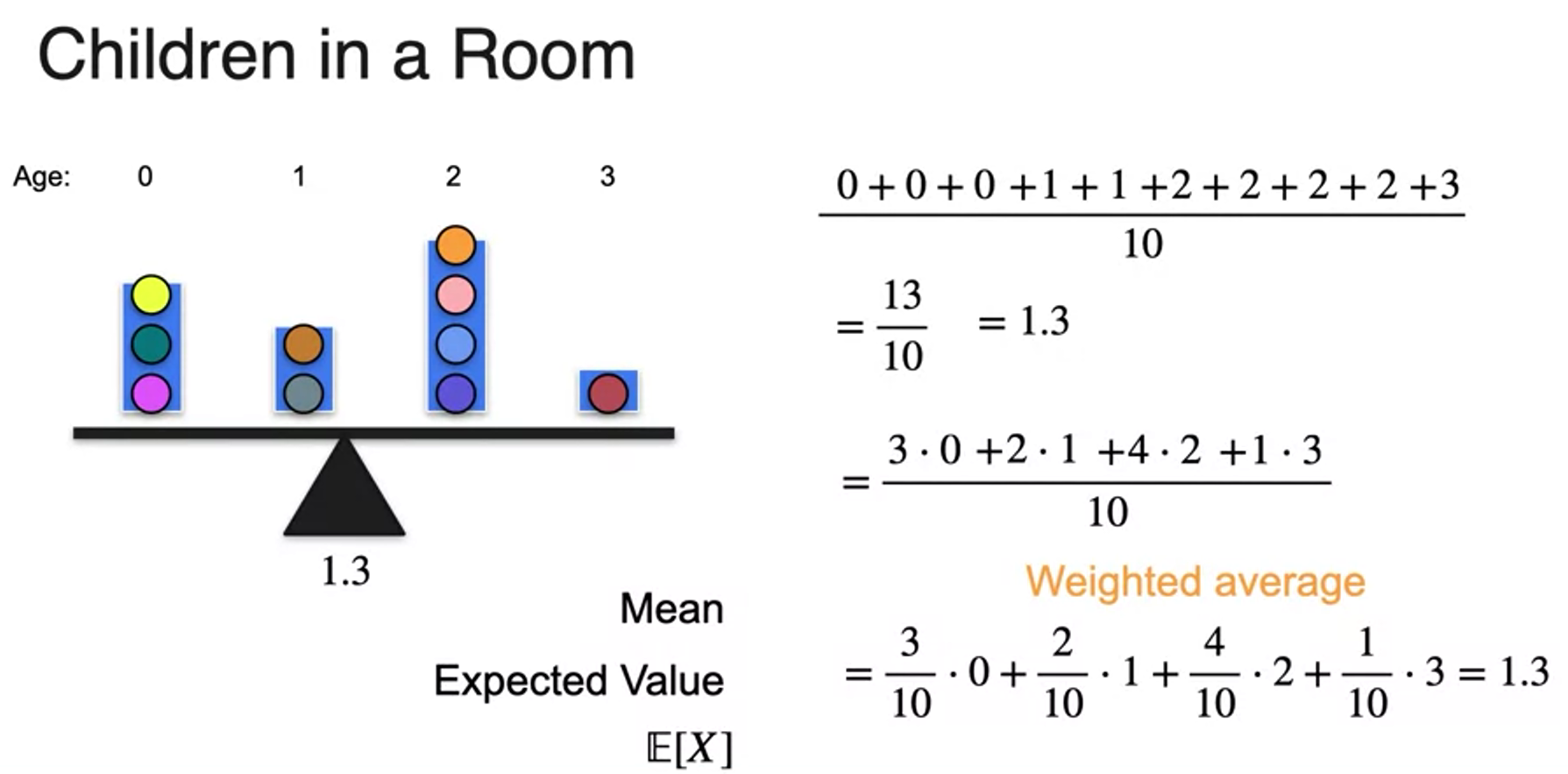
• expected value is E of x ; $\mathbb{E}[X]$

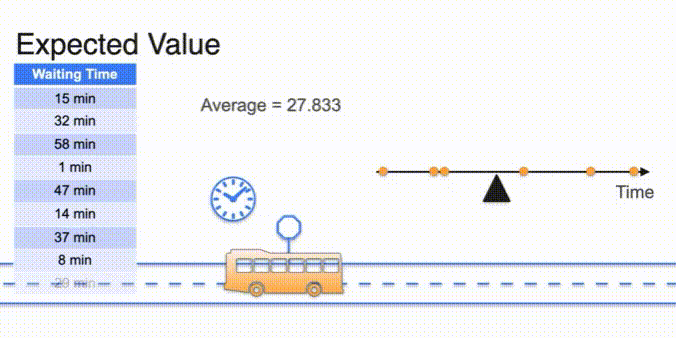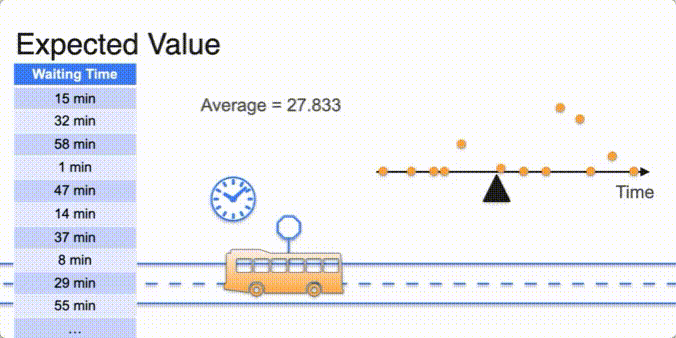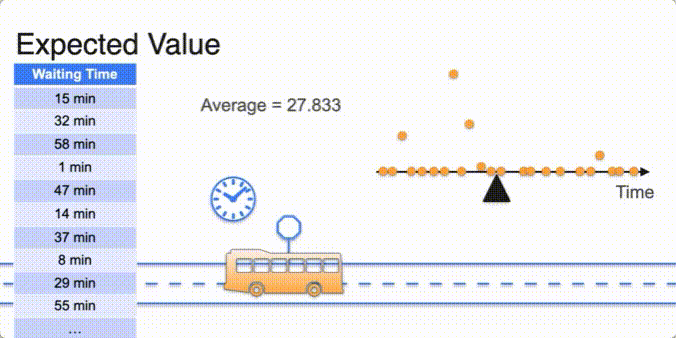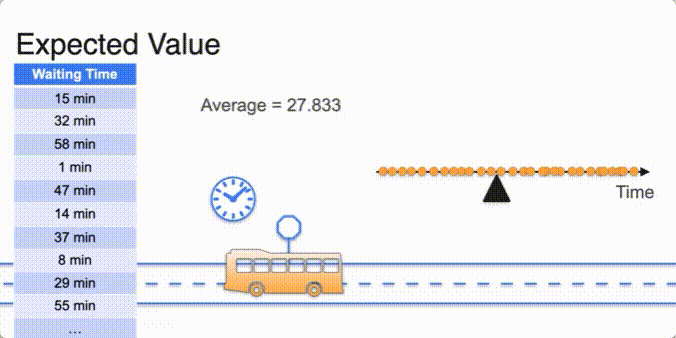
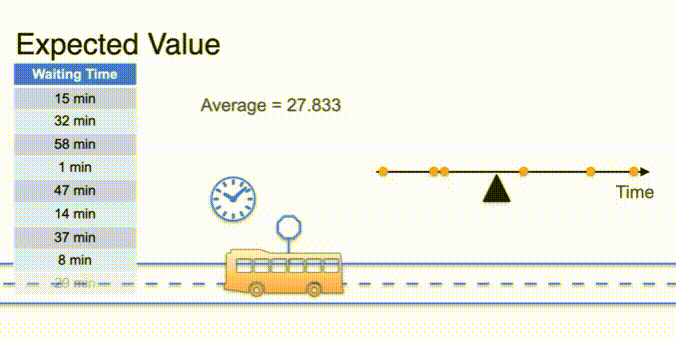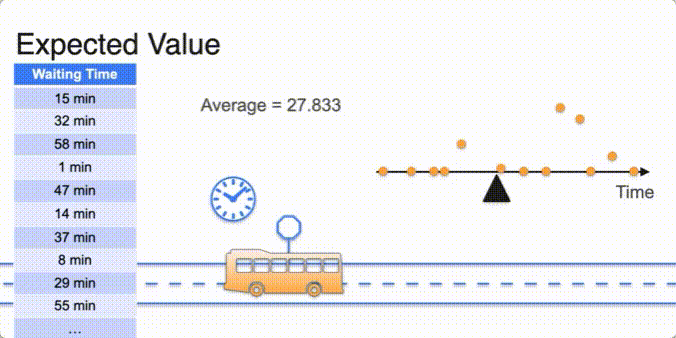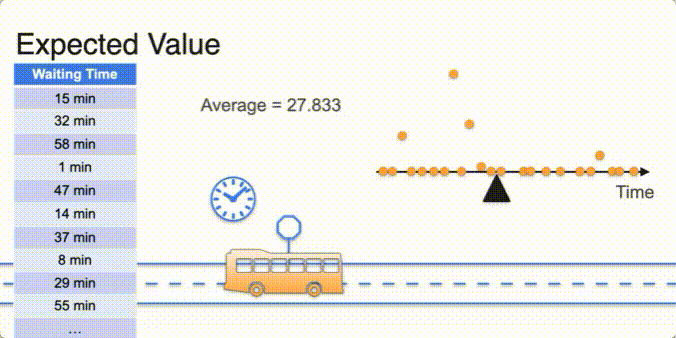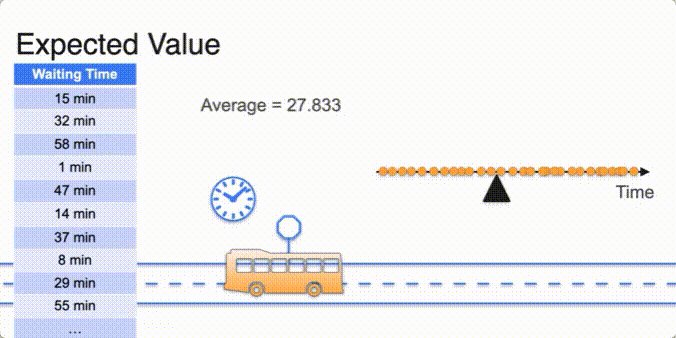
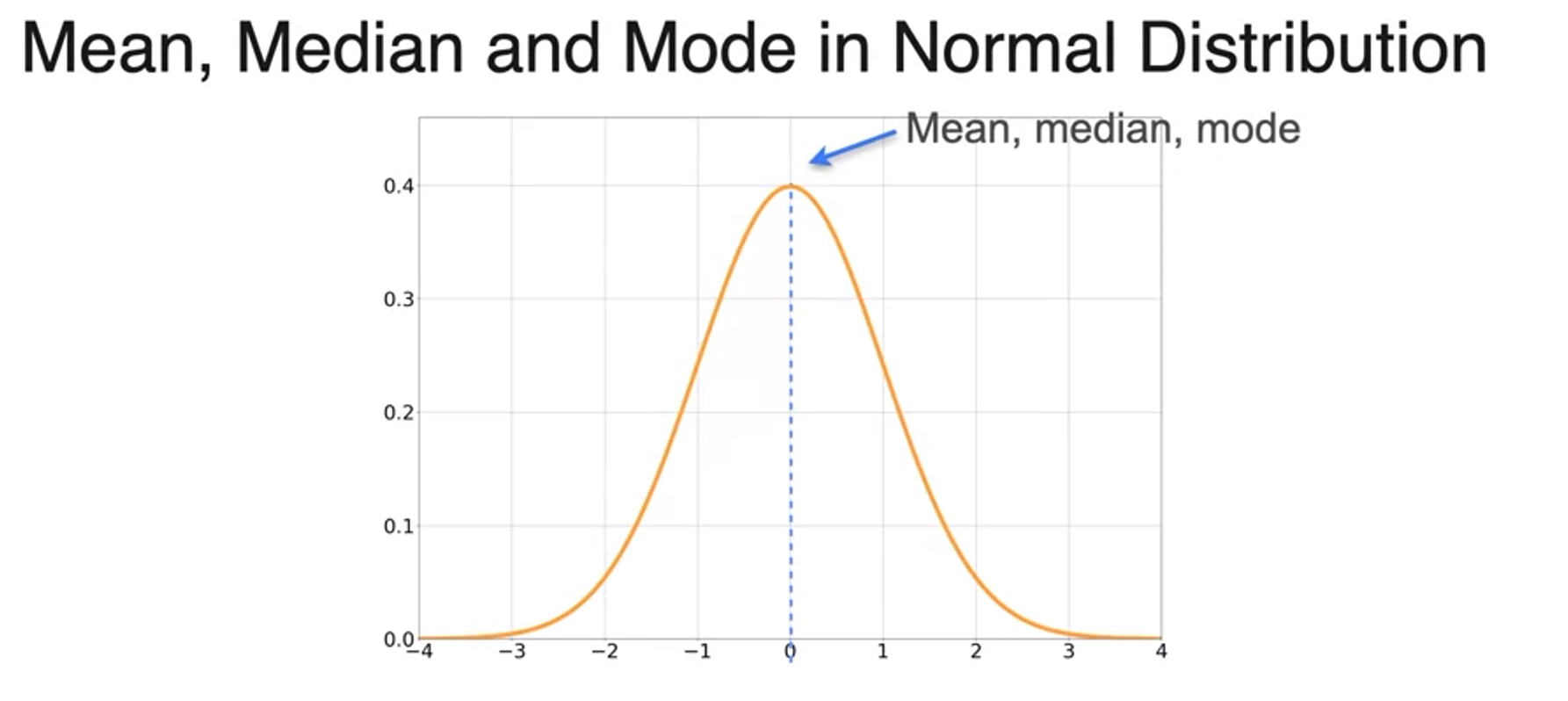
• Uniform distribution avg in the middle

• its median

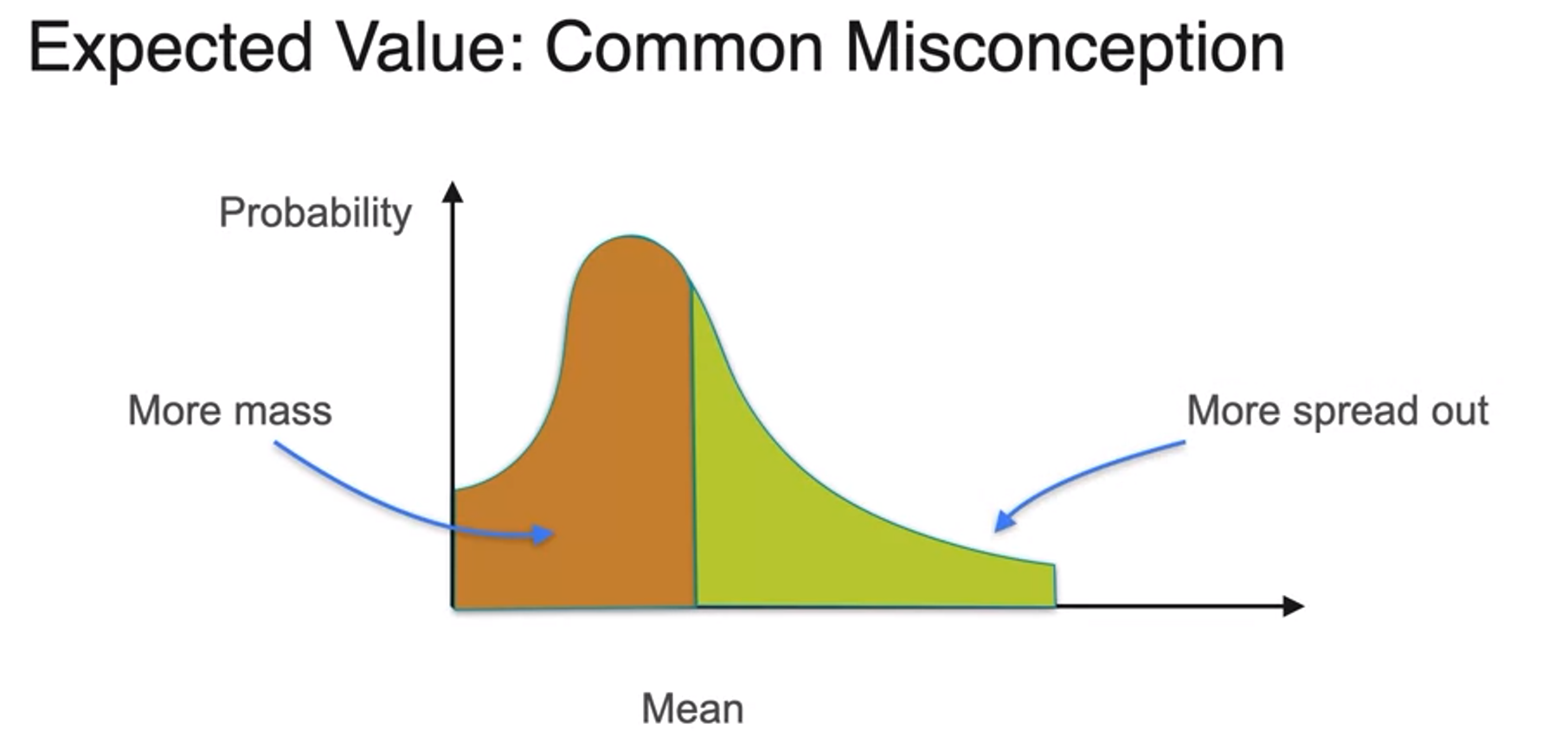
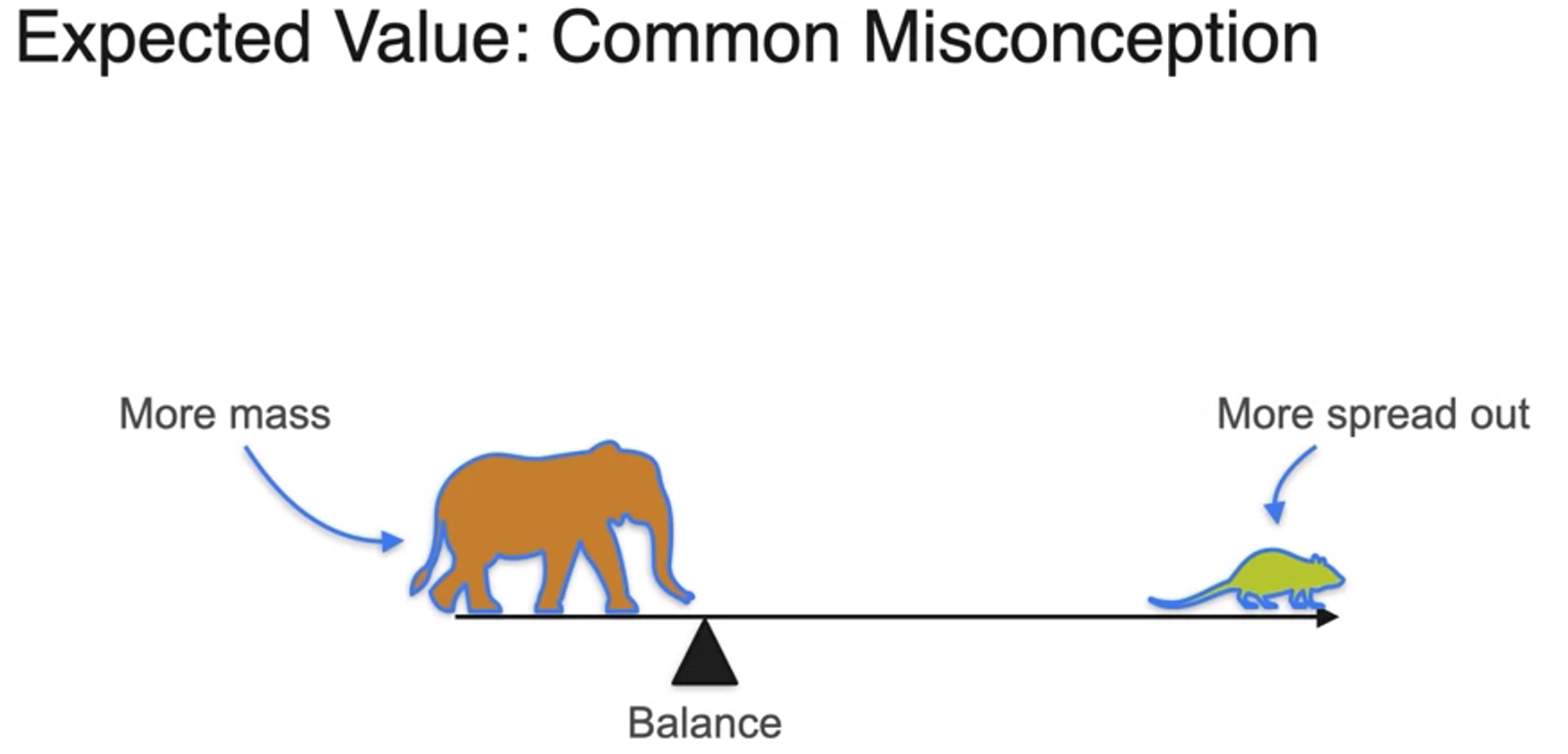
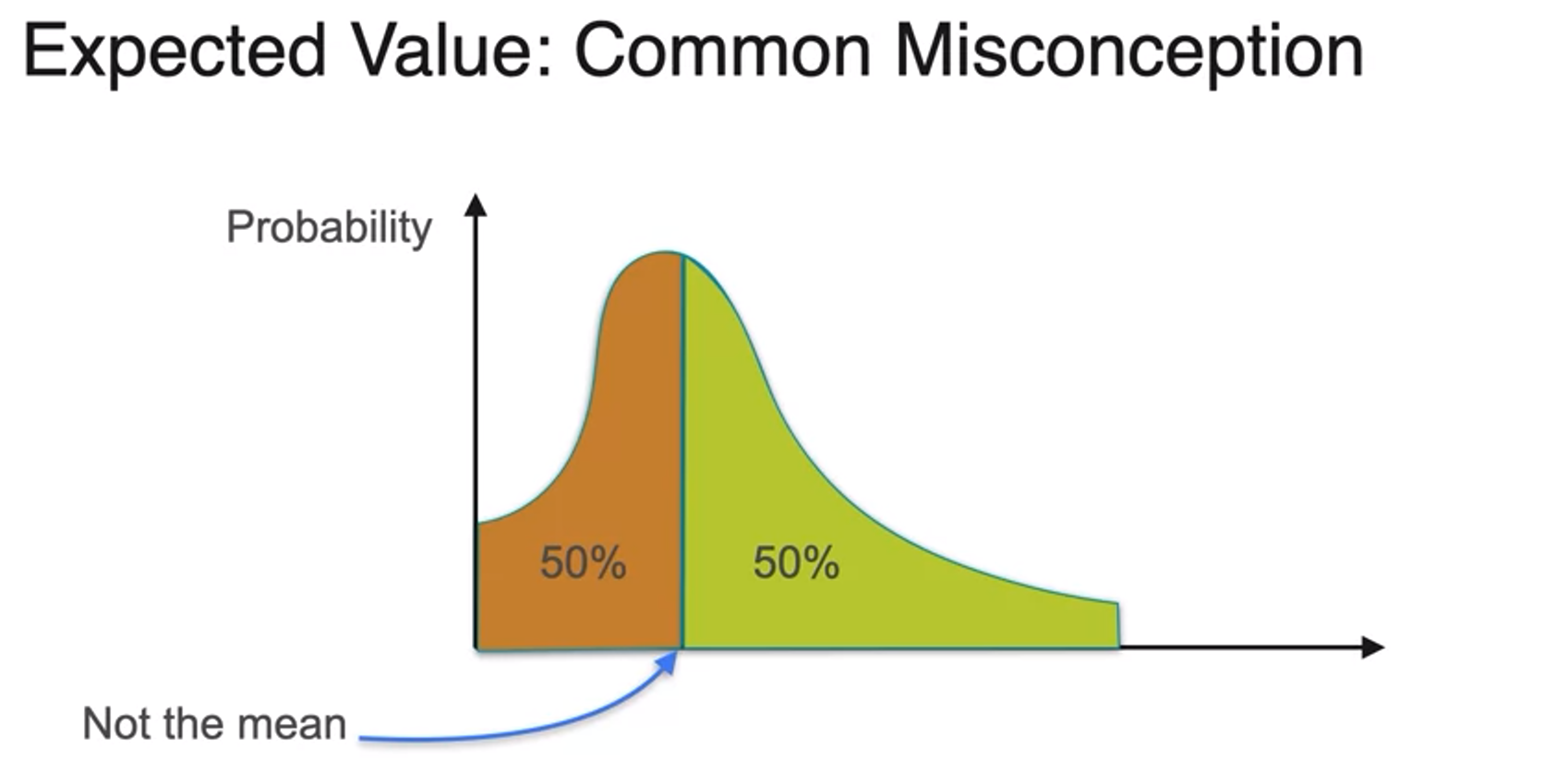
• concept of torque : force times length

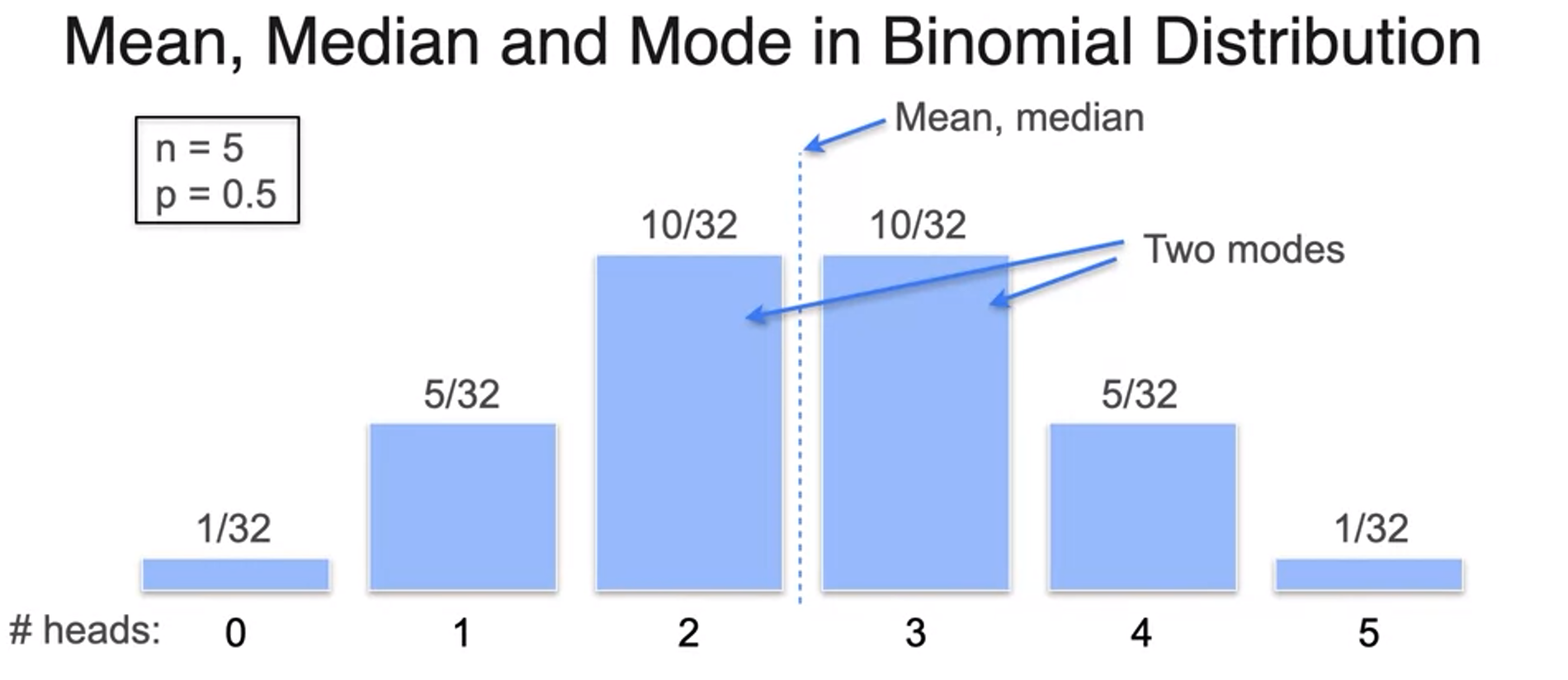
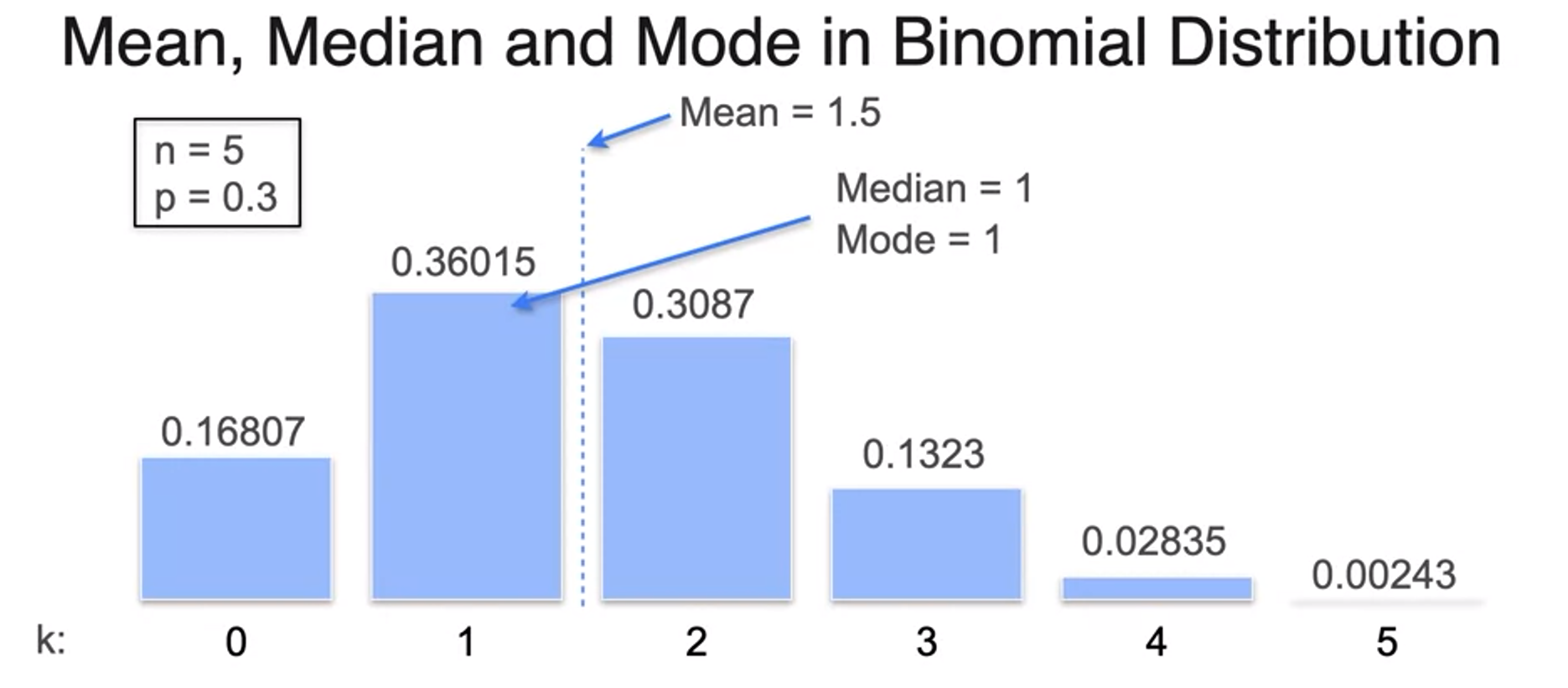
Other measures of central tendency: median and mode

• 마이클 조던이 캐리한 지리학과 졸업자 초봉

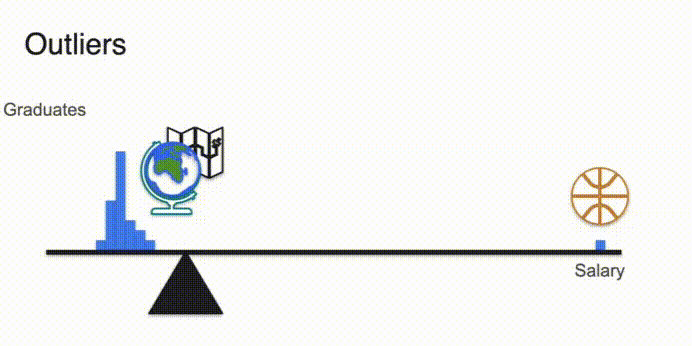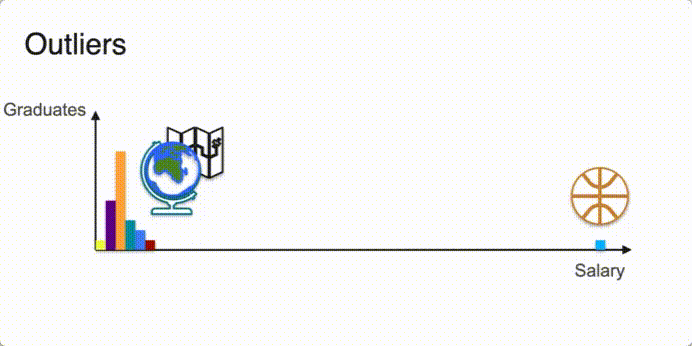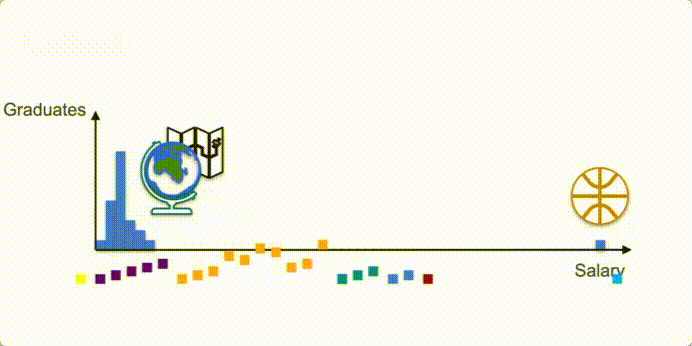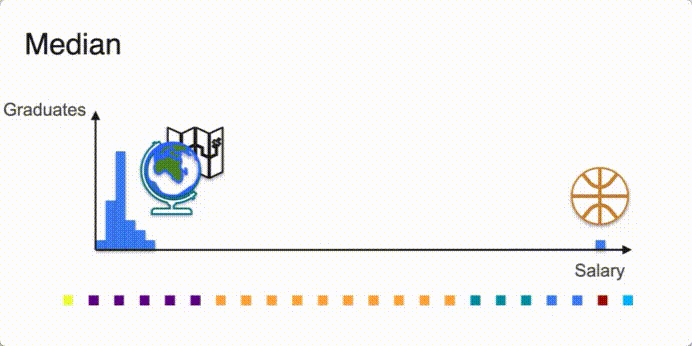
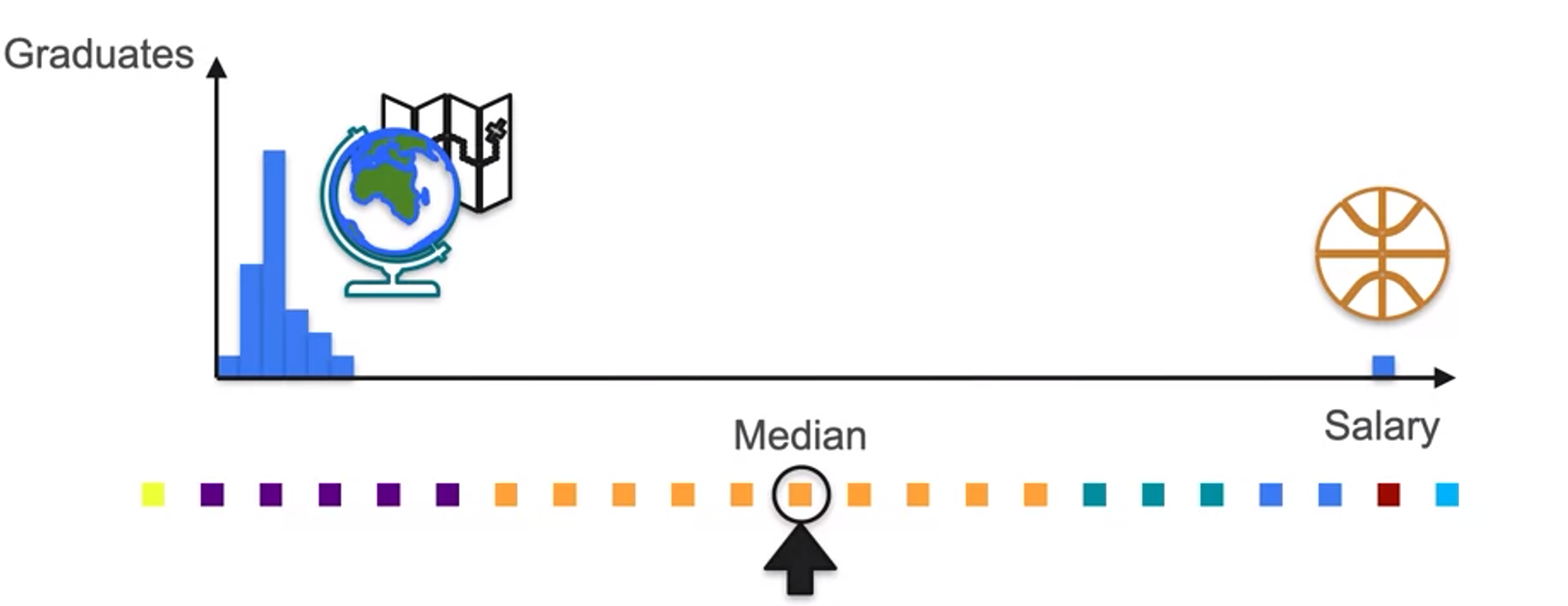
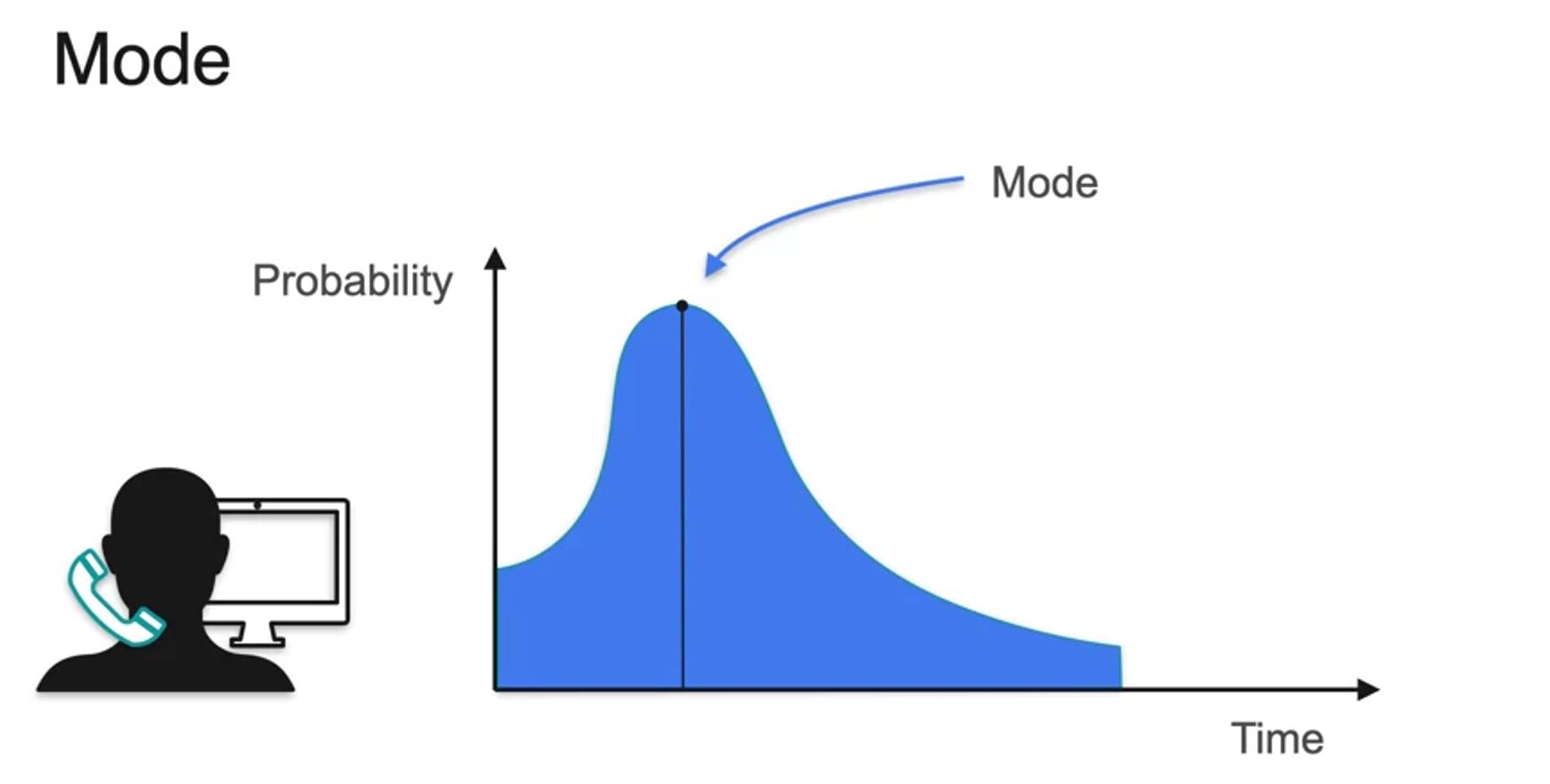
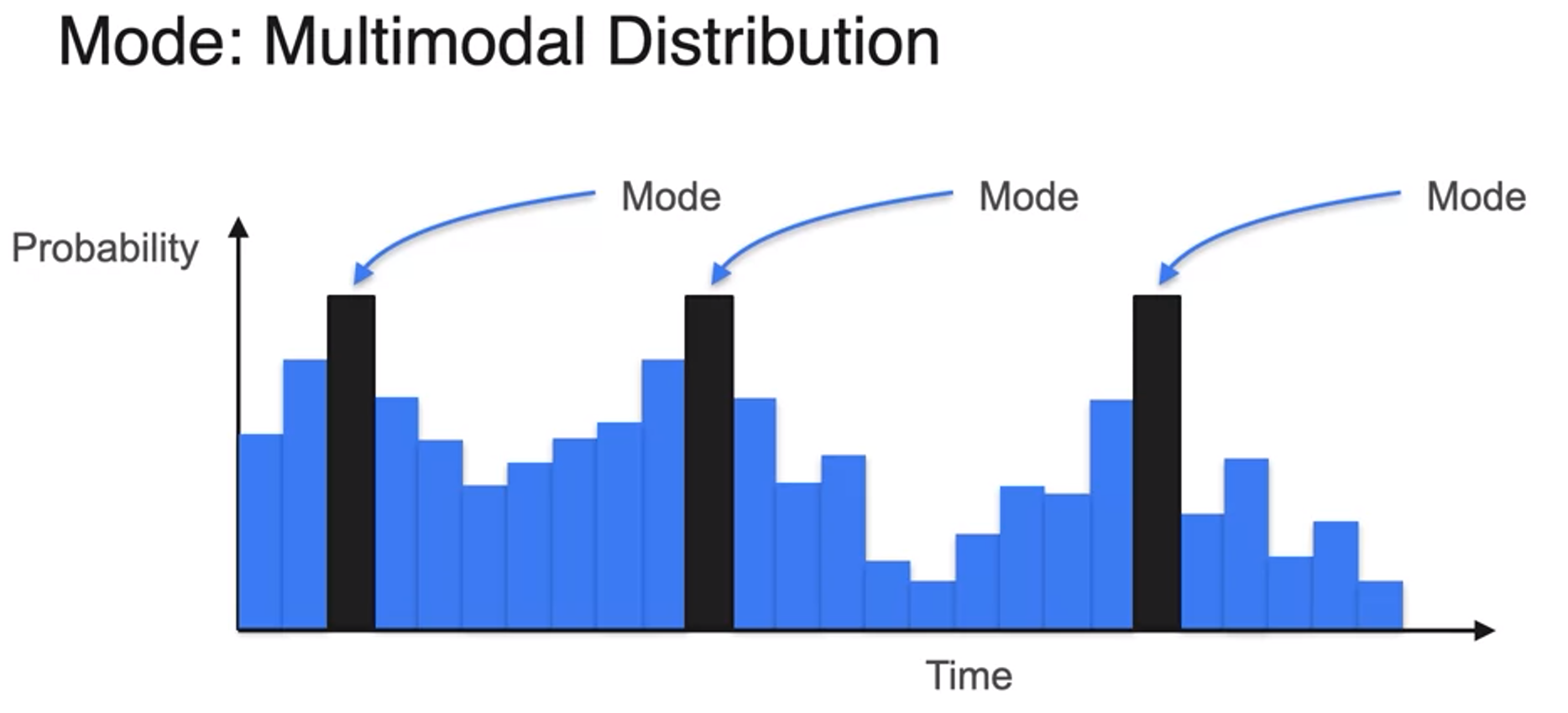
• Not unique mode? -> Multimodal Distribution다봉분포

Expected value of a Function

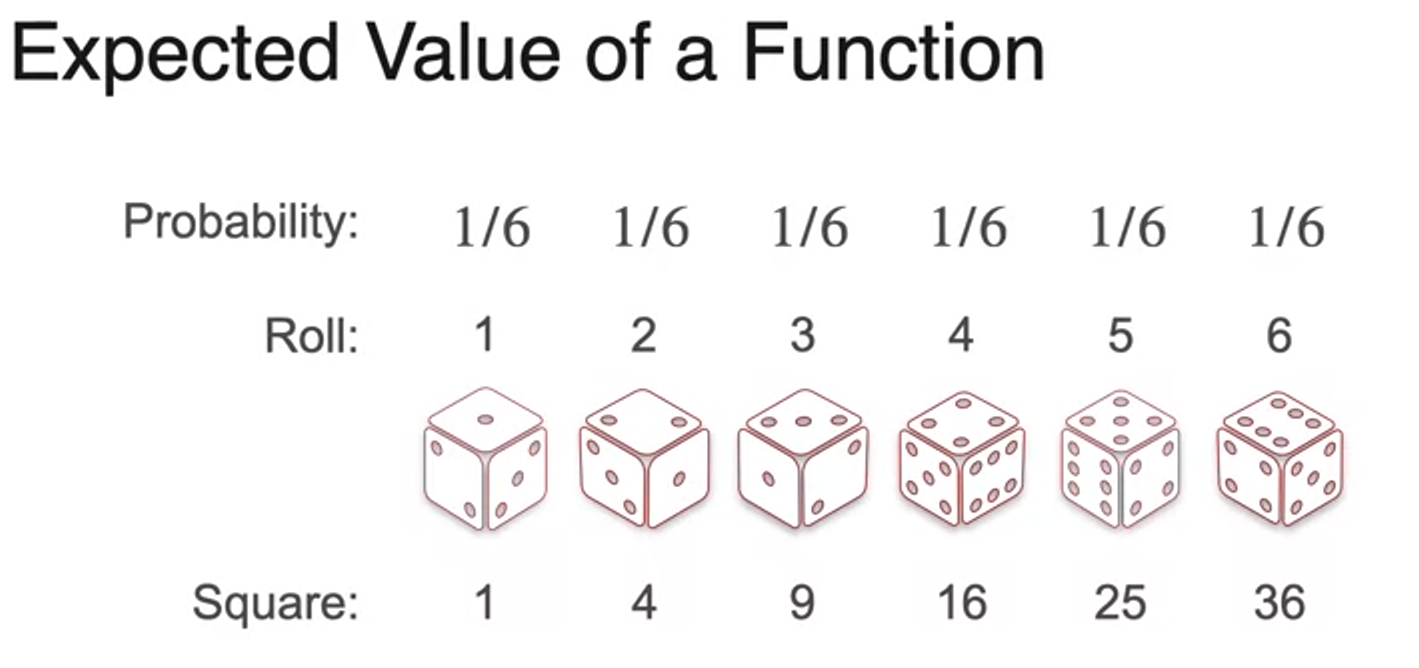
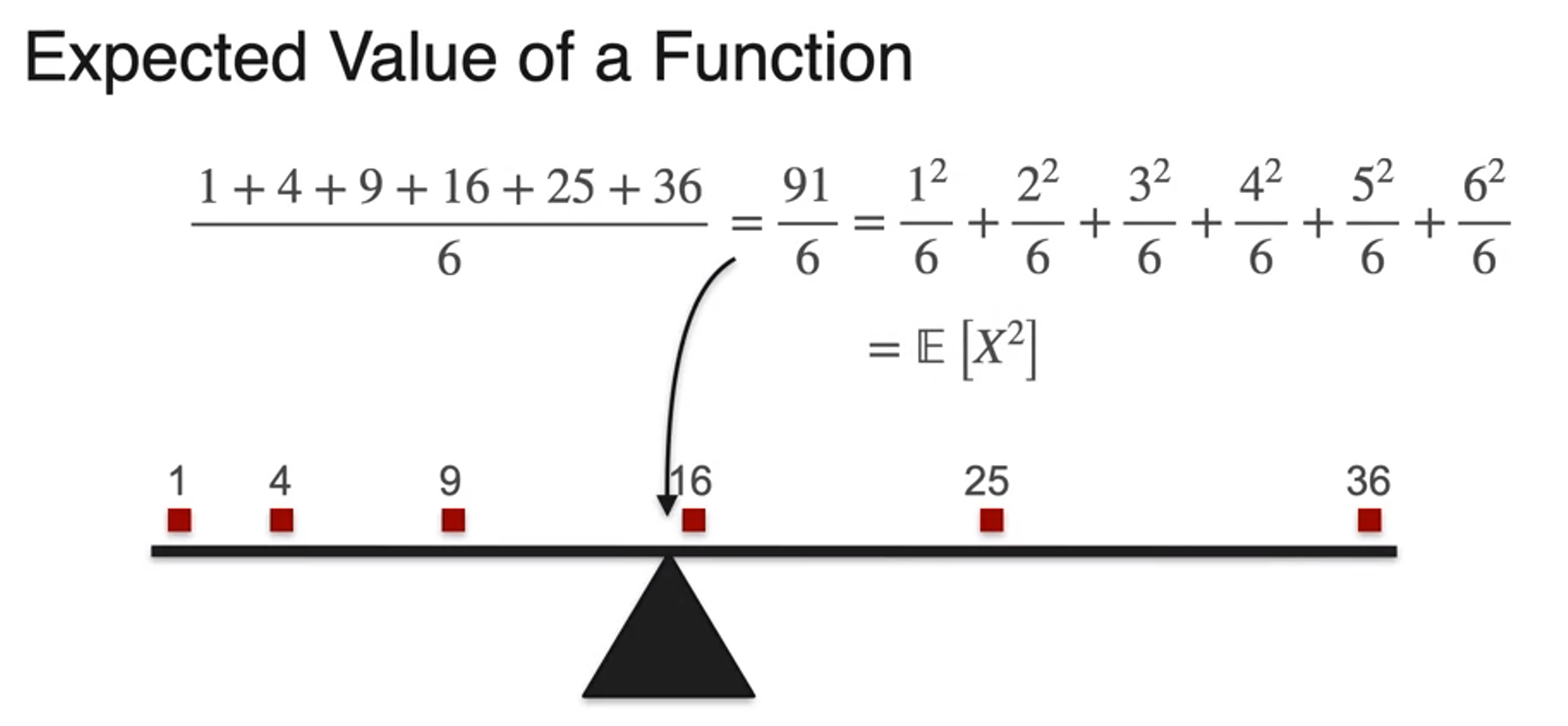
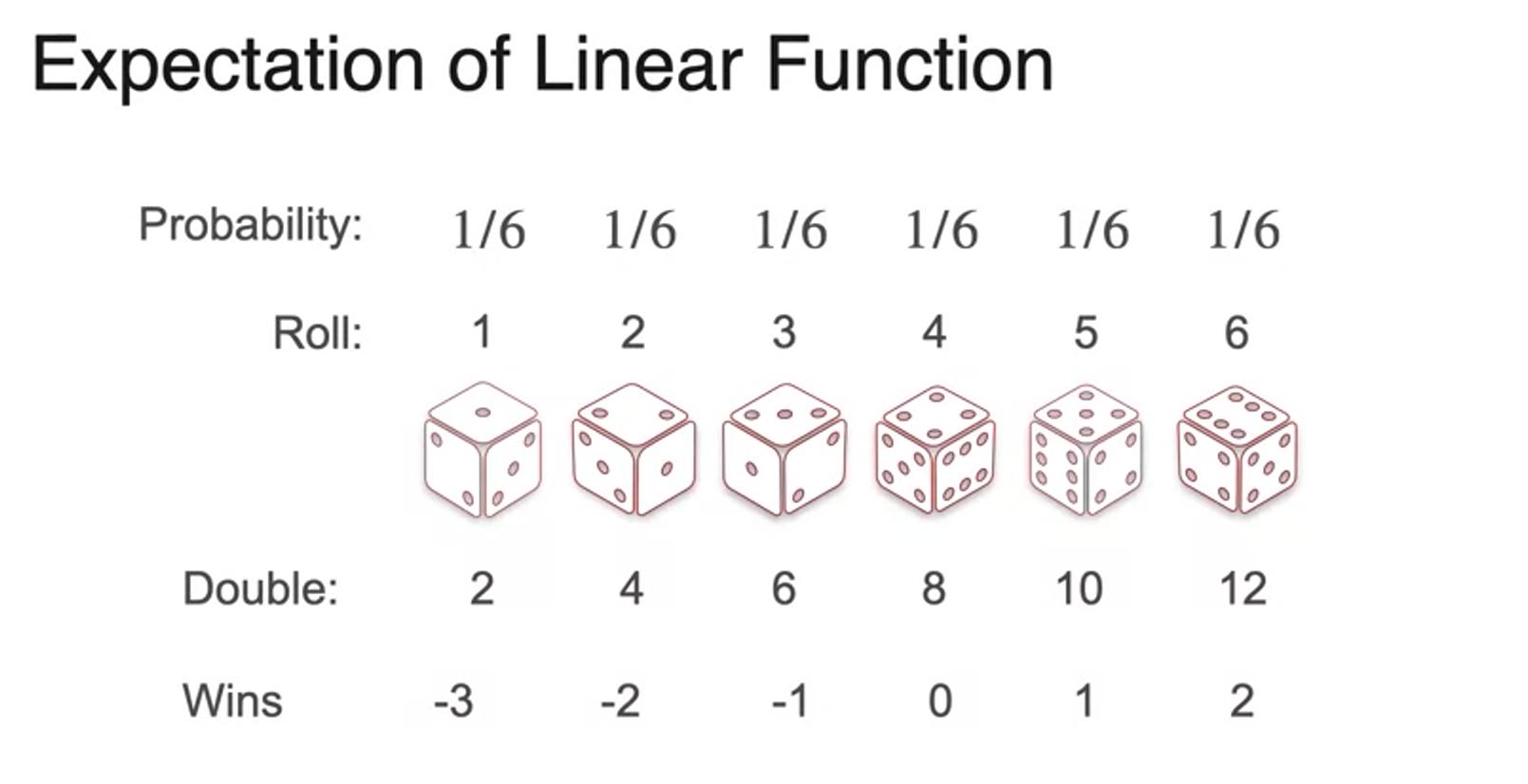
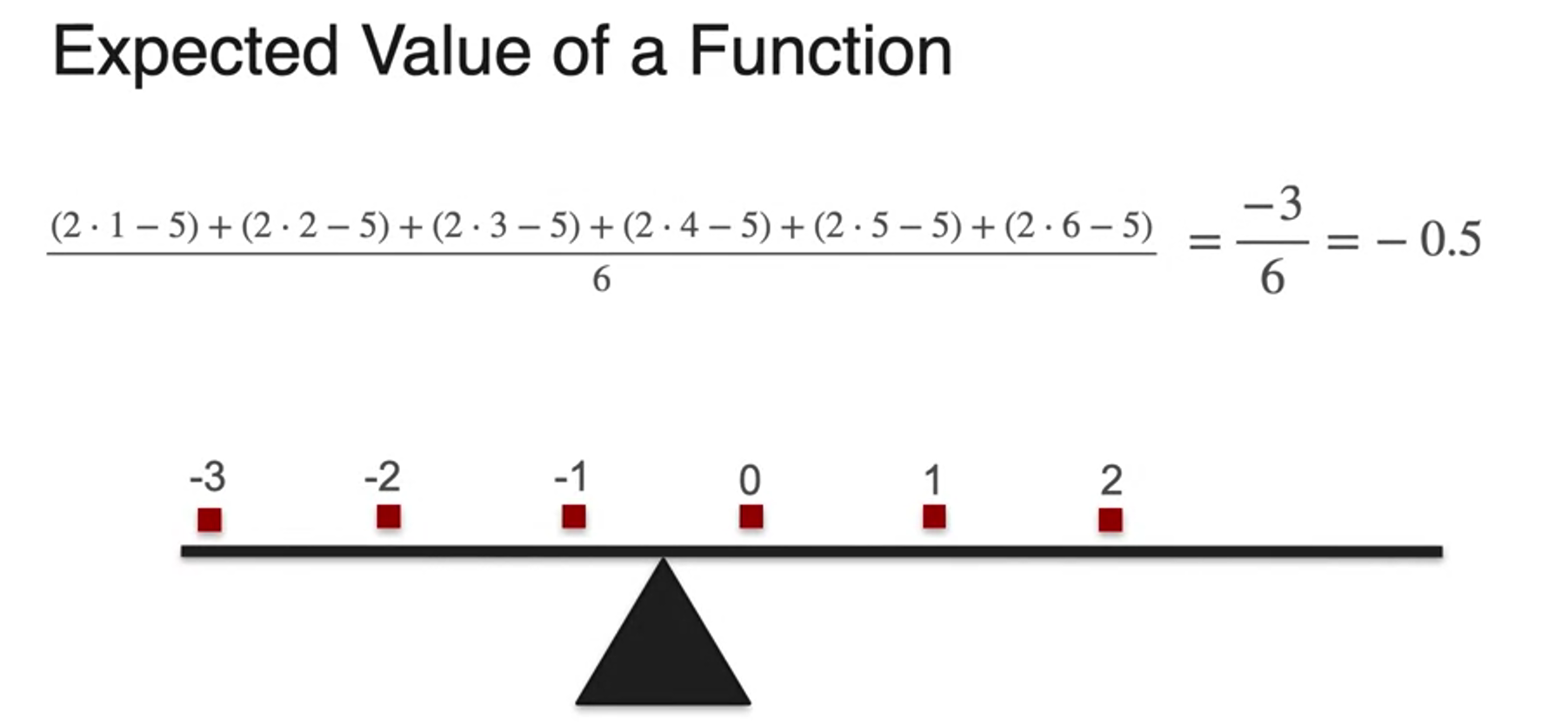
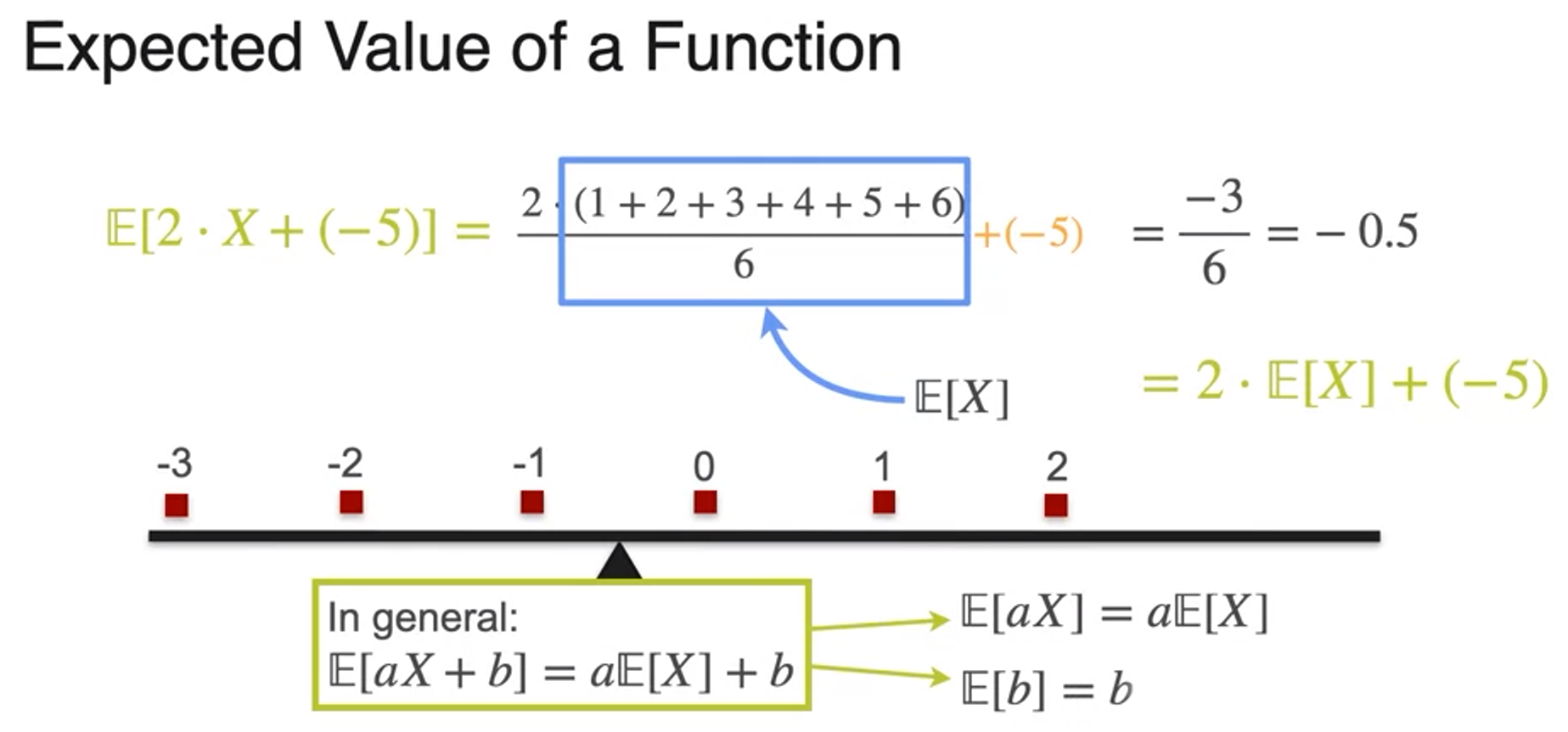
• expectation is a linear operator
  • $\mathbb{E}[aX]$ = $a\mathbb{E}[X]$
  • $\mathbb{E}[b]$ = $b$
    expected value of constant is constant

Sum of expectations

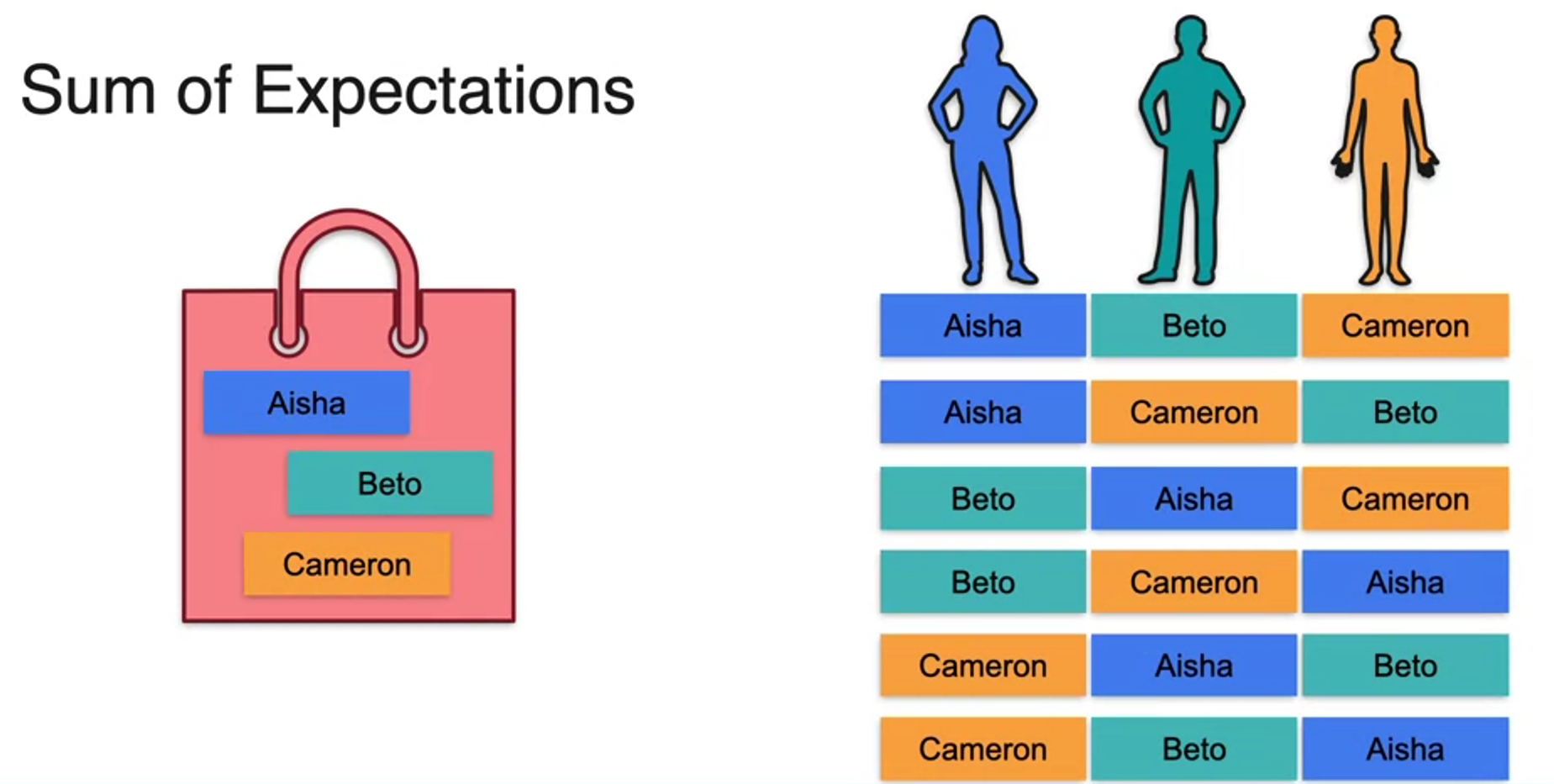
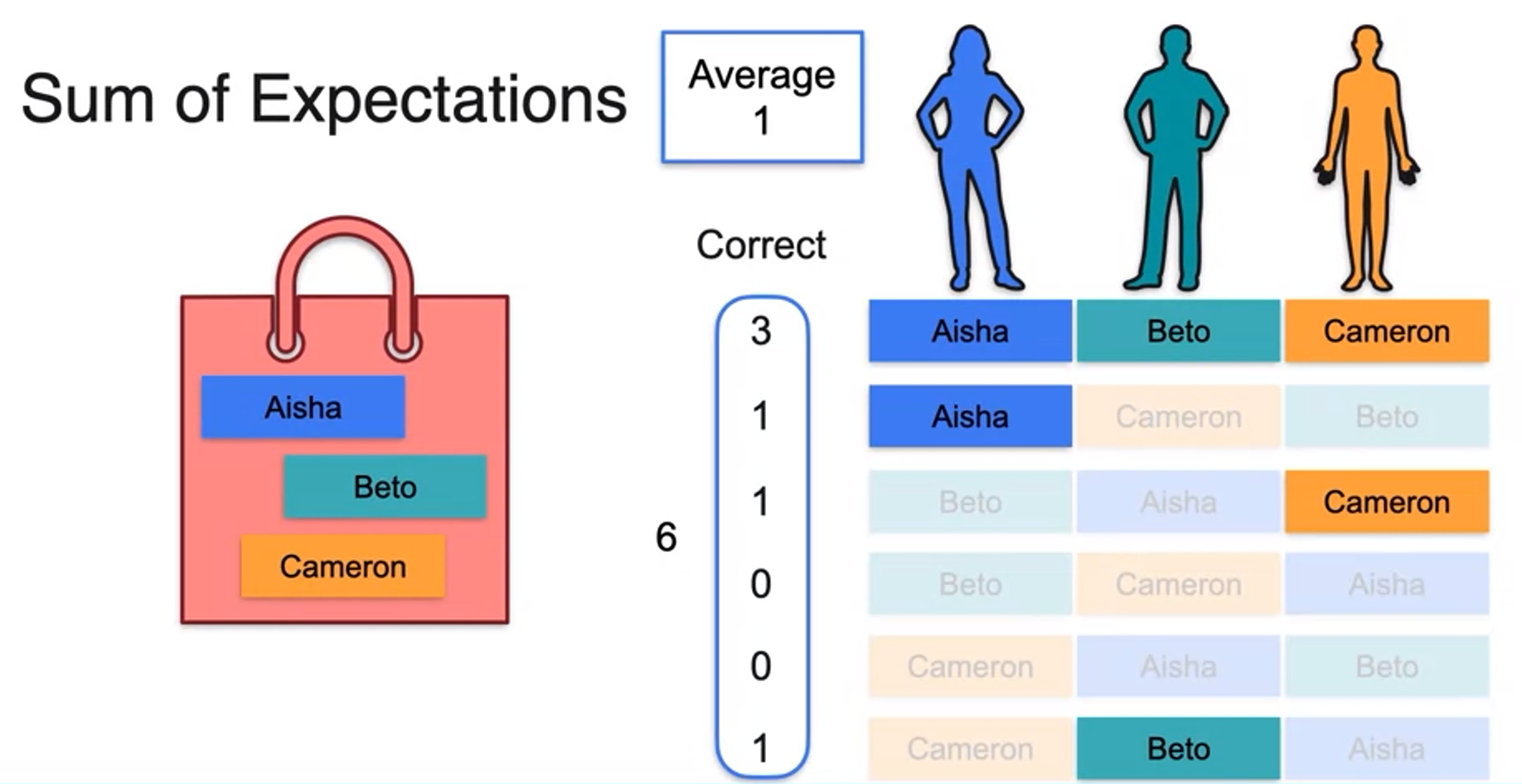
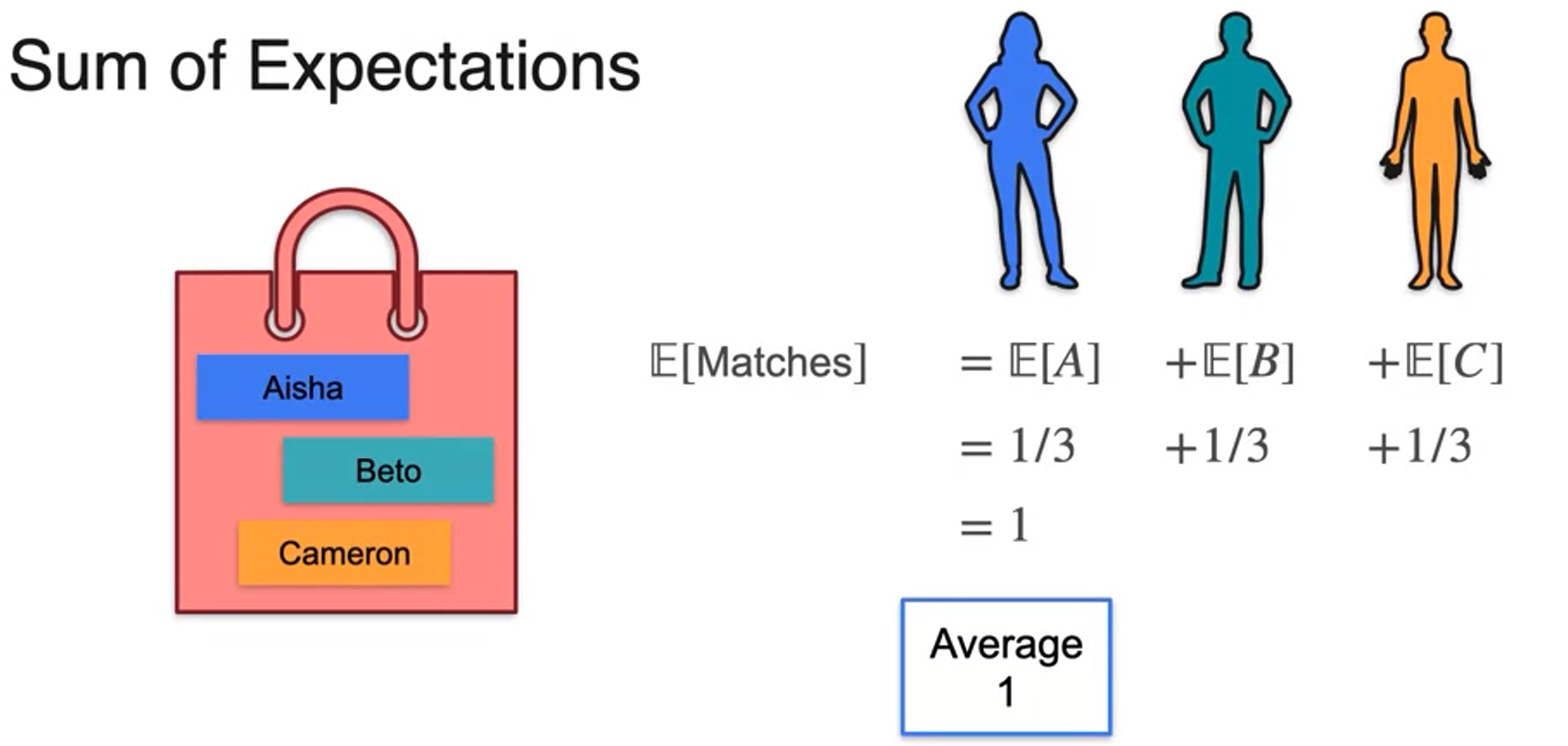
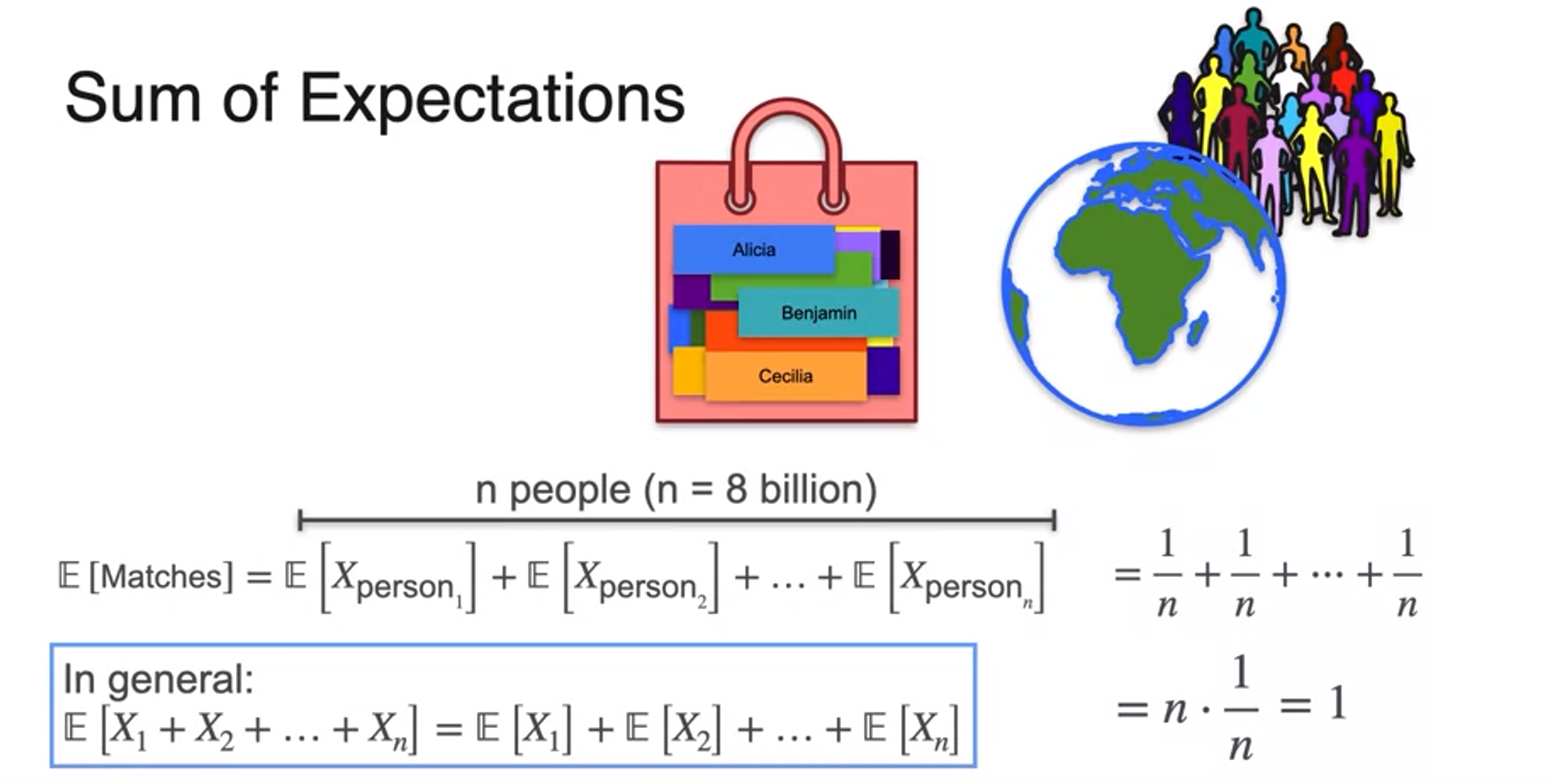
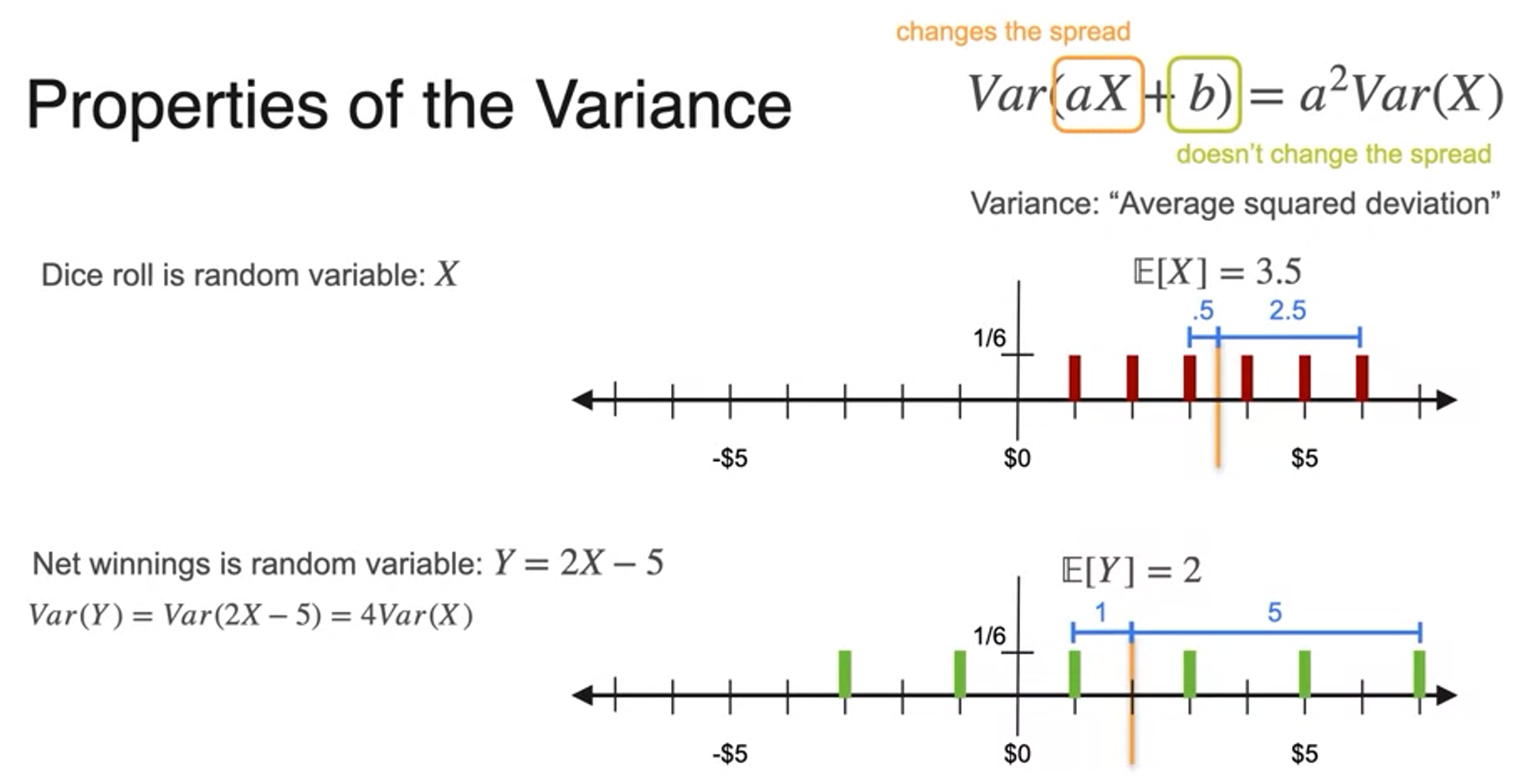
Variance

• variance

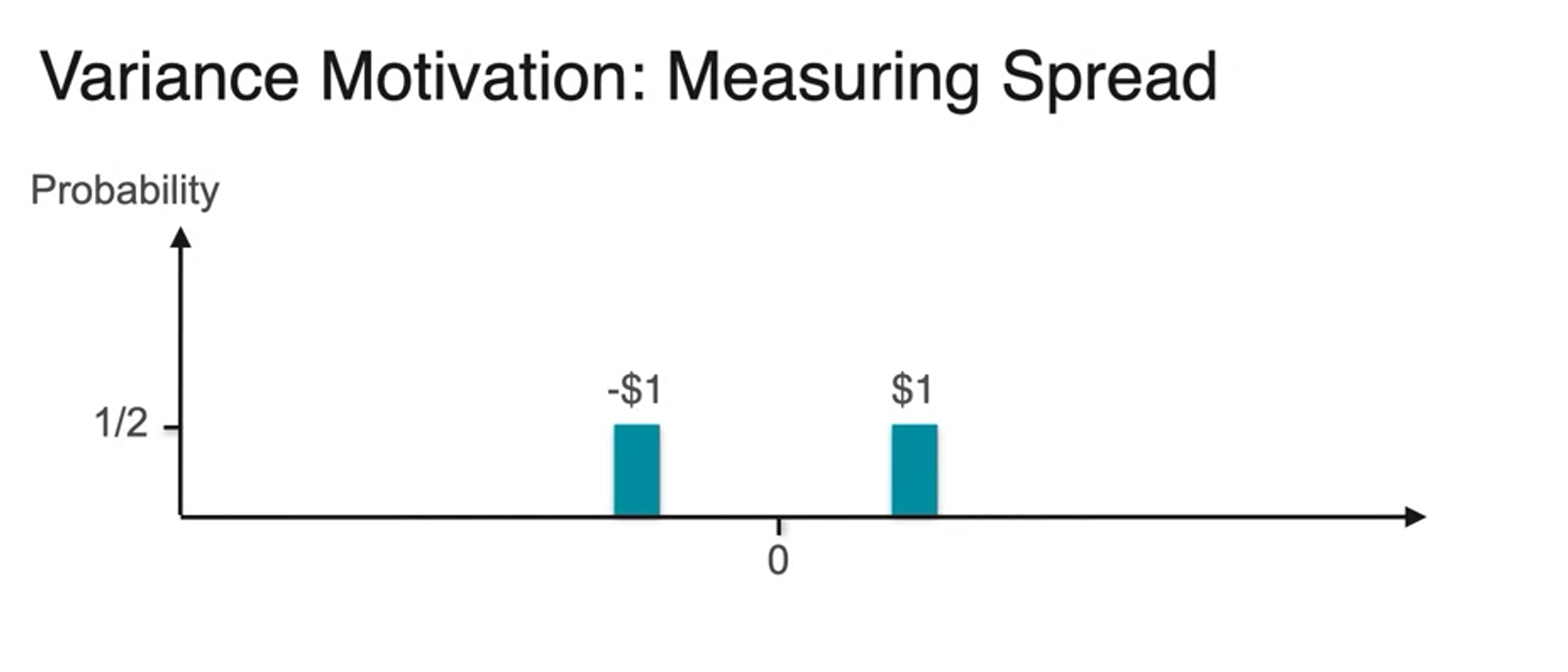
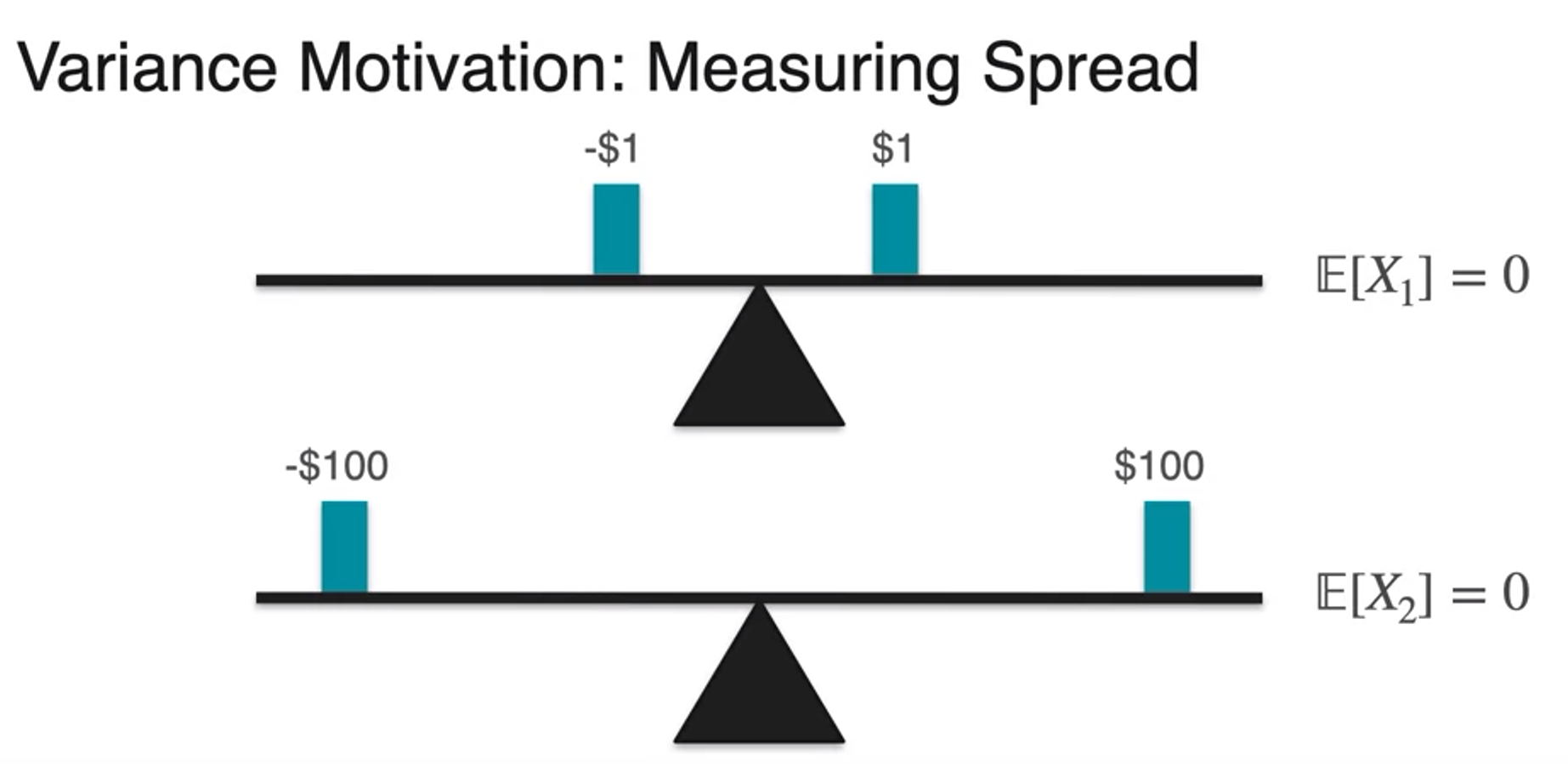
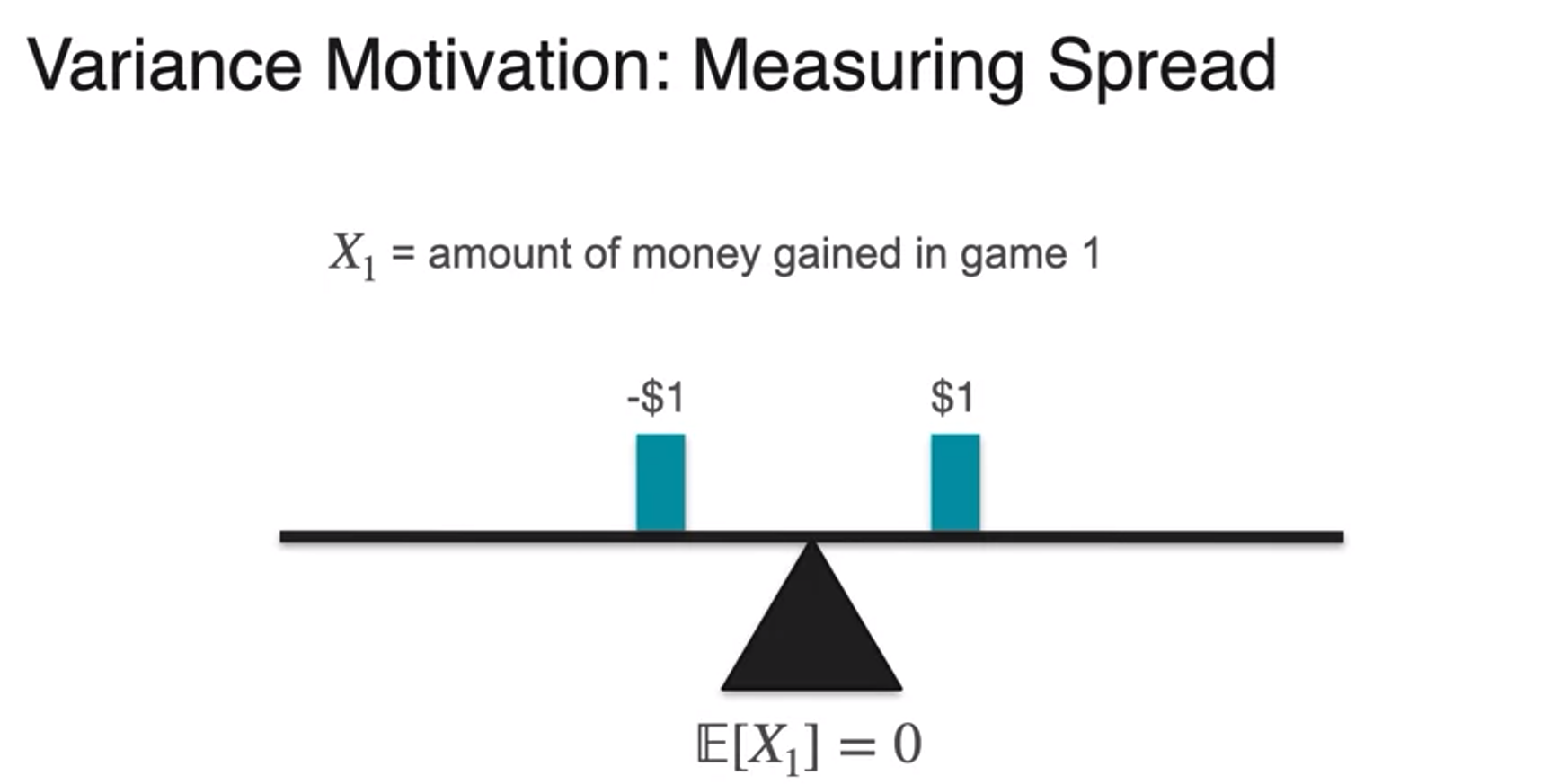
• plotting first board game

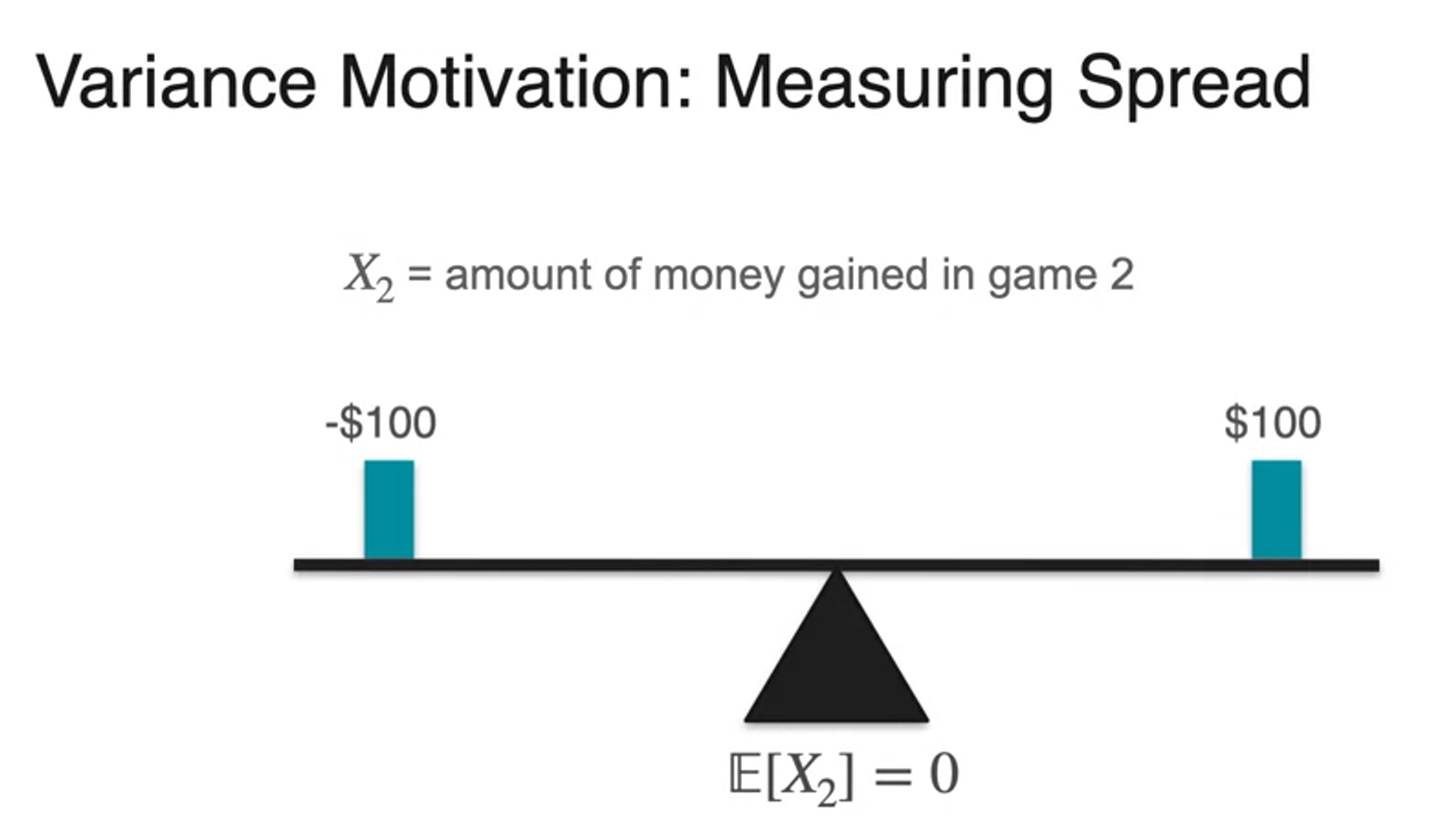
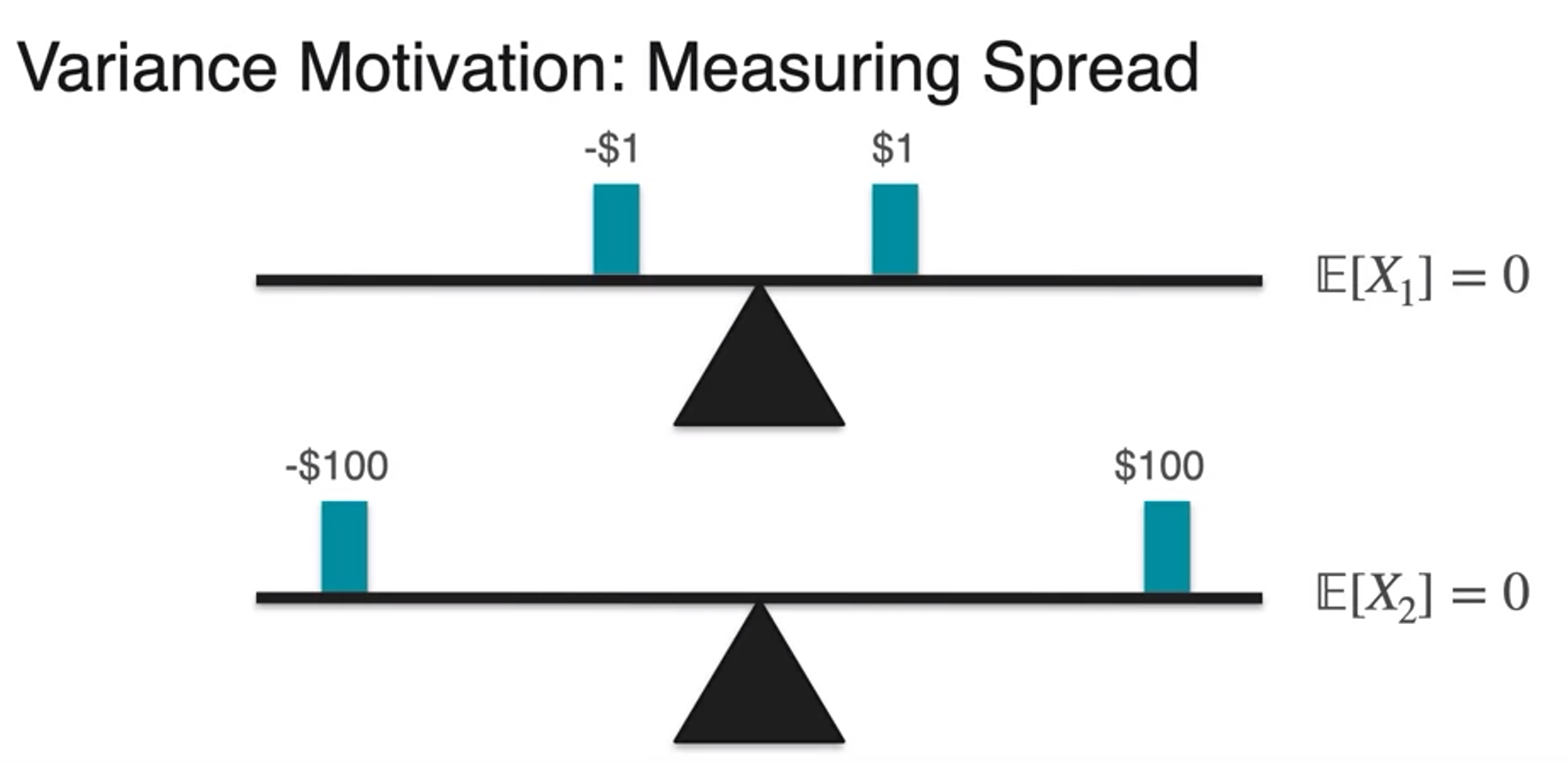
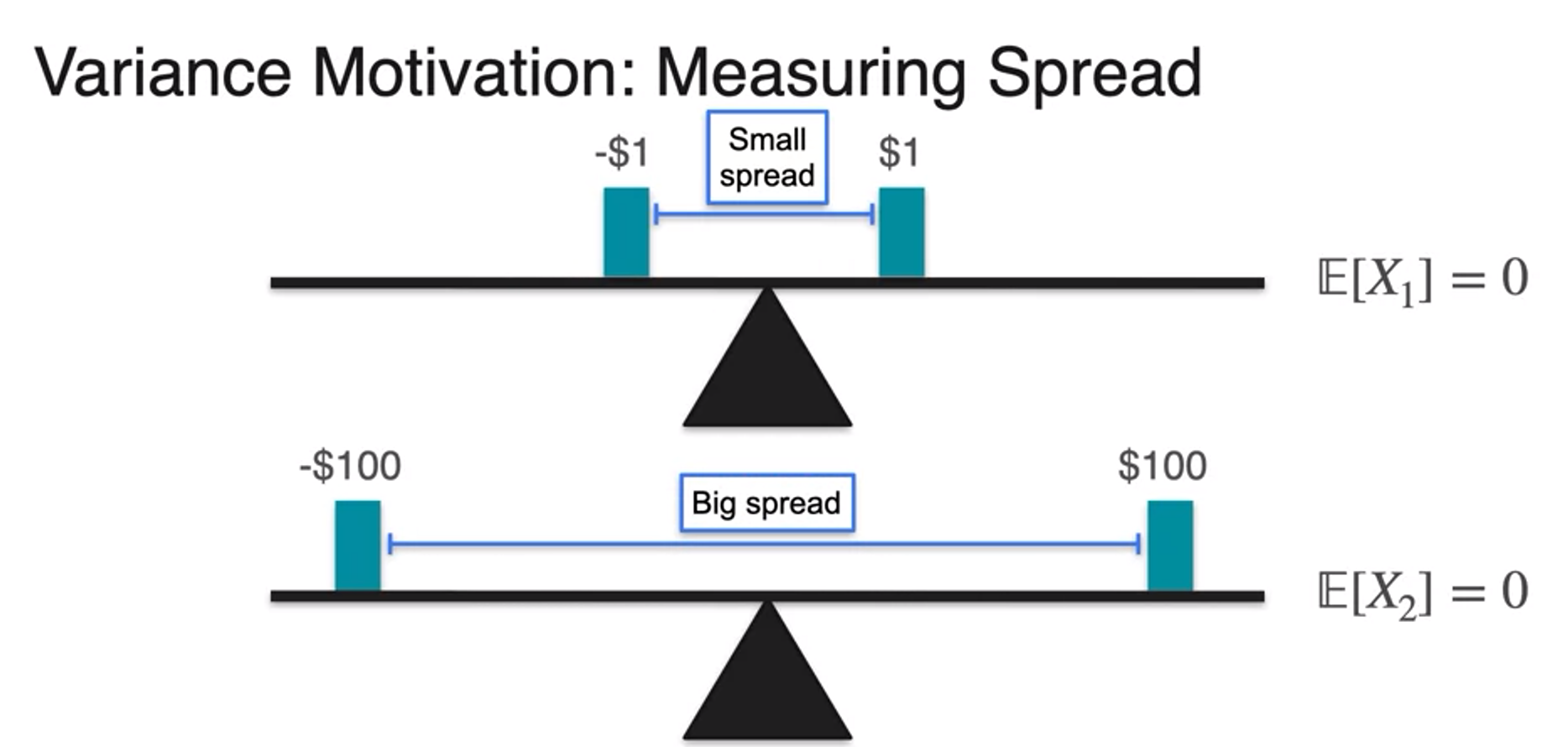
• quantify this difference in spread

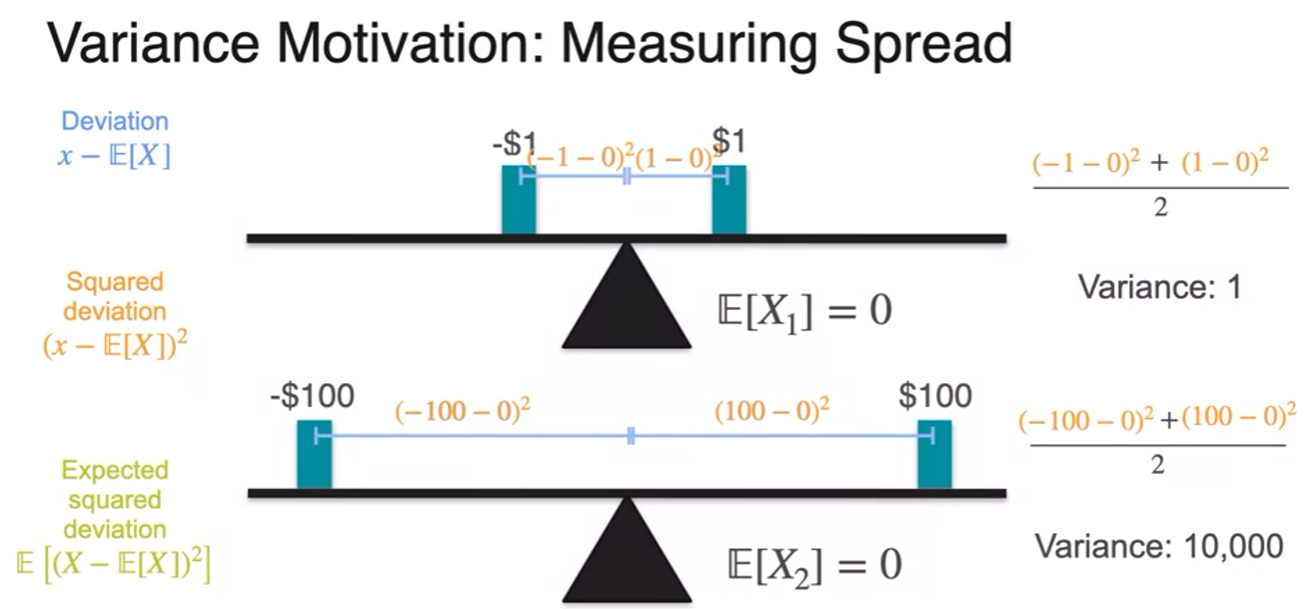
w

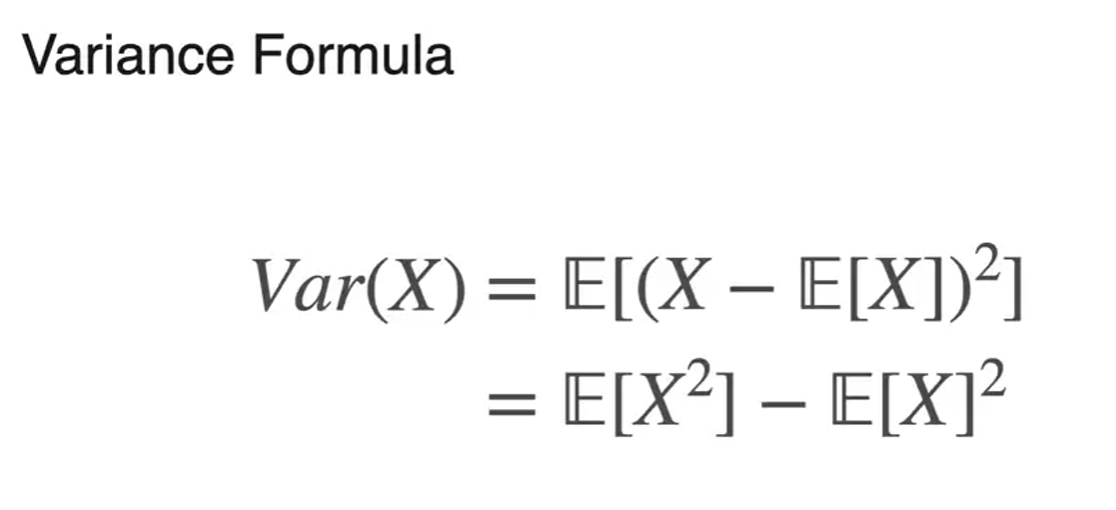
Standard Deviation

• 표준 편차Standard Deviation

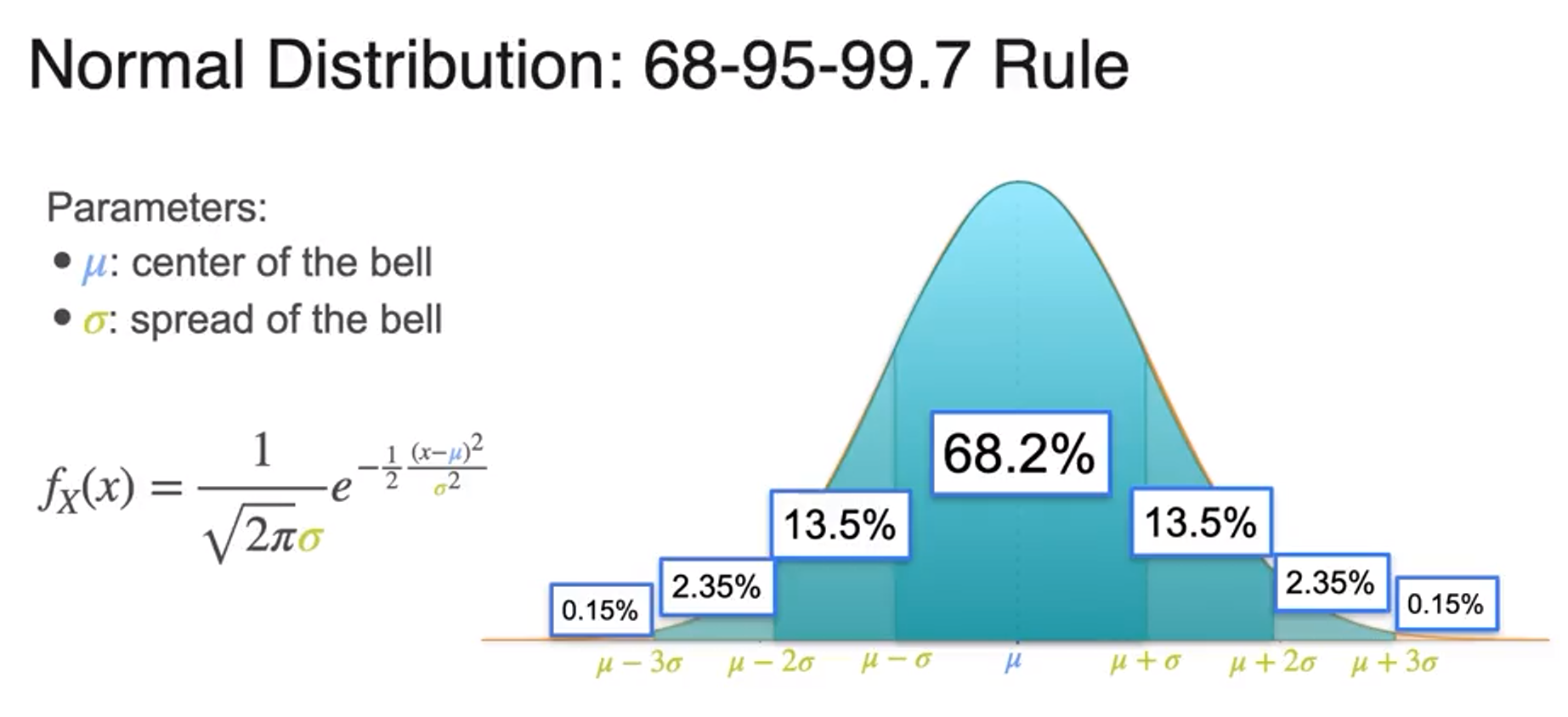
• 정규 분포Normal distribution

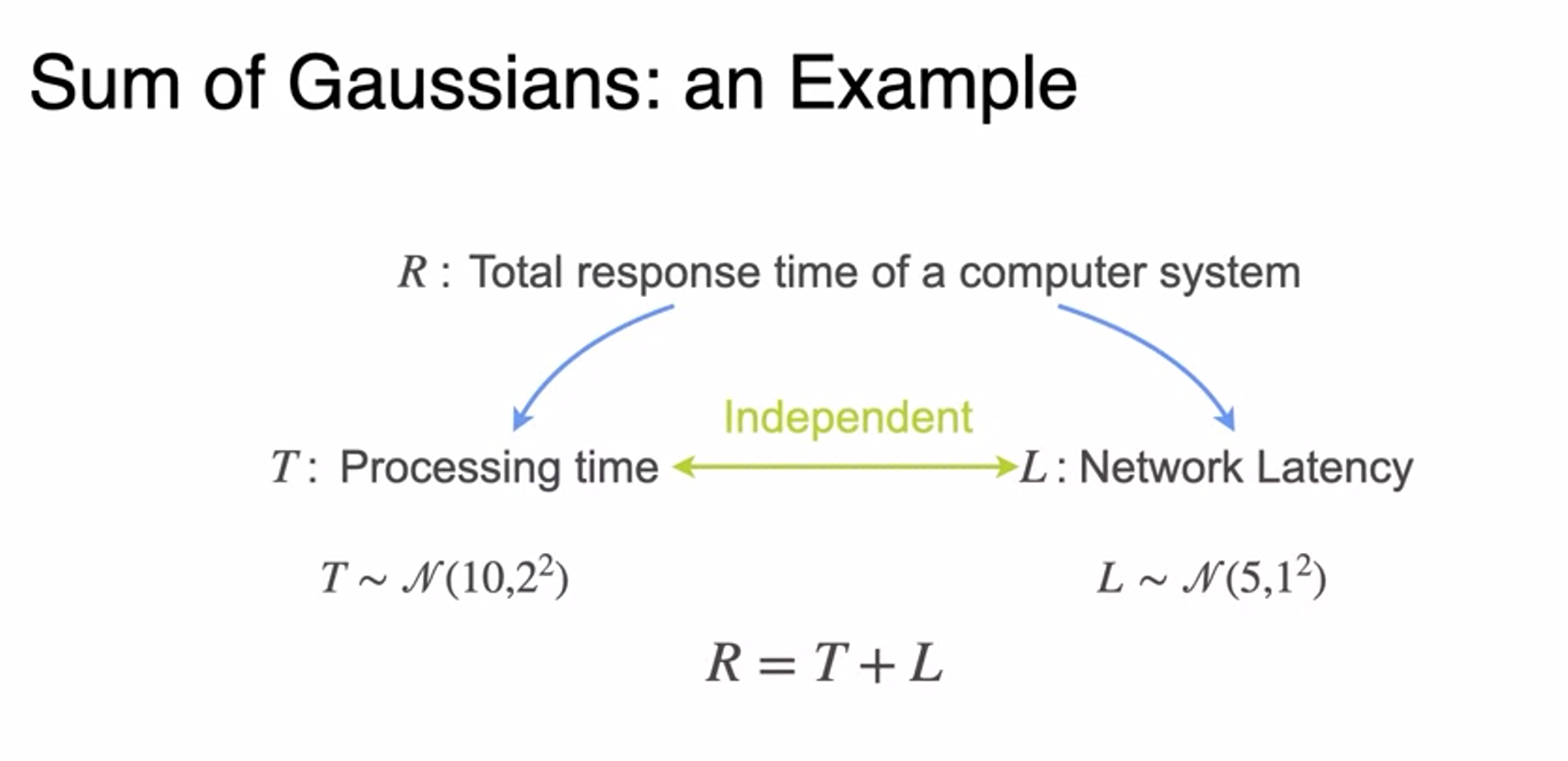
Sum of Gaussians

Standardizing a Distribution

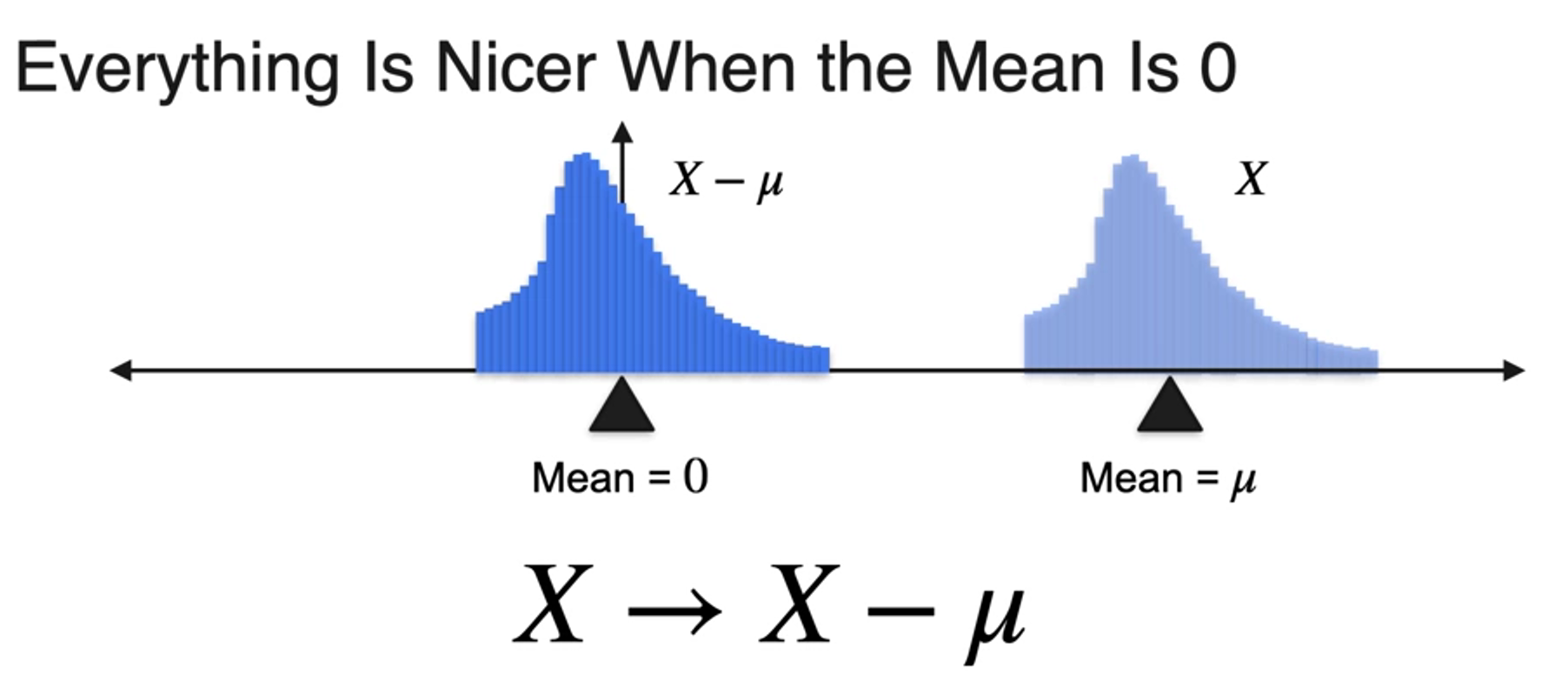
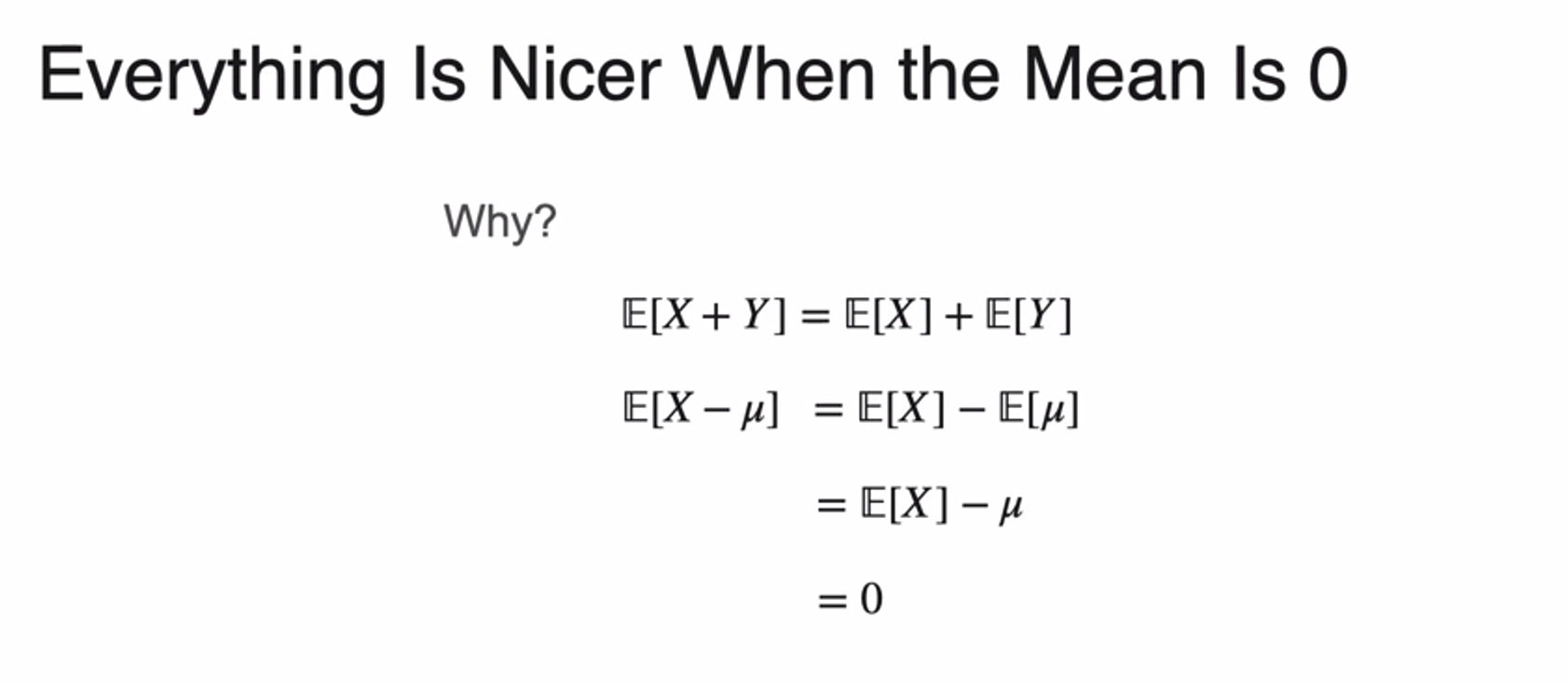
• We always prefer distribution has mean zero

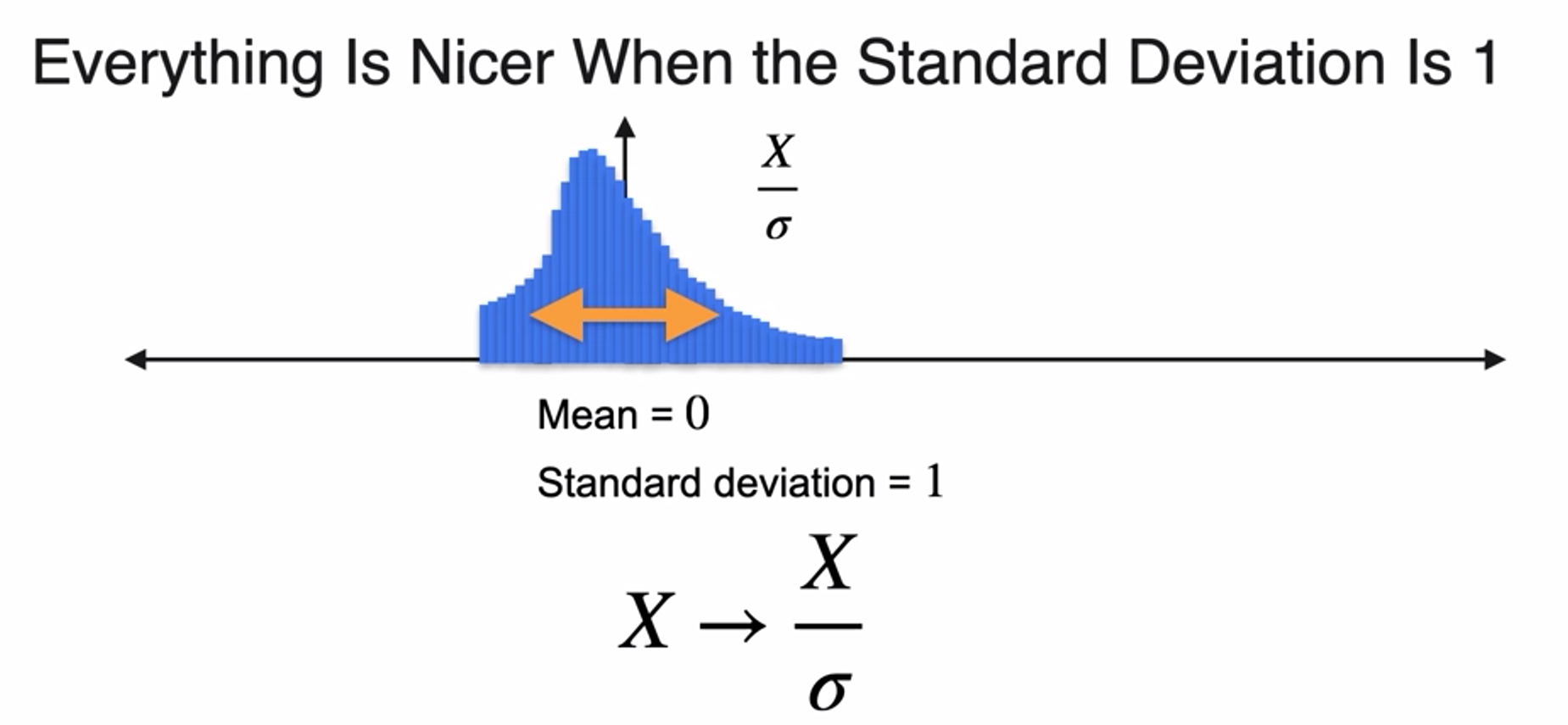
• We also prefer standard deviation to be one

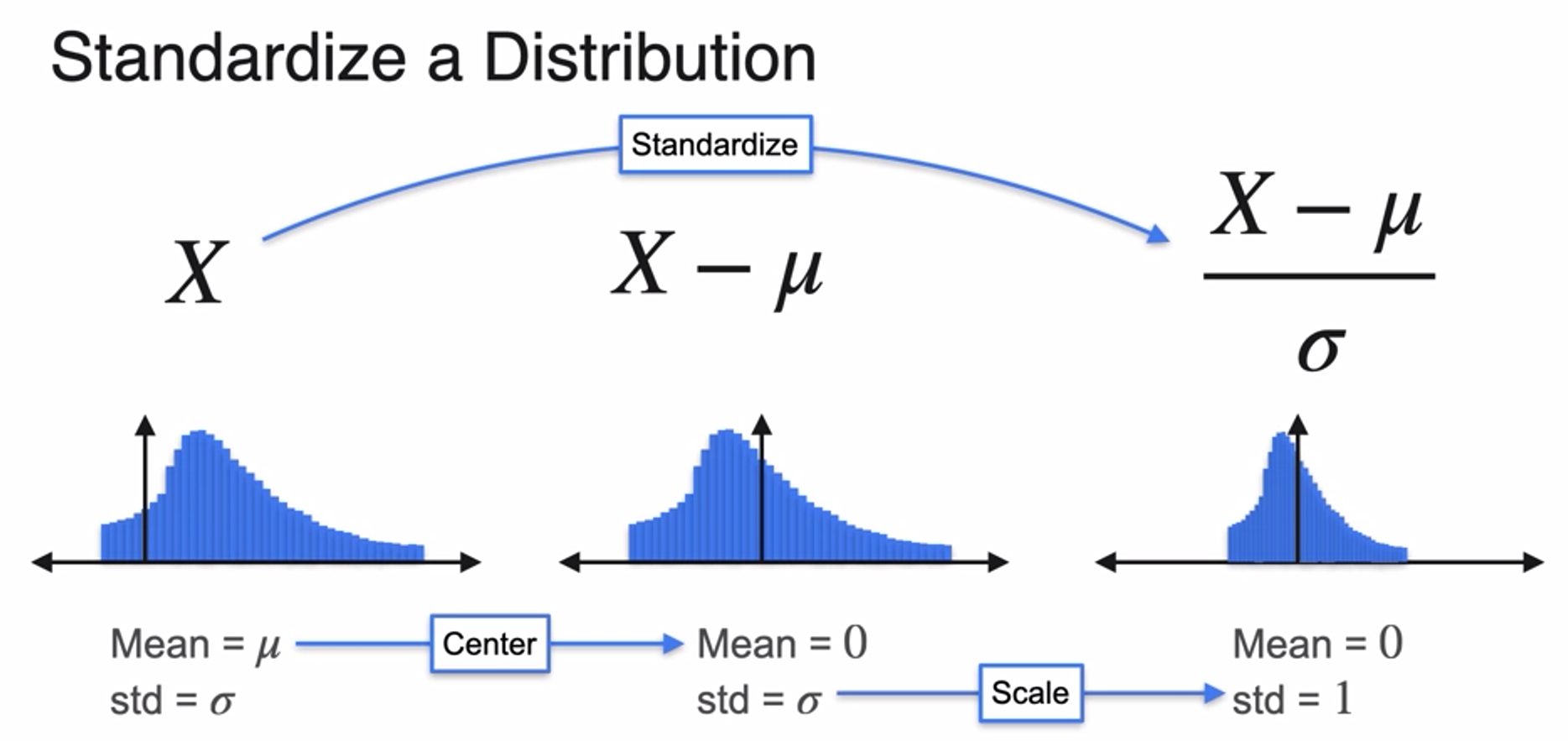
• Standardizing
  • Centering(mean to 0)
  • Scaling(std to 1)

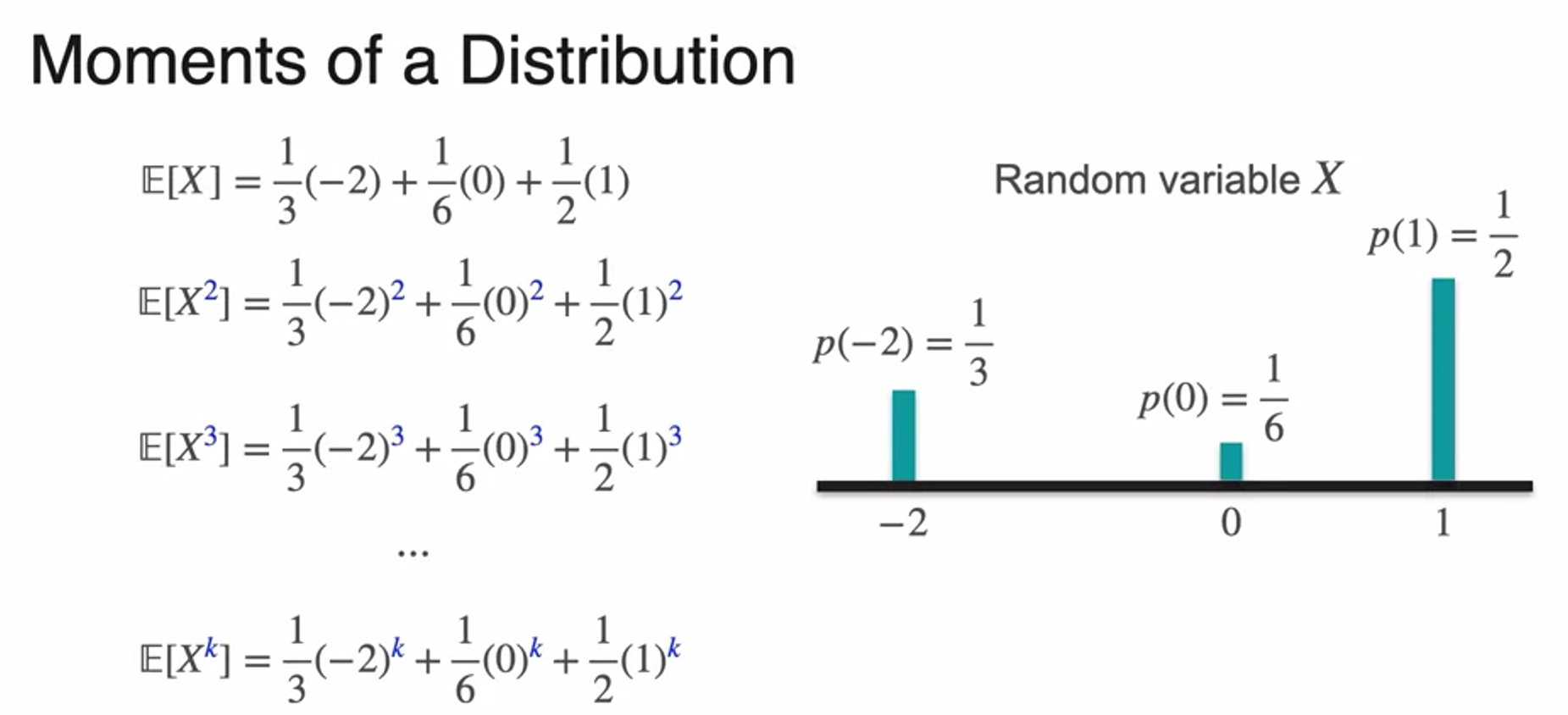
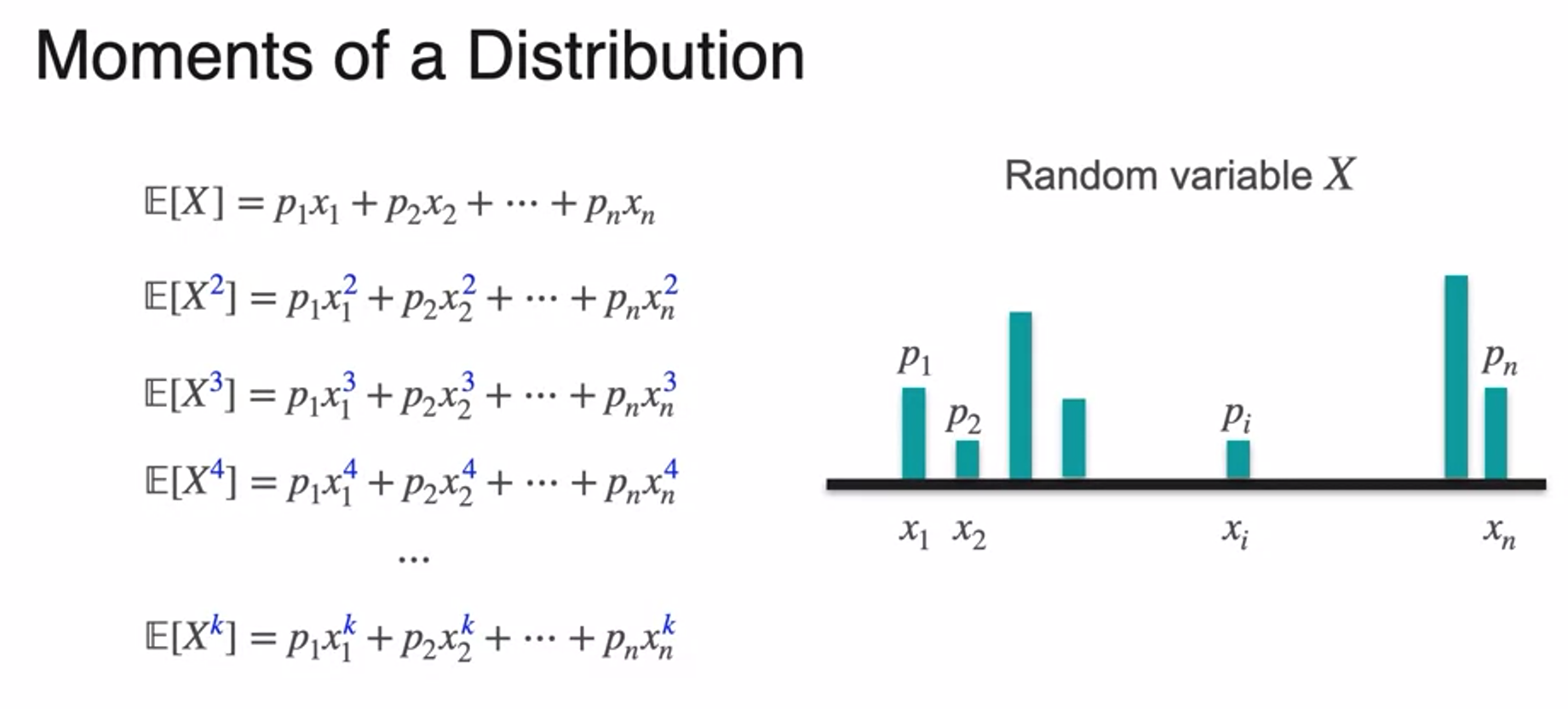
Skewness and Kurtosis: Moments of a Distribution

• 왜도와 첨도Skewness and Kurtosis
  

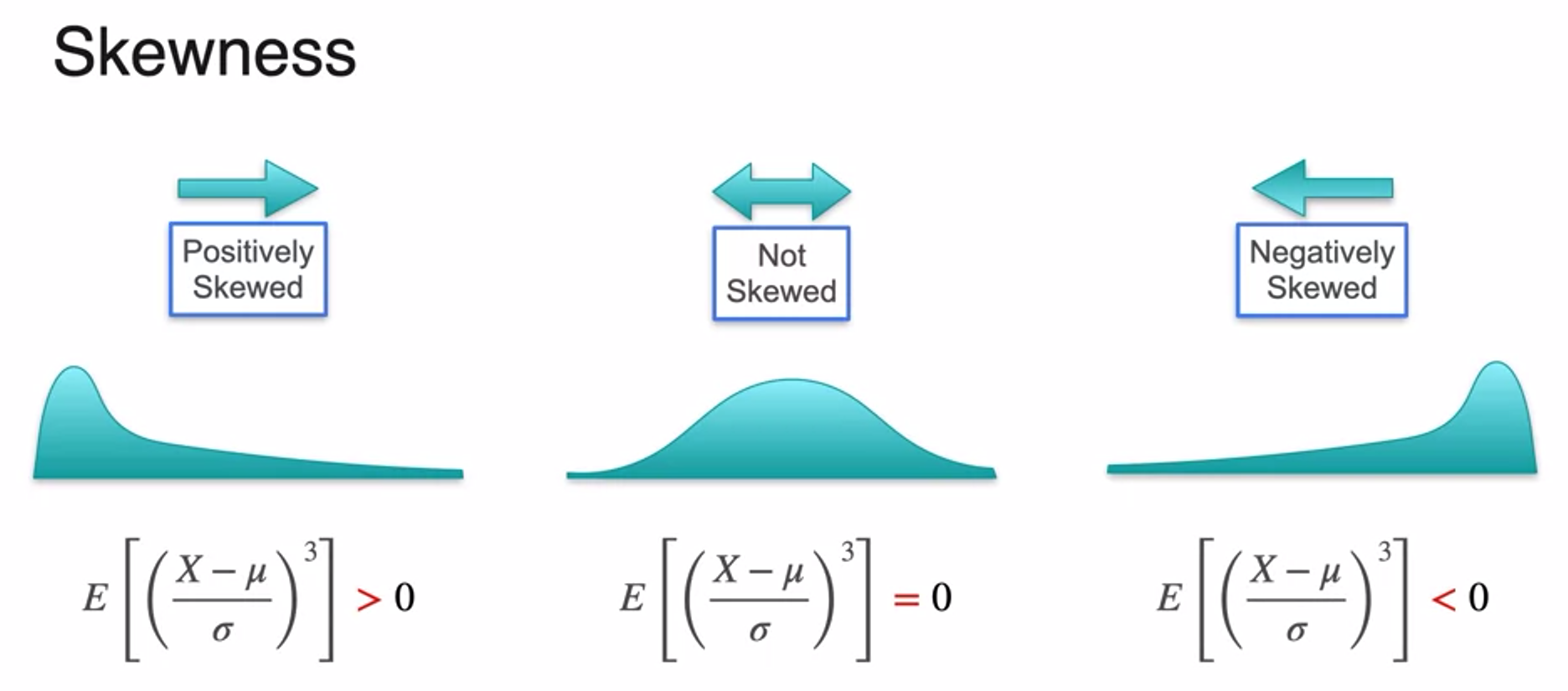
Skewness and Kurtosis - Skewness

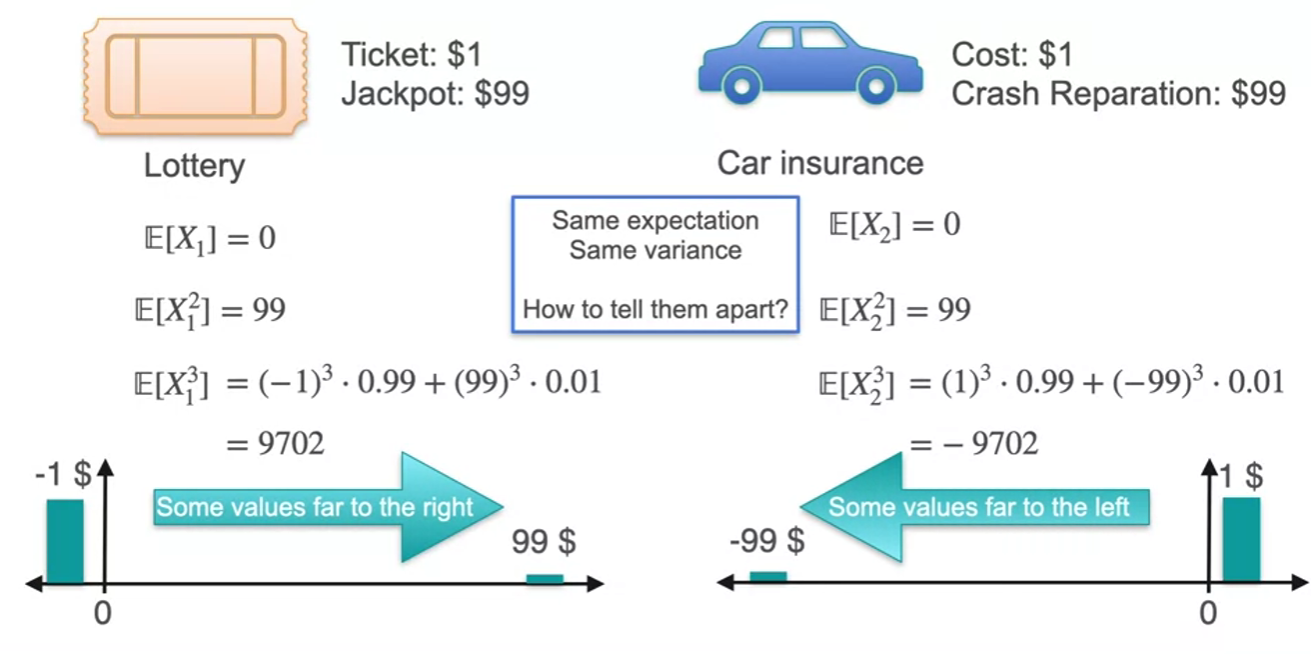
• second까지 차이가 없다면 세제곱cube를 사용

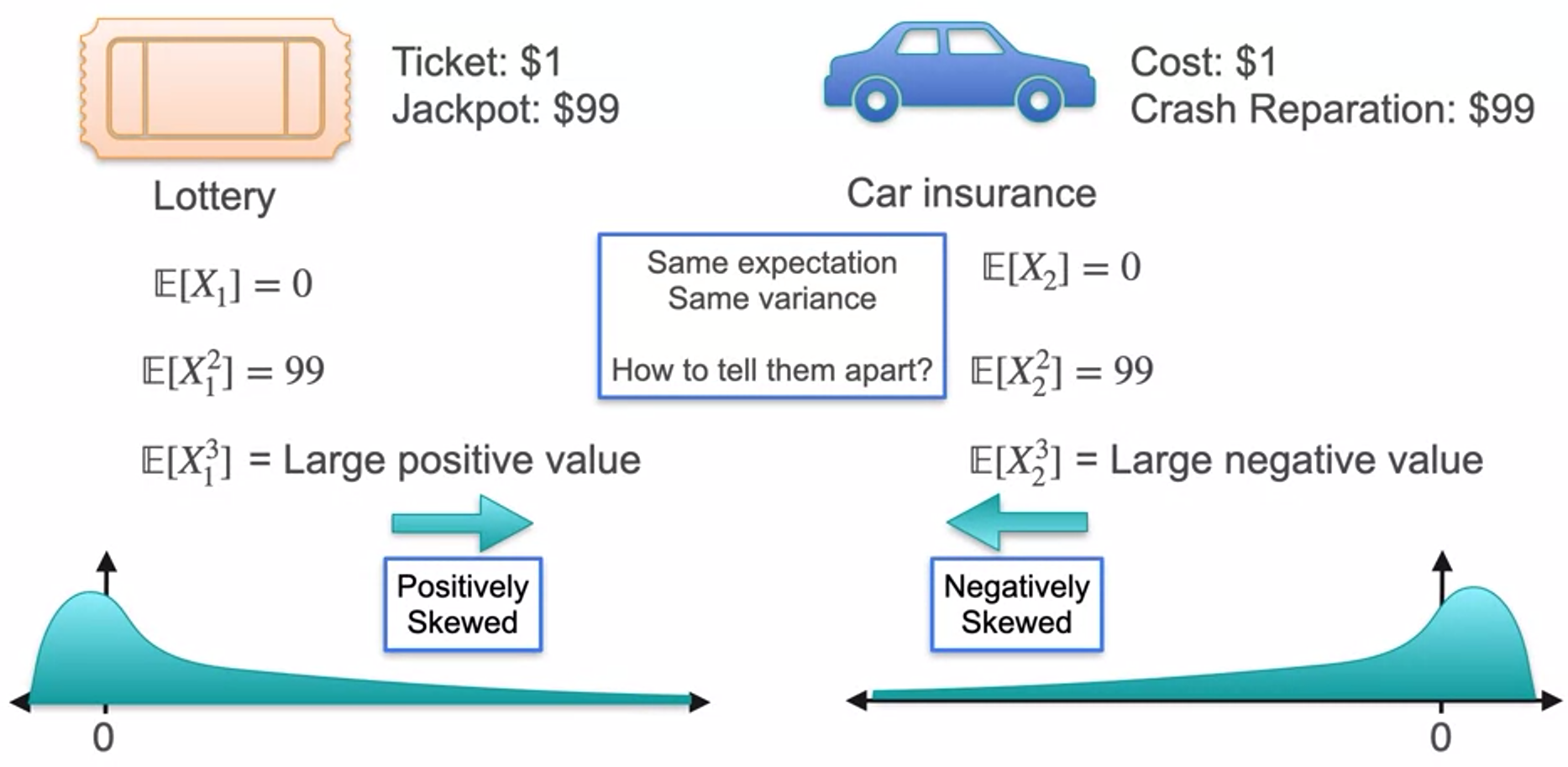
• Standardize $\mathbb{E}[X^3]$
  $\mathbb{E}[\left(\frac{X - \mu}{\sigma}\right)^3]$

• positive skewed means distribution skewed toward right and tail of the distribution extending towards the higher values on the right side

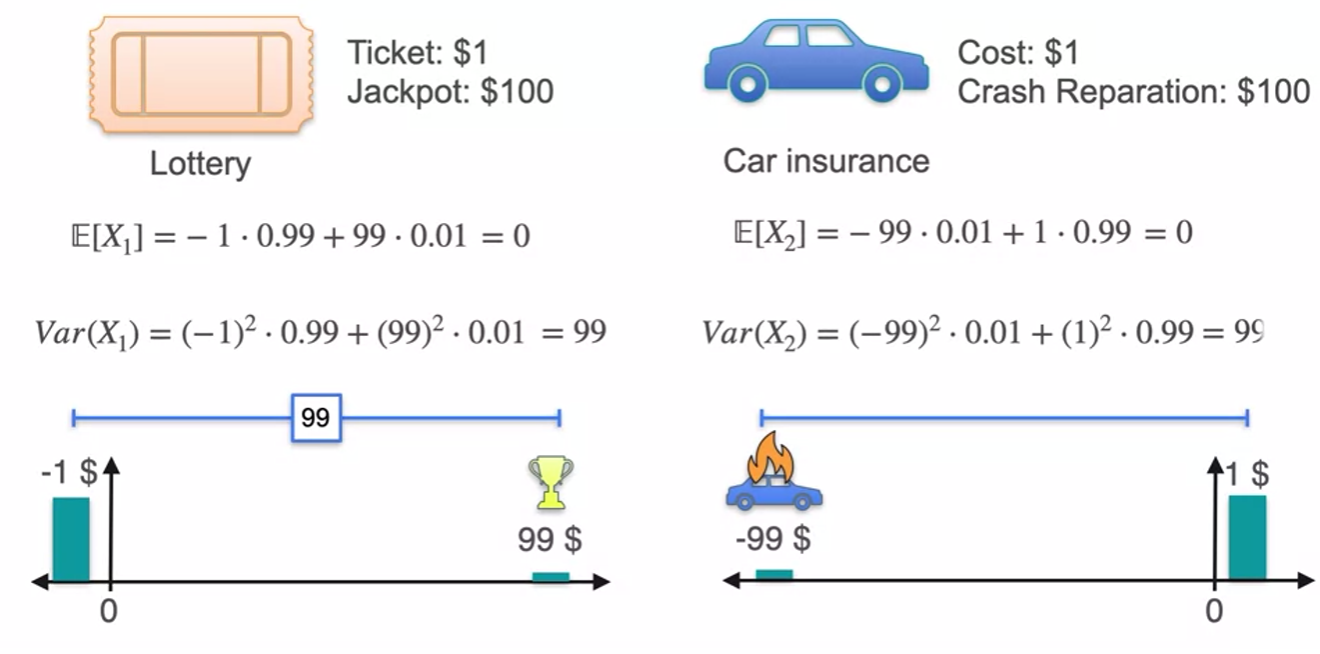
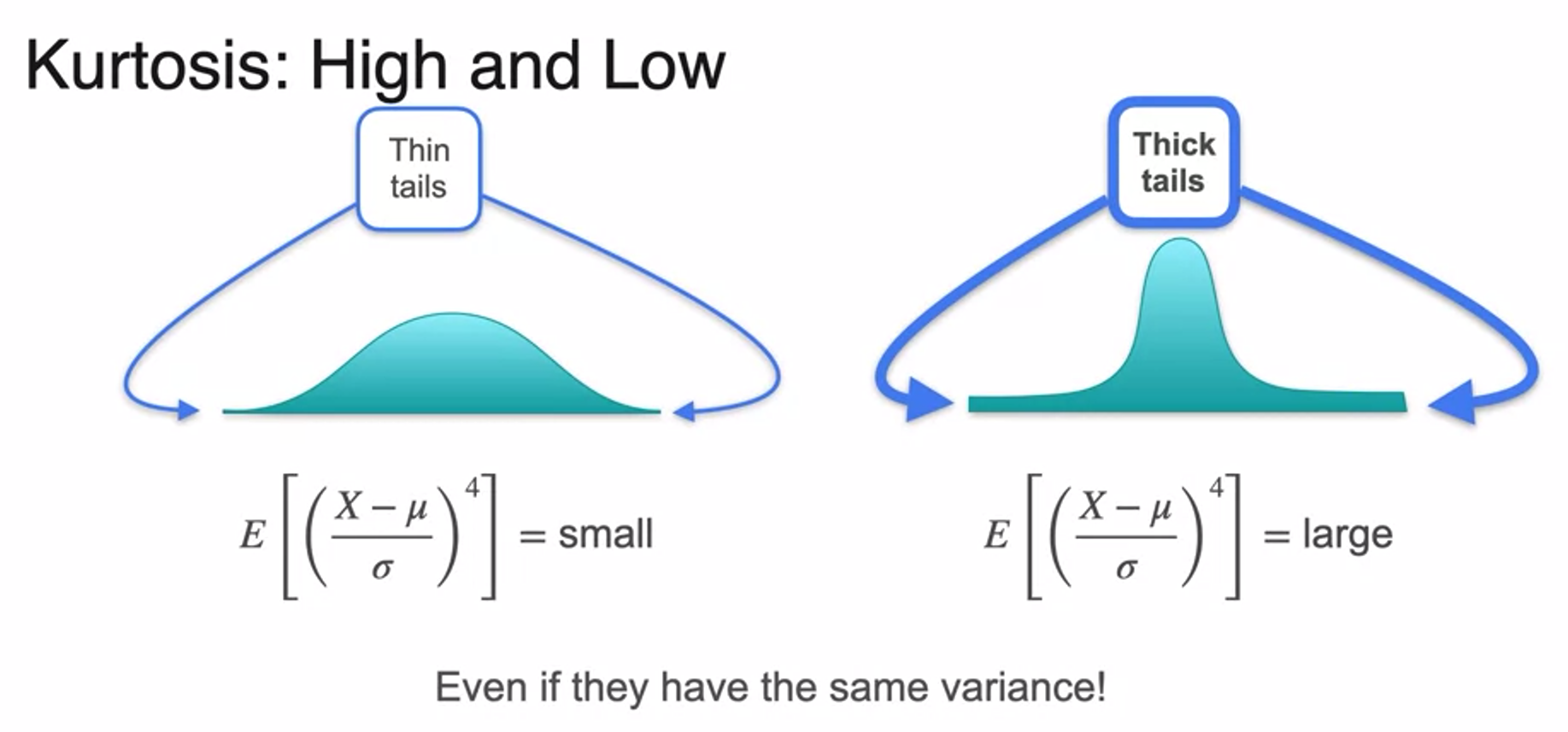
Skewness and Kurtosis - Kurtosis

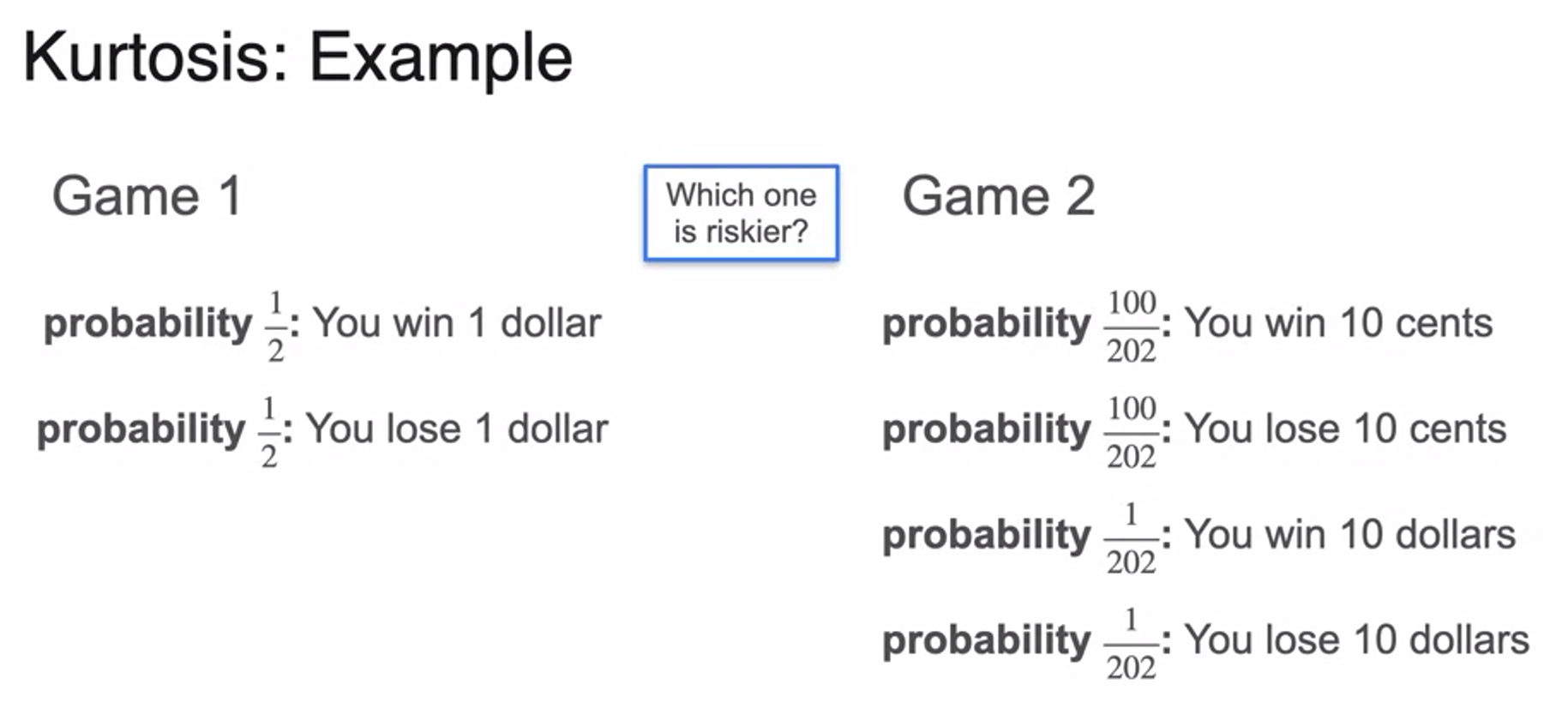
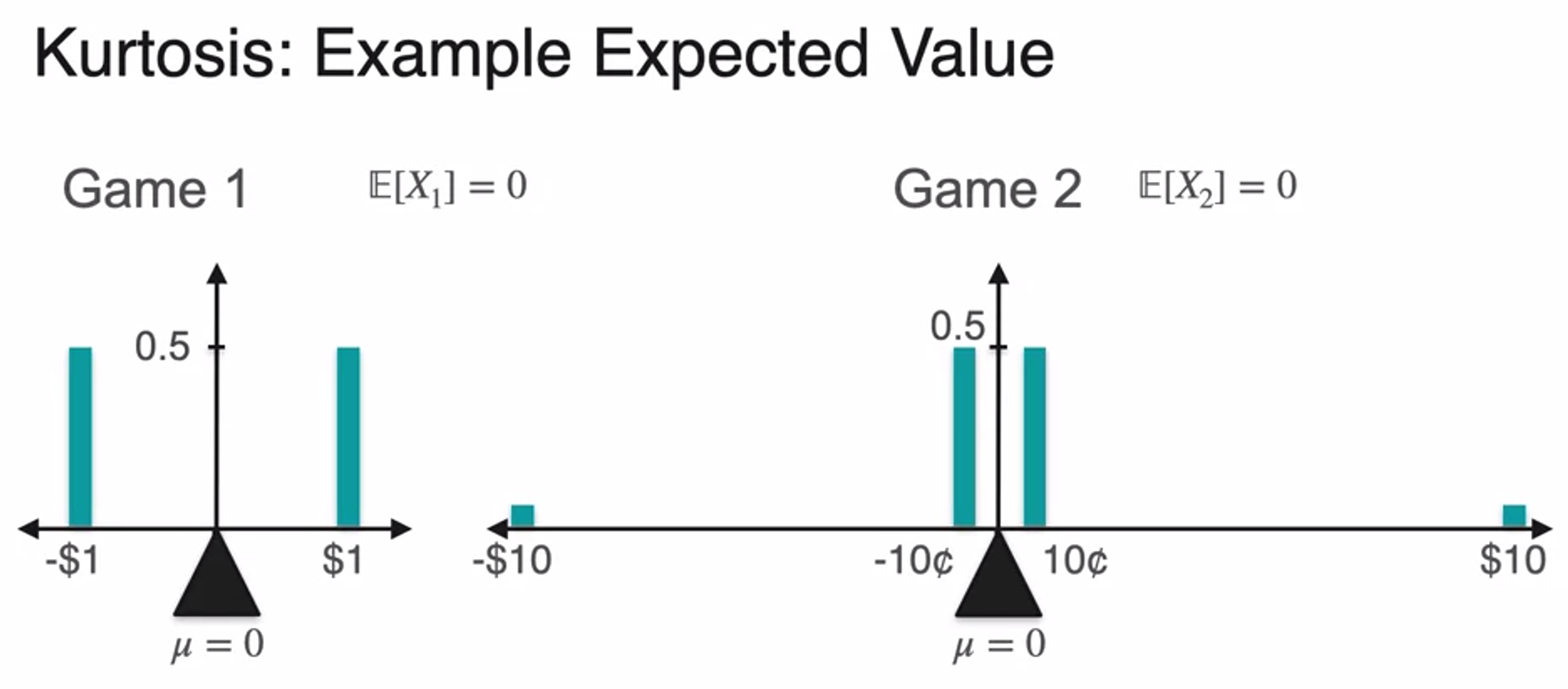
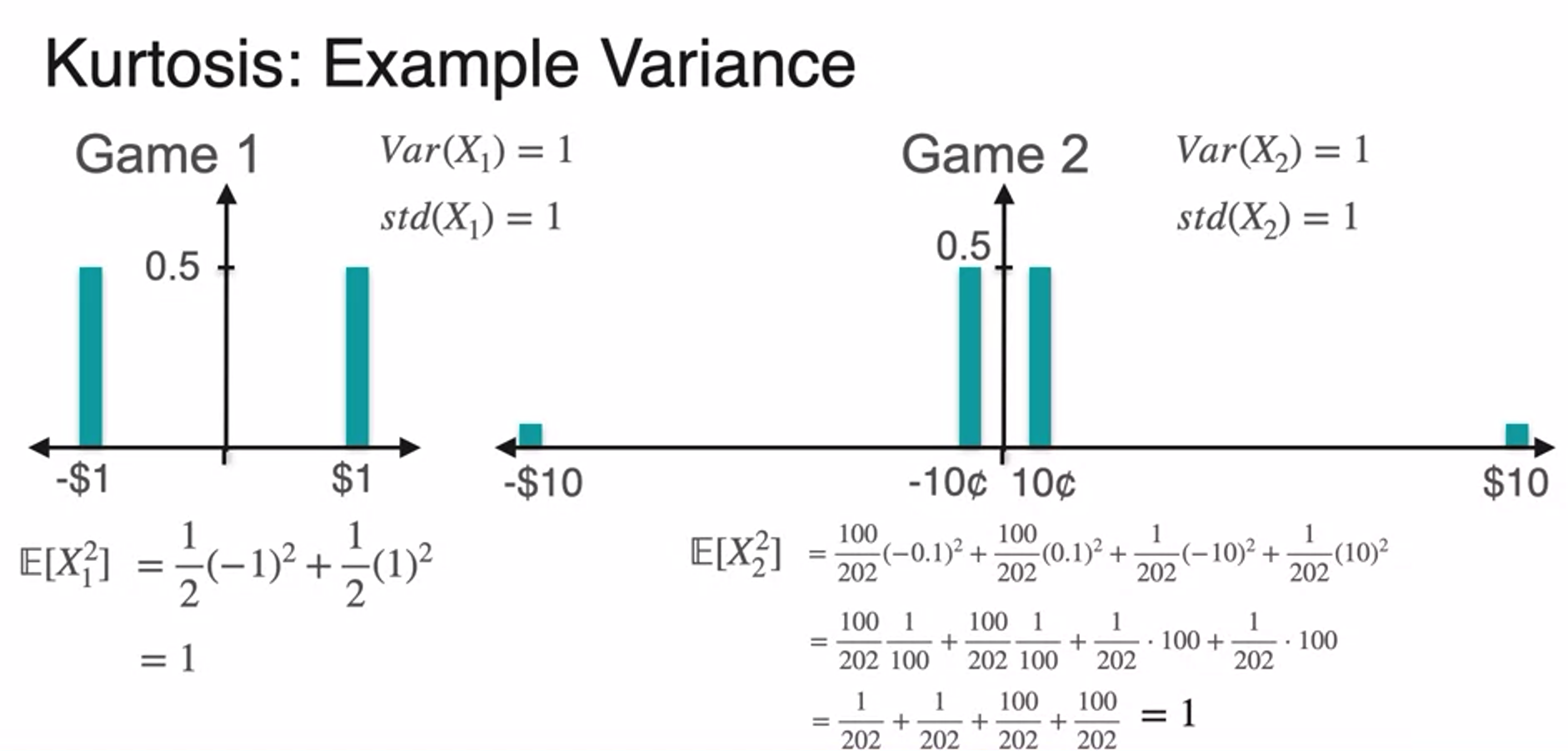
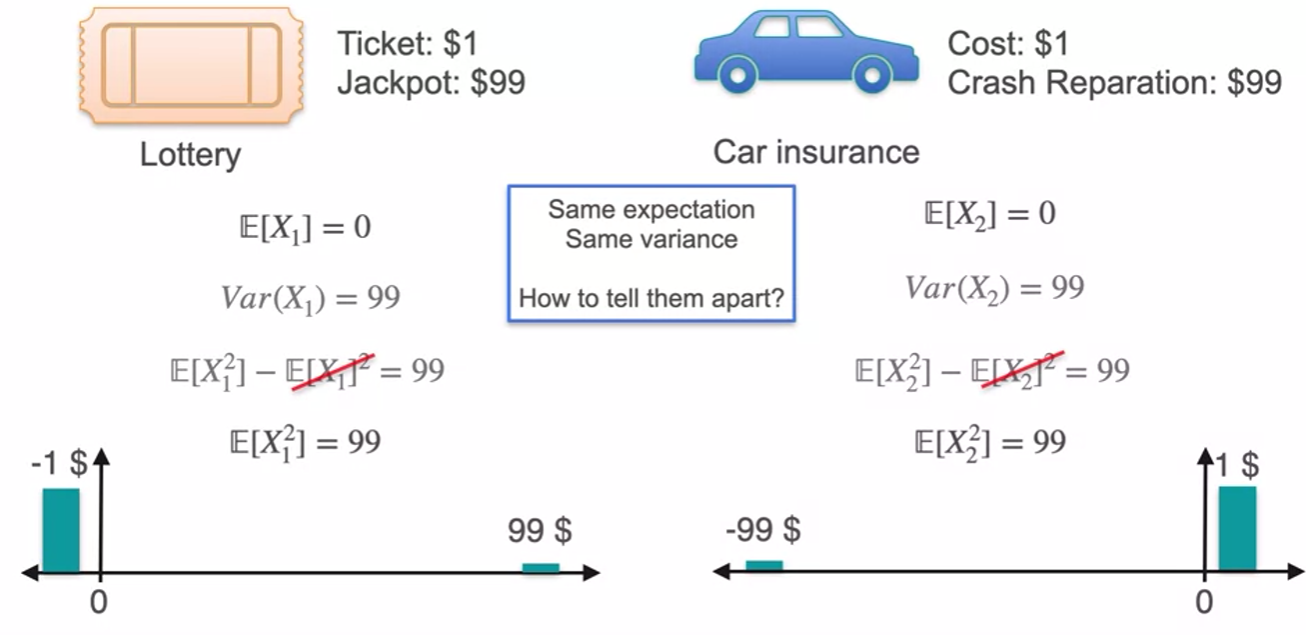
• we can't tell them apart using expected value and variance

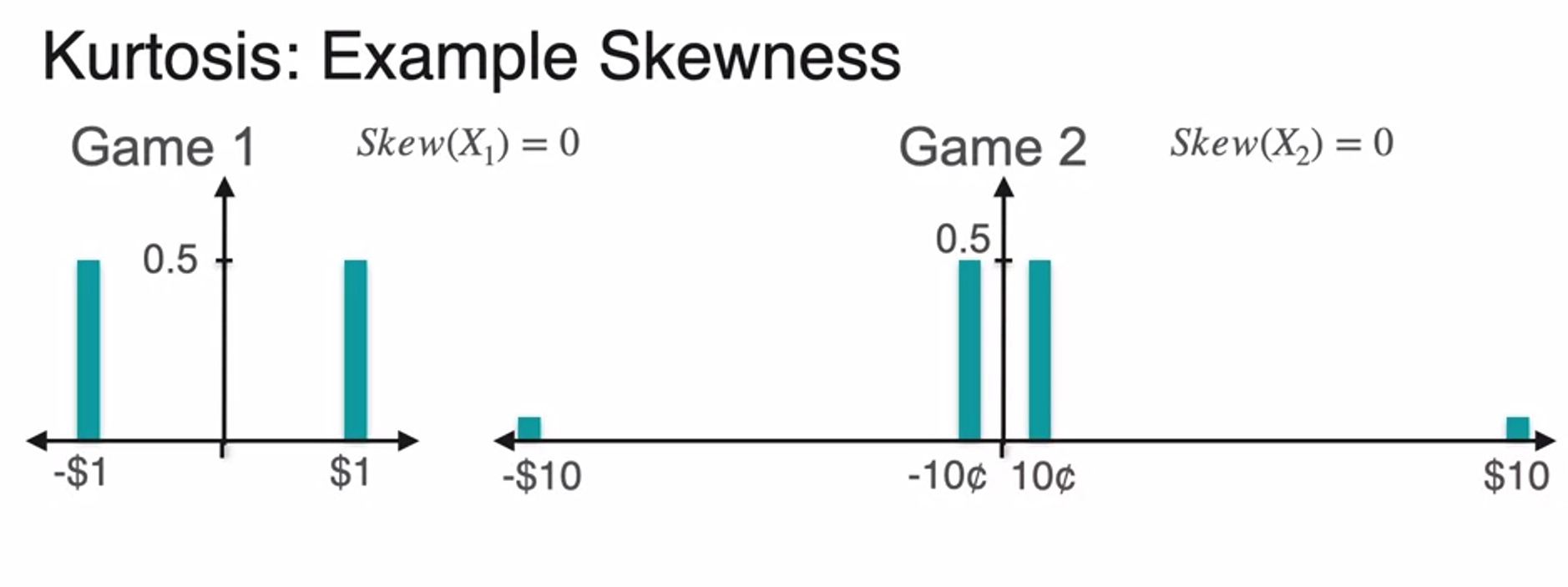
• distribution symmetric around midpoint skeness is 0

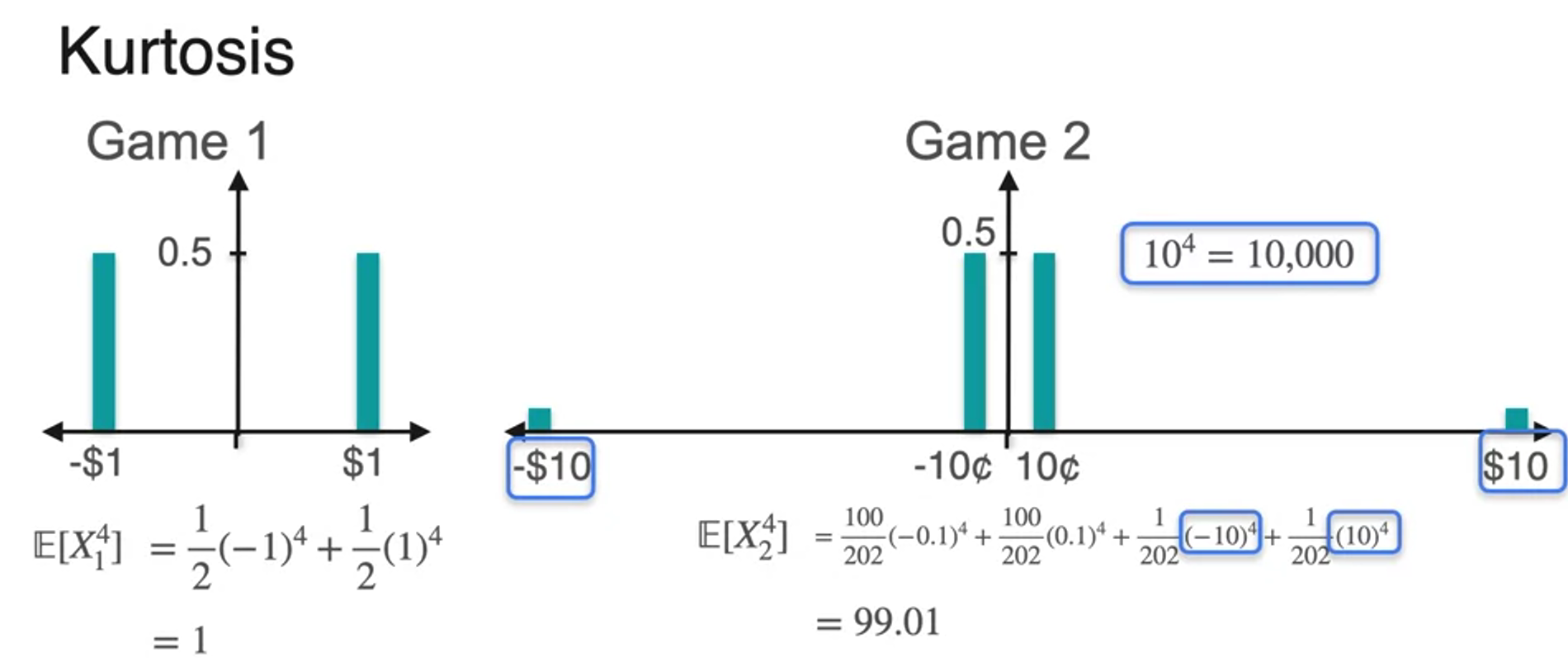
• 4th moment can figure this
• this is kurtosis

• Standardize $\mathbb{E}[X^4]$
  $\mathbb{E}[\left(\frac{X - \mu}{\sigma}\right)^4]$

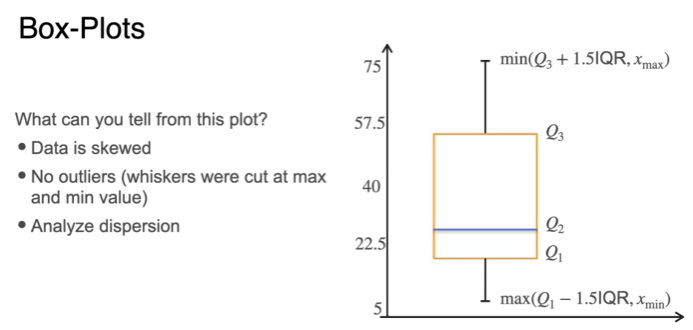
Quantiles and Box-Plots

• what is quartile

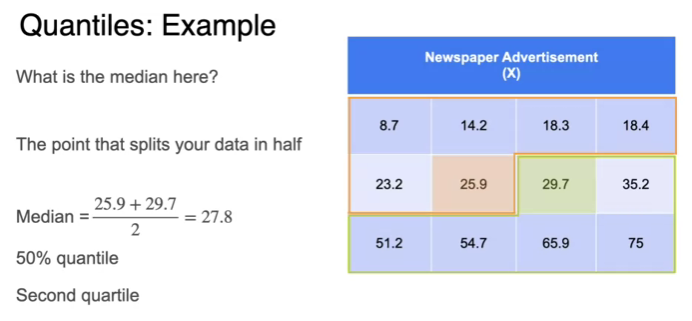
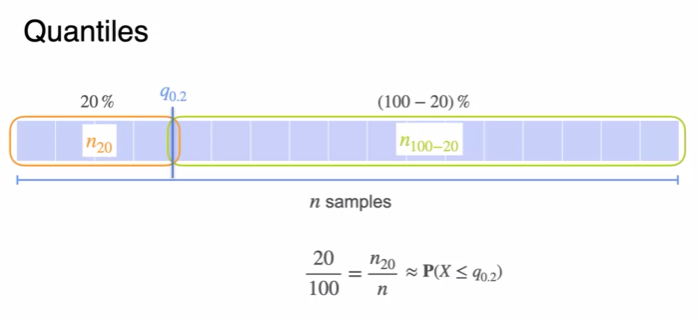
• probability variable X that I measured is below k percentage quantile

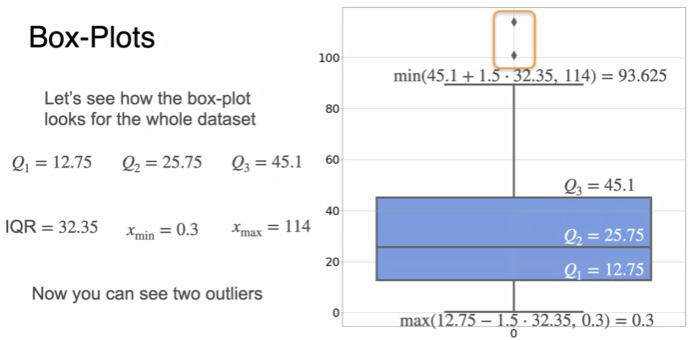
Visualizing data: Box-Plots

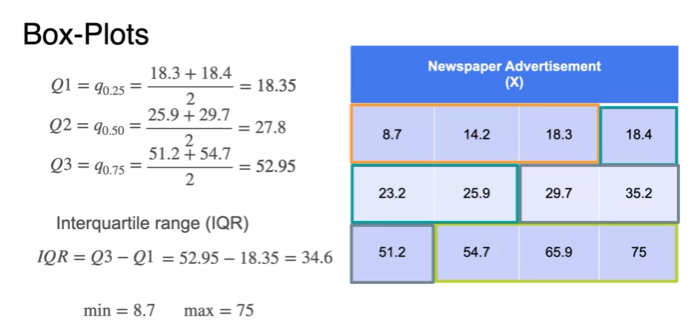
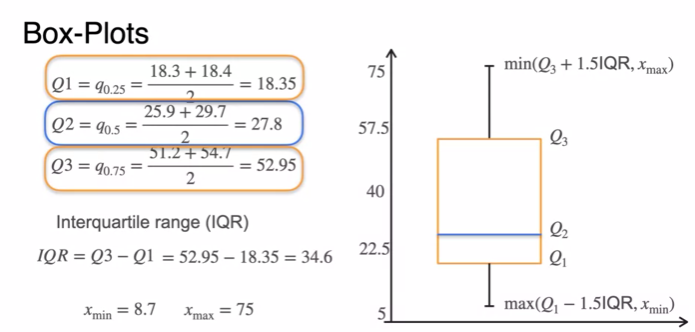
• draw whiskers
  IQR = interquartile
  $max(Q_1-1.5IQR, x_{max})$
  $min(Q_3+1.5IQR, x_{min})$
  

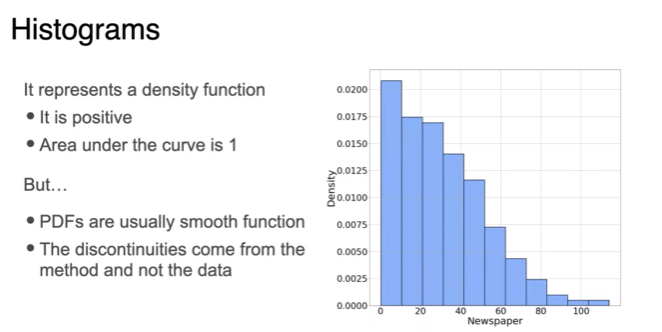
Visualizing data: Kernel density estimation

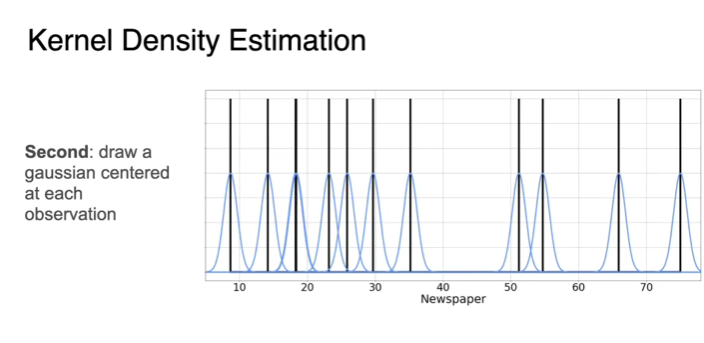
• Gaussian curve for each data point = kernal
• sigma I choose for Gaussian density will determine how far the effect of each point spreads

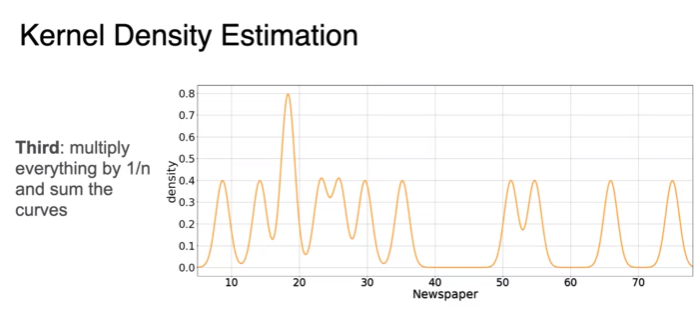
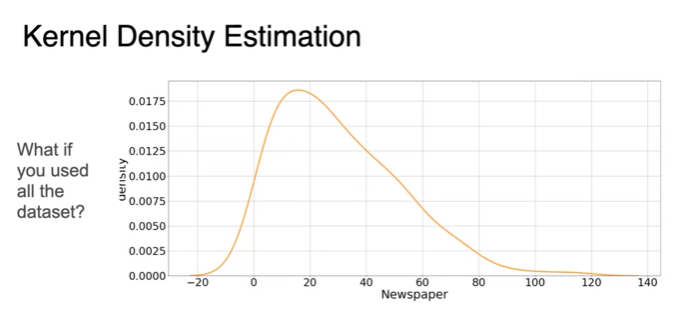
• This is a way to approximate the PDF based on the data

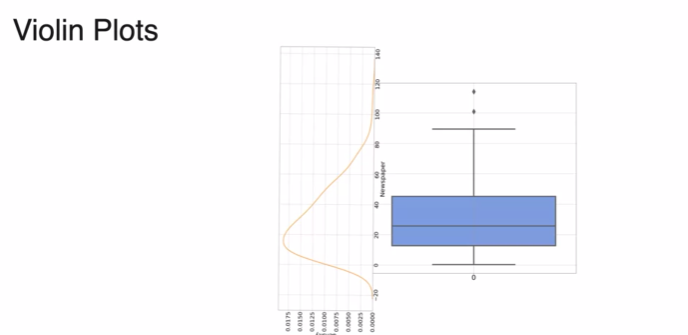
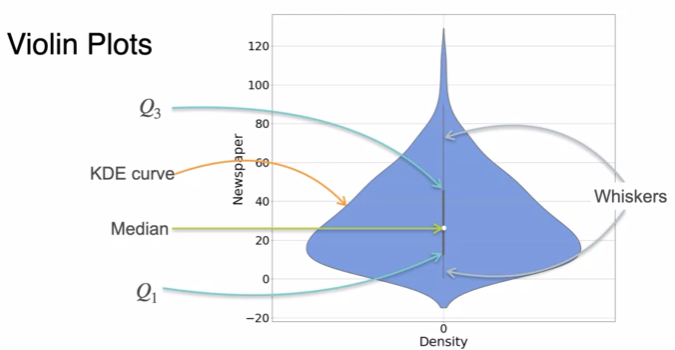
Visualizing data: Violin Plots

Visualizing data: QQ plots

• when it looks like bell shaped like the right one
• QQ plots

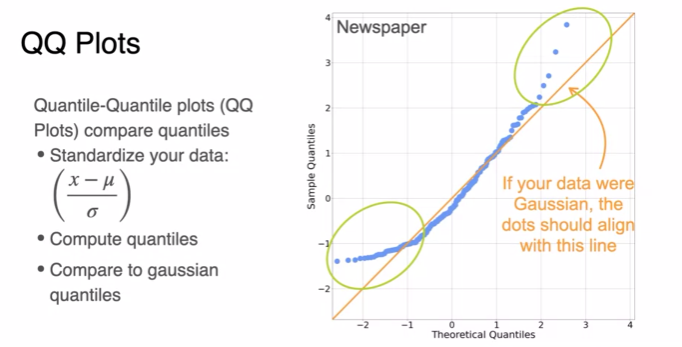
• data is more focused to left = skewed

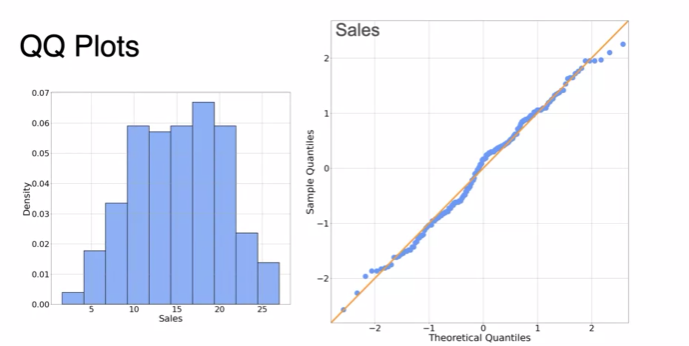
• quantiles are pretty much aligned around the orange line, which suggests a Gaussian distribution for the data

Joint Distribution (Discrete) - Part 1

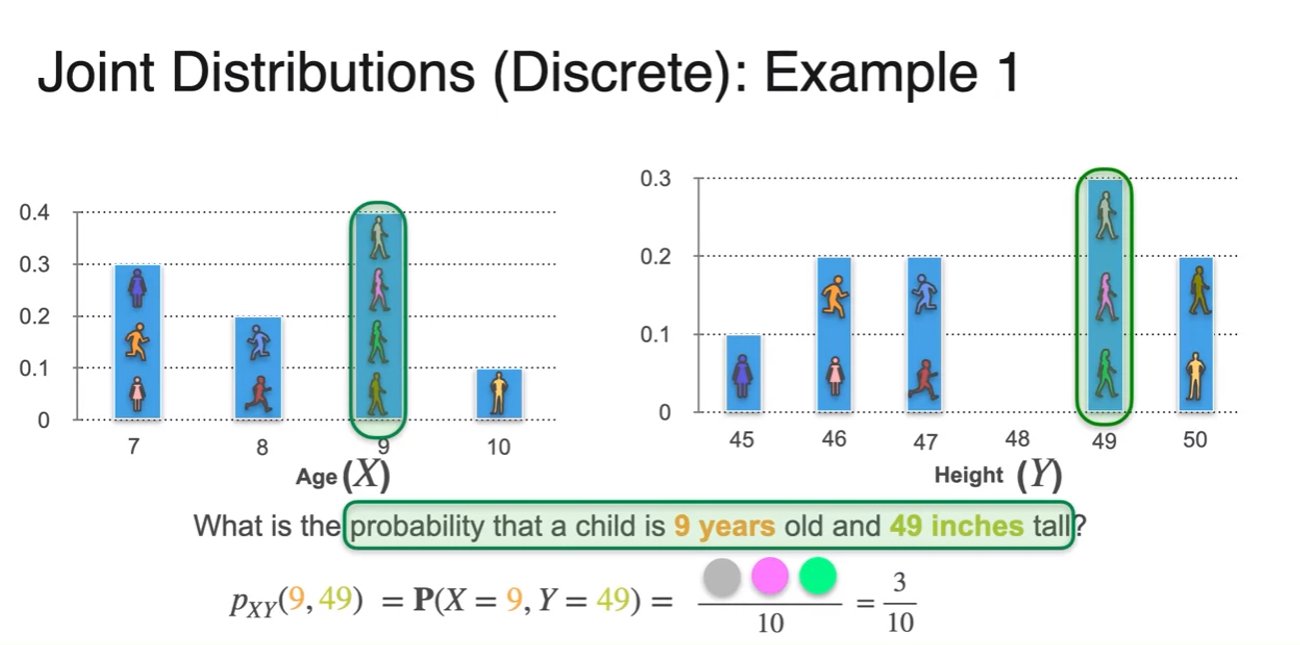
• if we organize data properly it becomes easier

• Joint Distribution 결합 분포

Joint Distribution (Discrete) - Part 2

• Independent case

• joint probability function

Joint Distribution (Continuous)

• what about jointly countinuous distribution

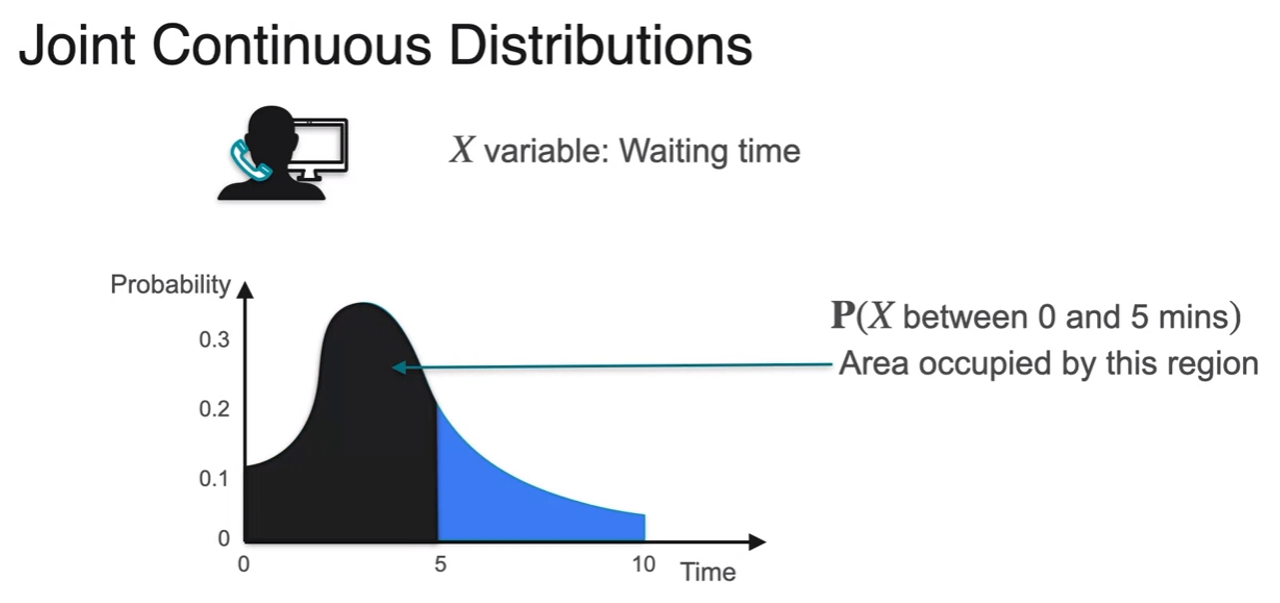
• reminder : we did this

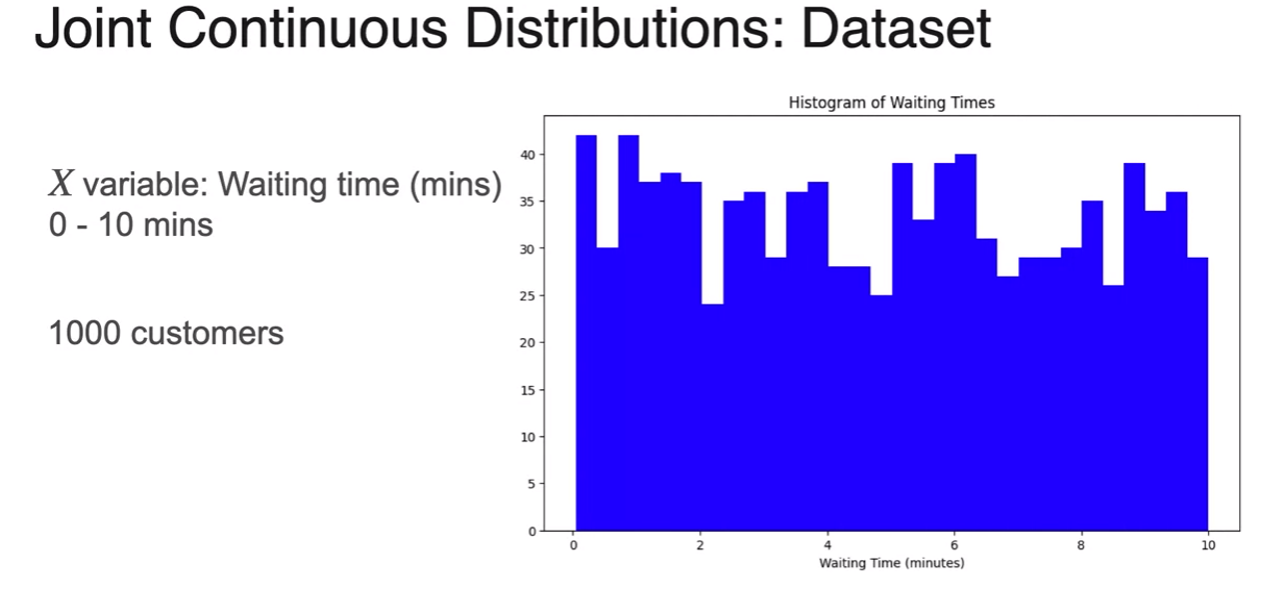
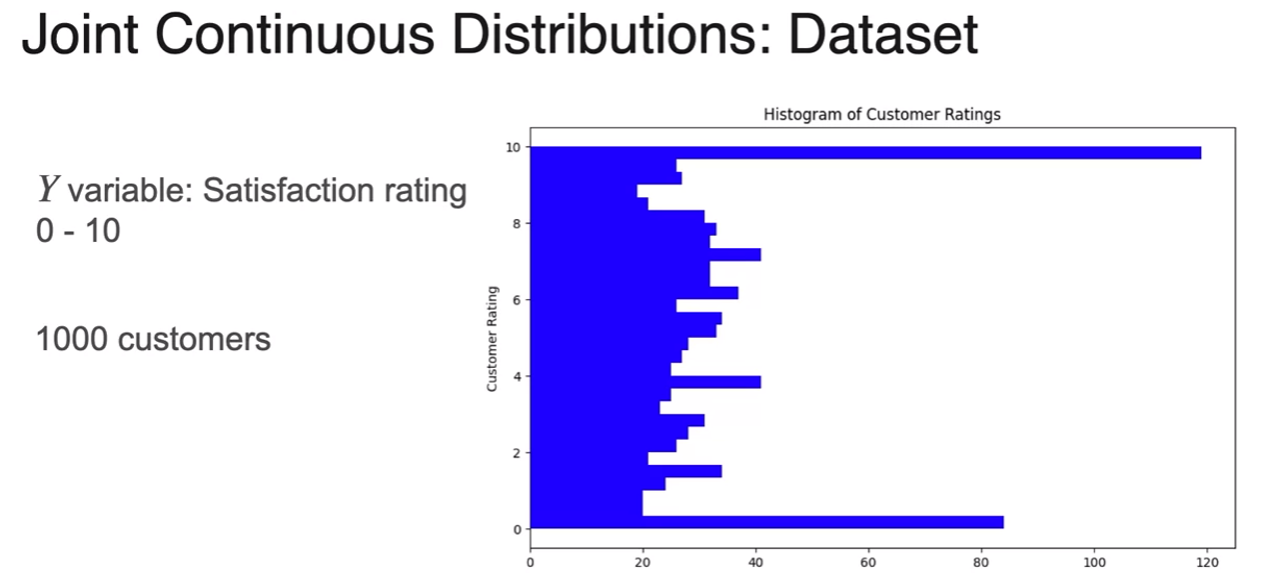
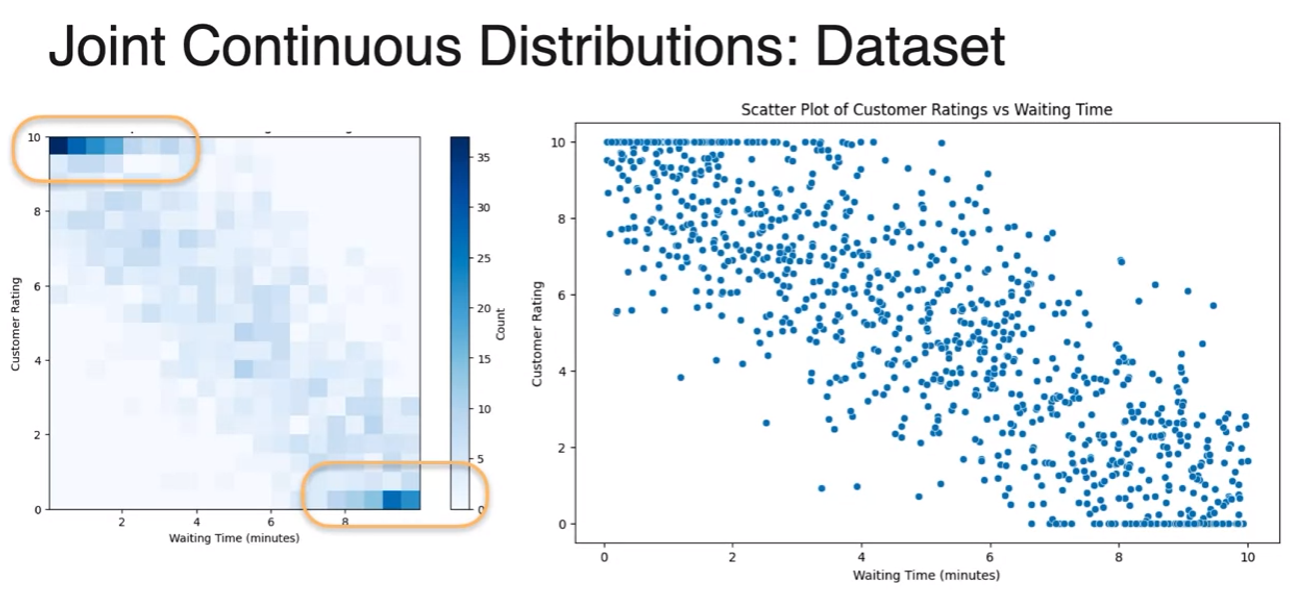
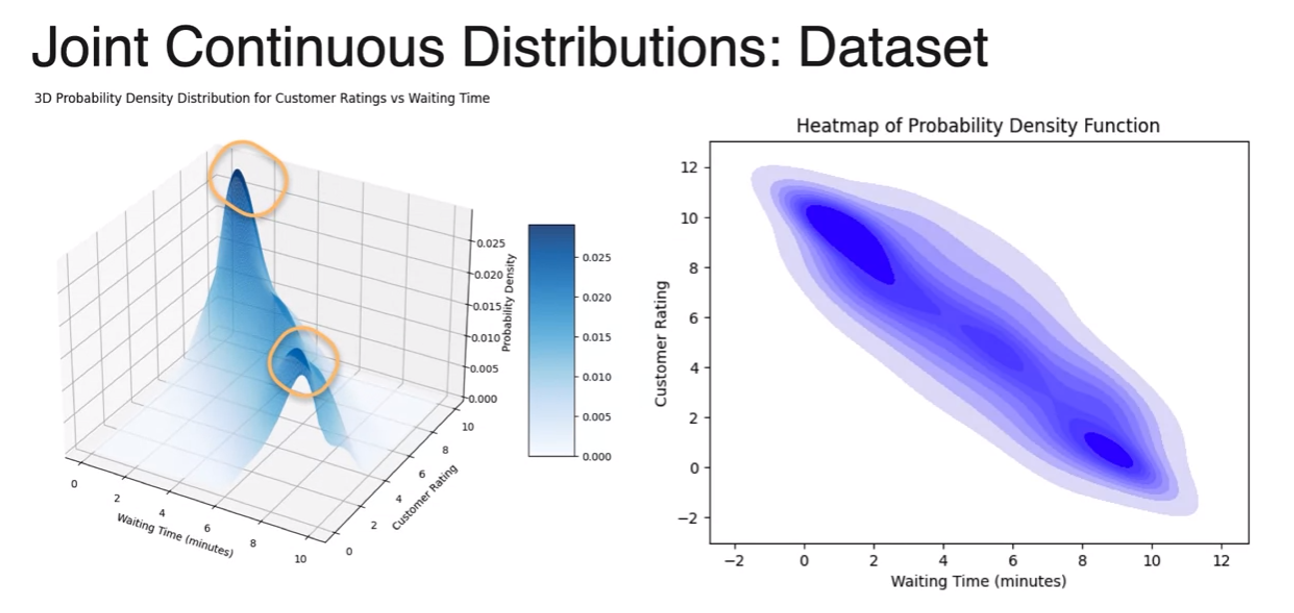
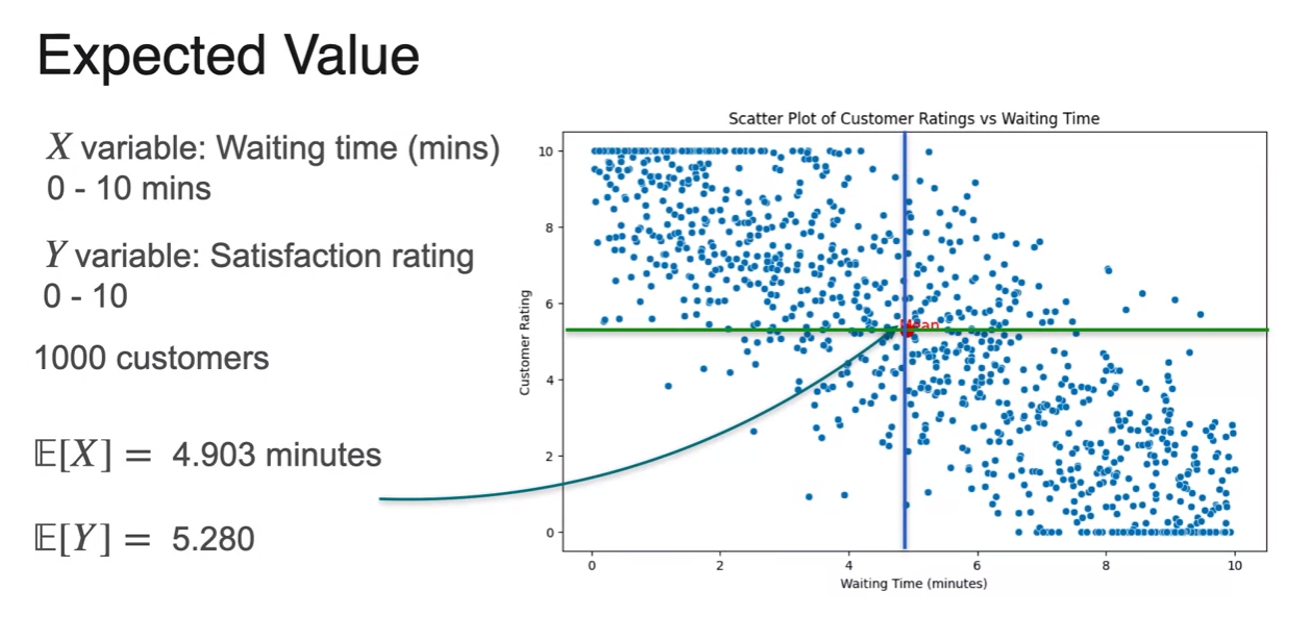
• here is mean

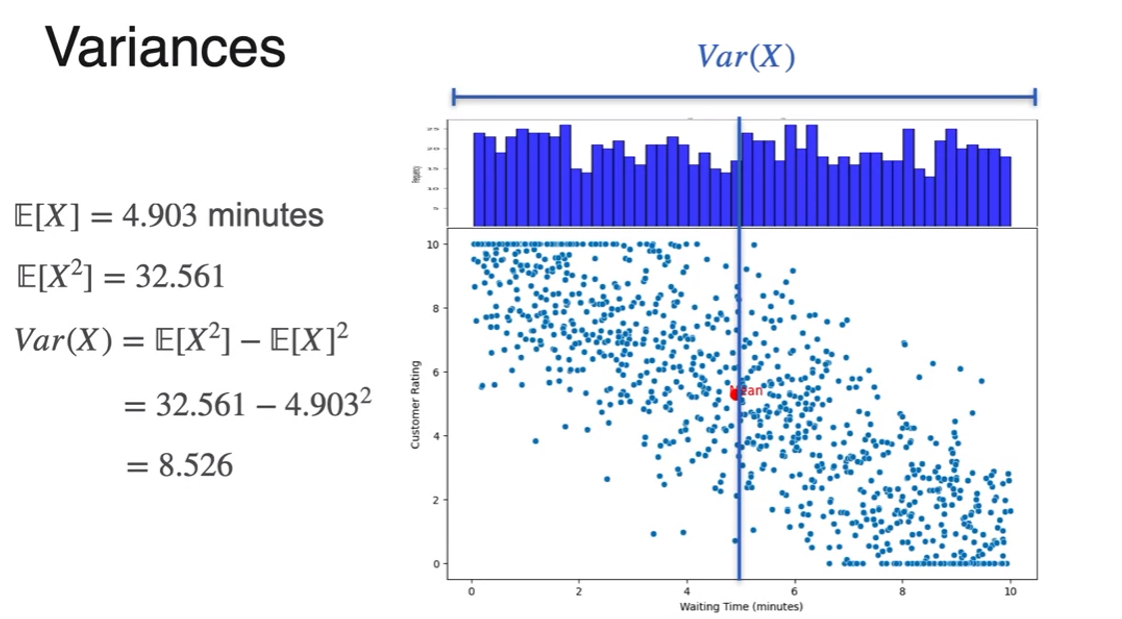
• 표준편차 제평마평제

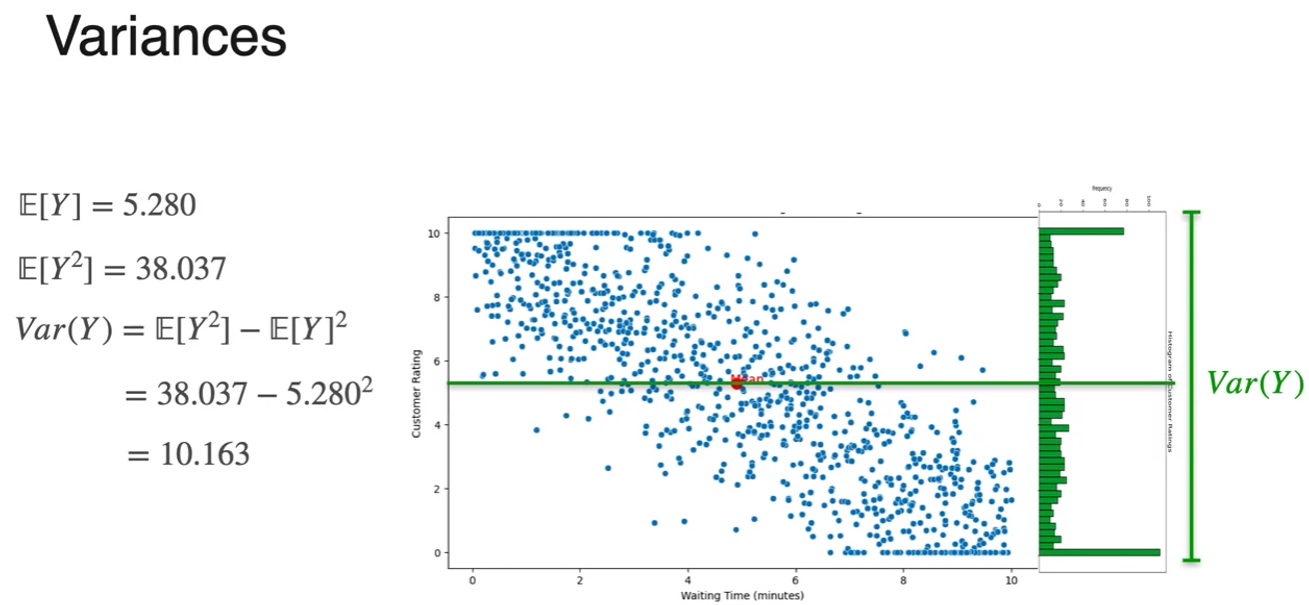
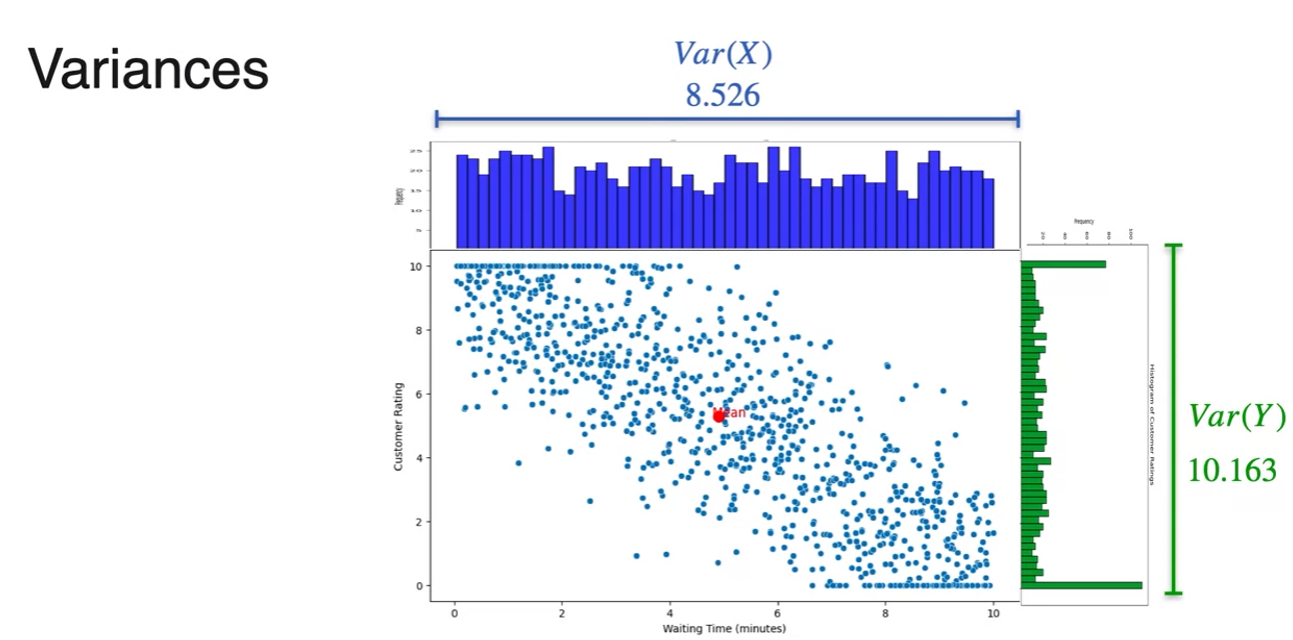
Marginal and Conditional Distribution

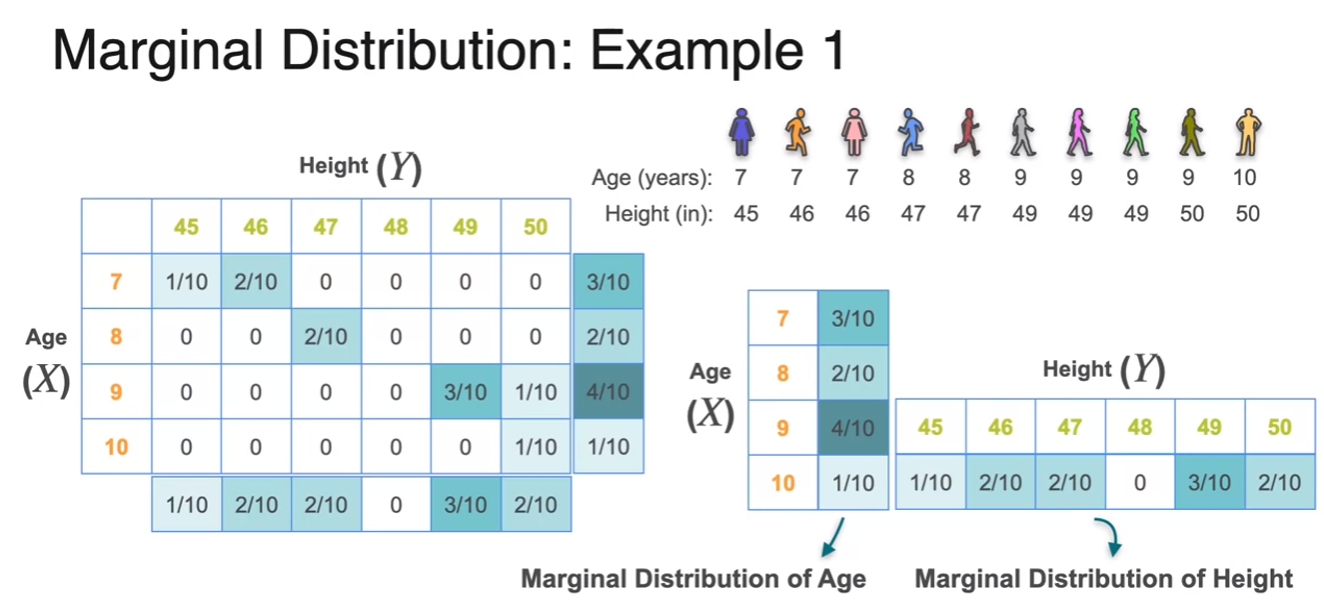
• simple case : two dice

• complicated case : sum of two dice

• goal of marginal distribution is reduce higly dimensional distribution

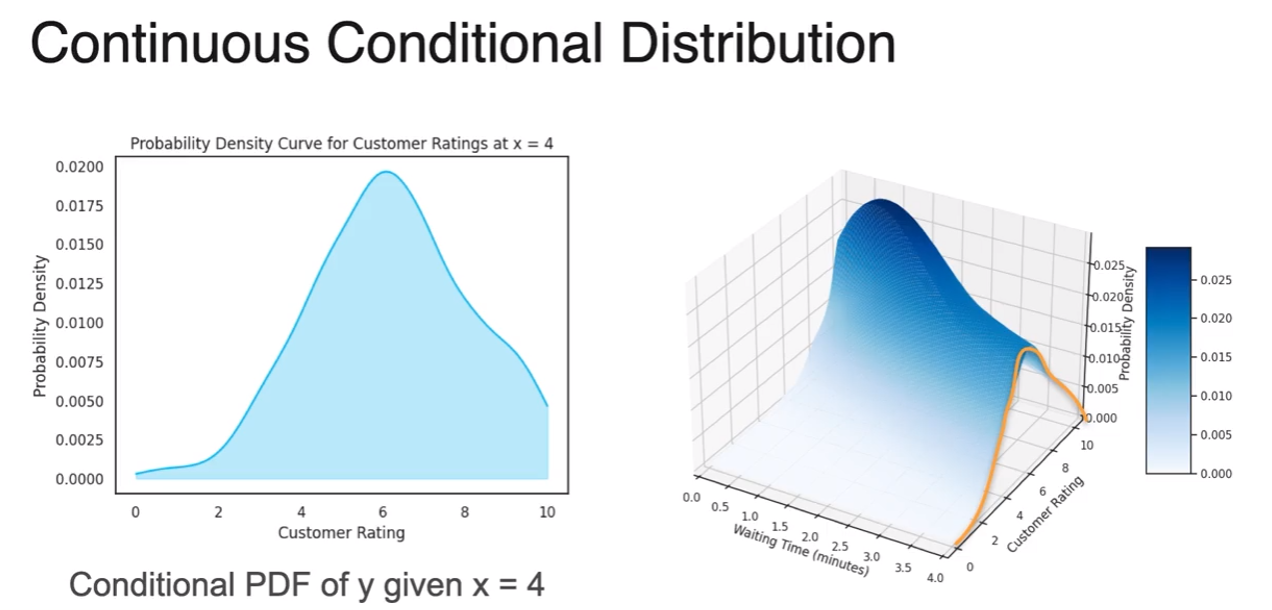
Conditional Distribution

• what if we want something different

• caveat 경고

Covariance of a Dataset

• 공분산

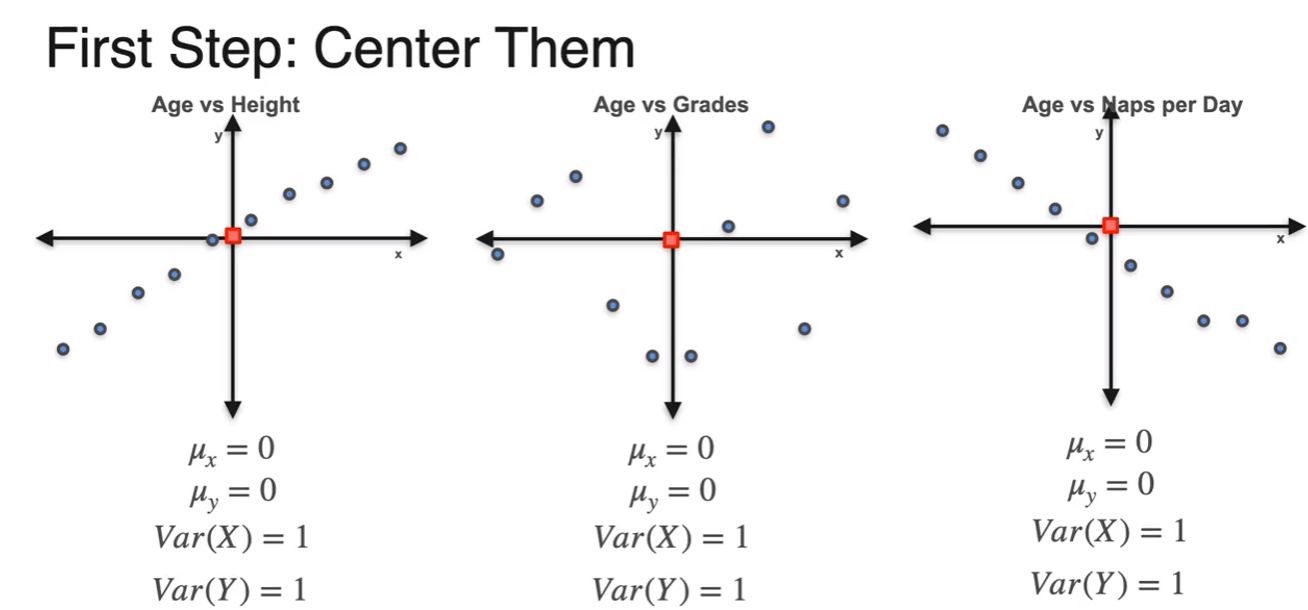
• generate scatter plots

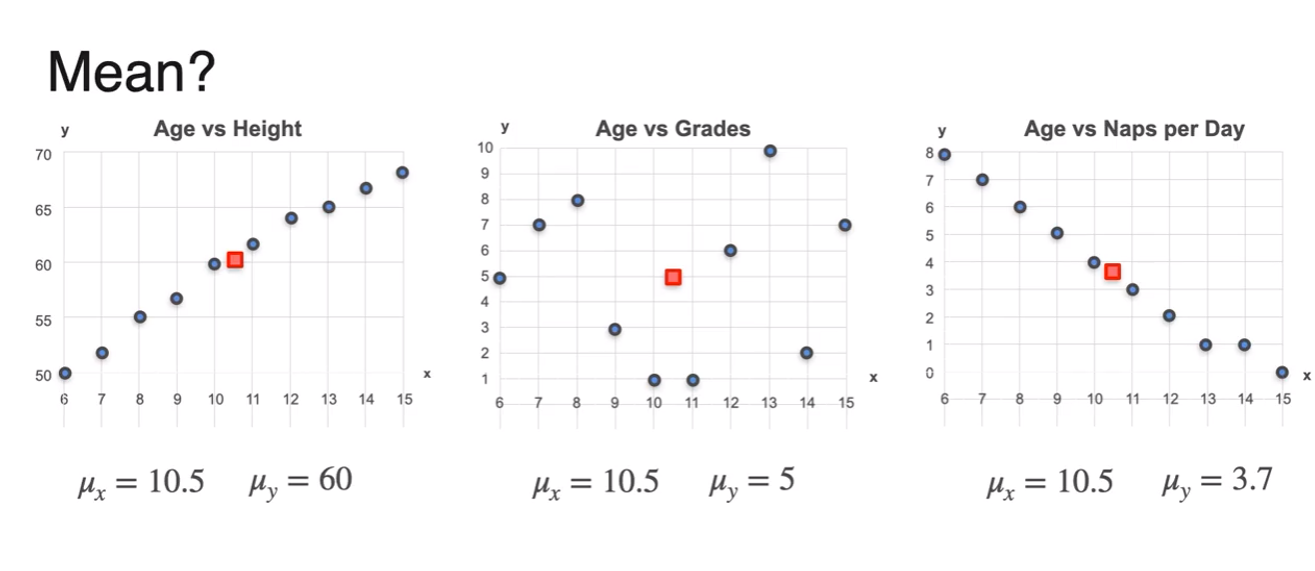
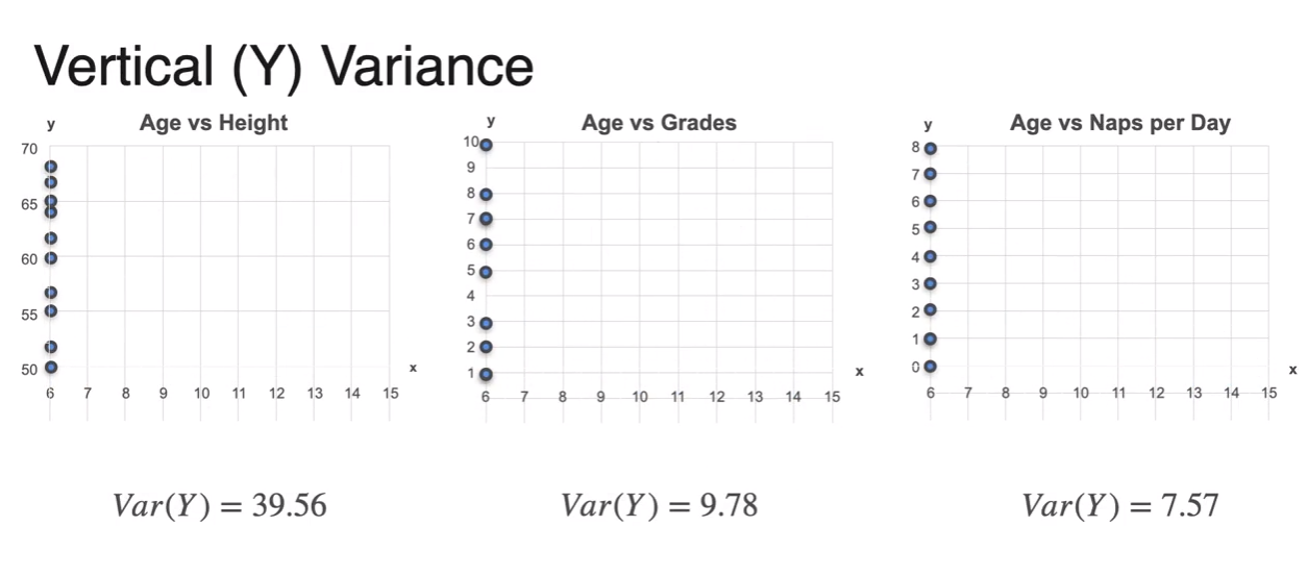
• each of means and variances

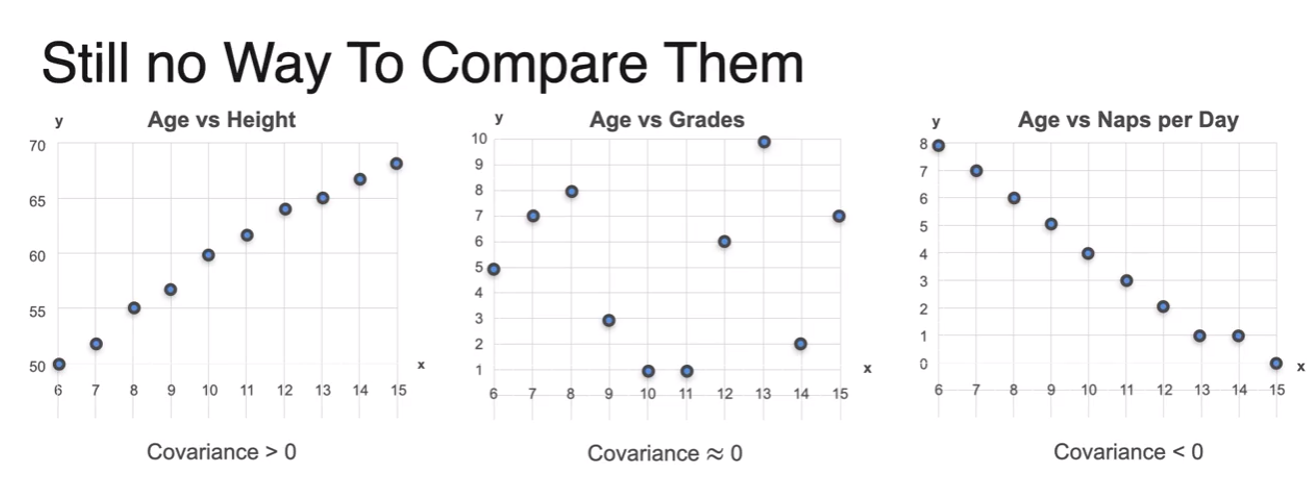
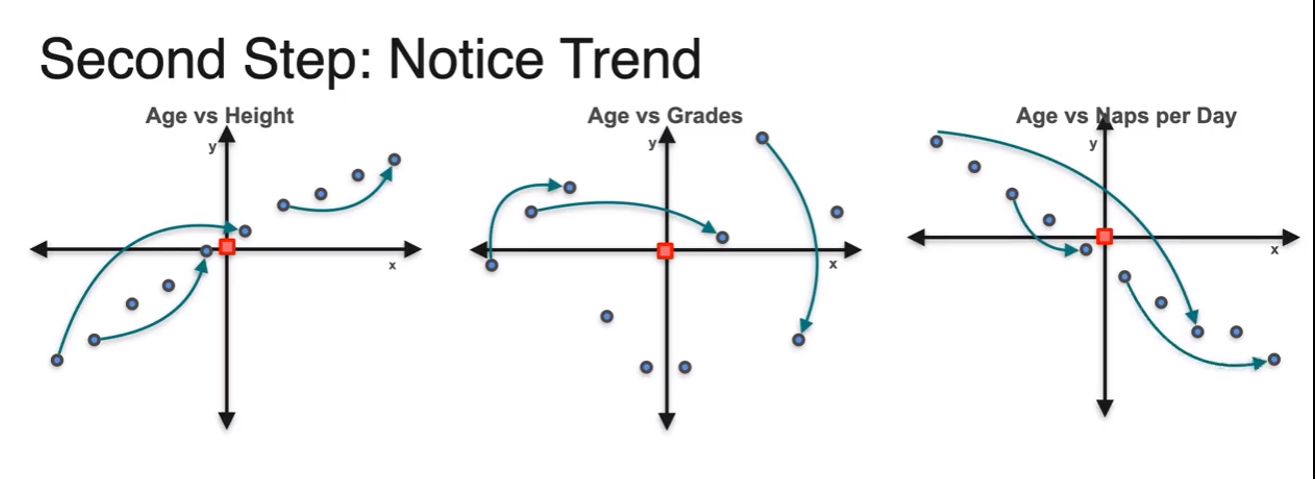
• then how to calculate covariance

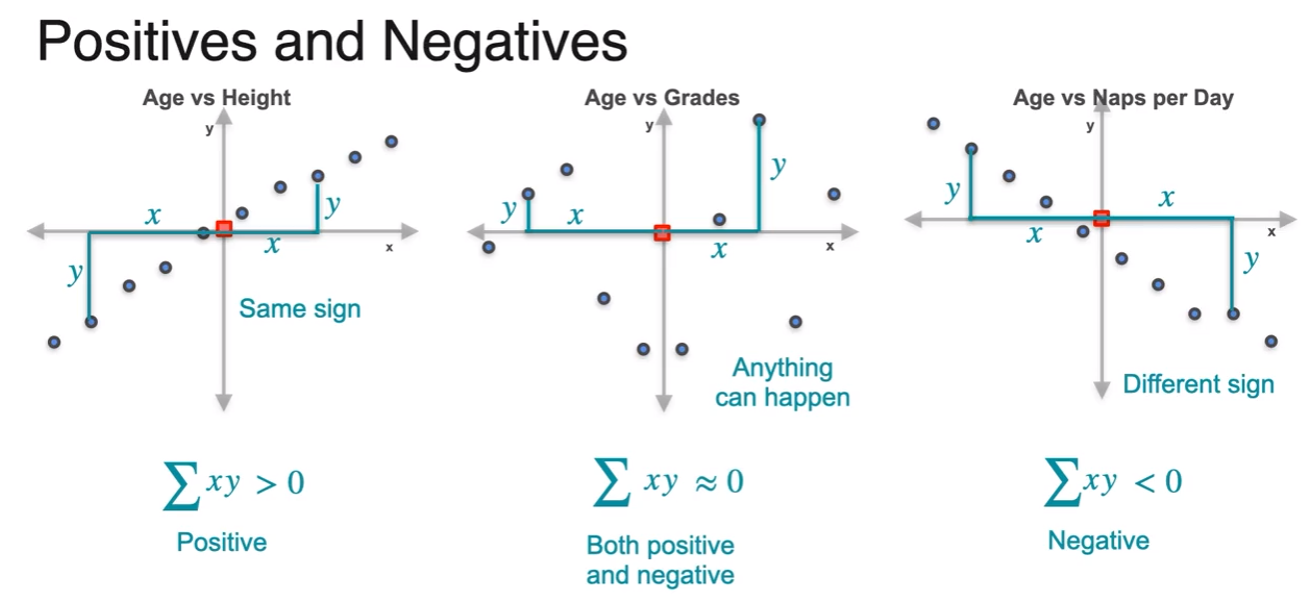
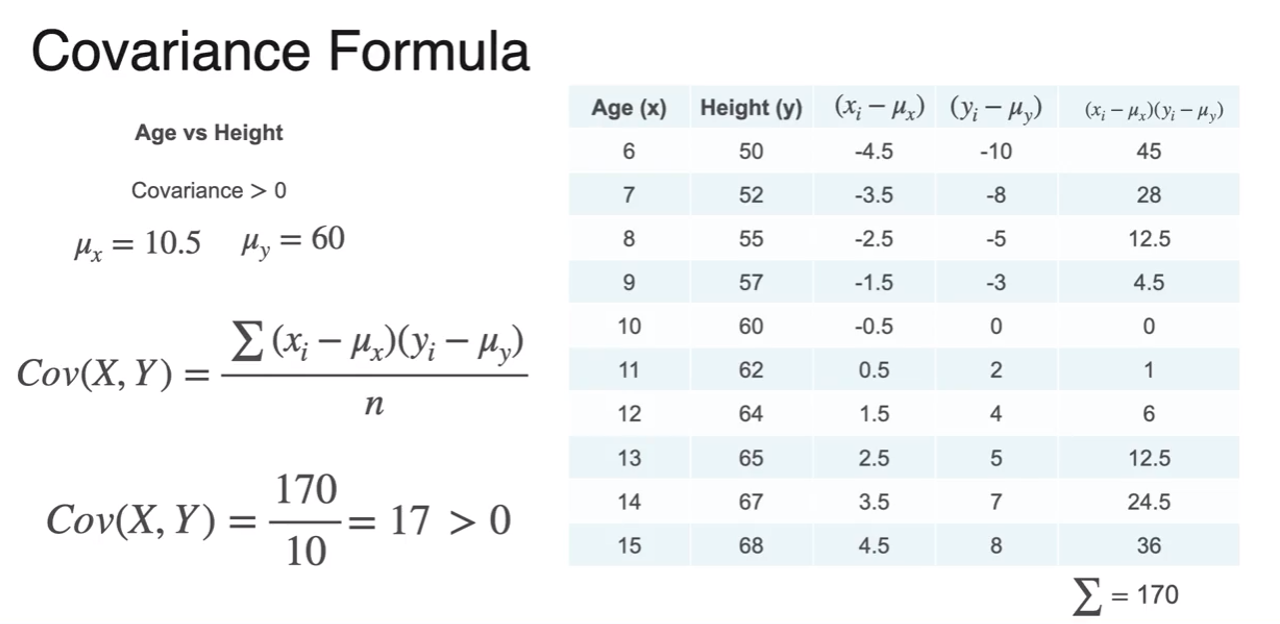
• positively correlated

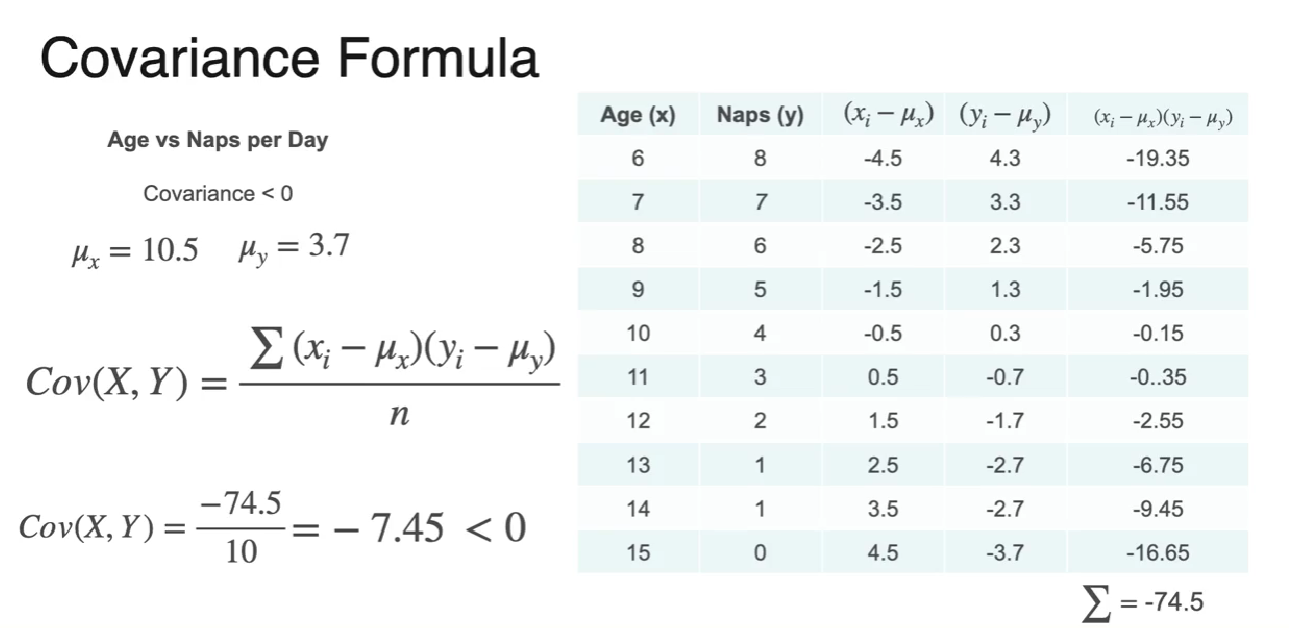
• negatively correlated

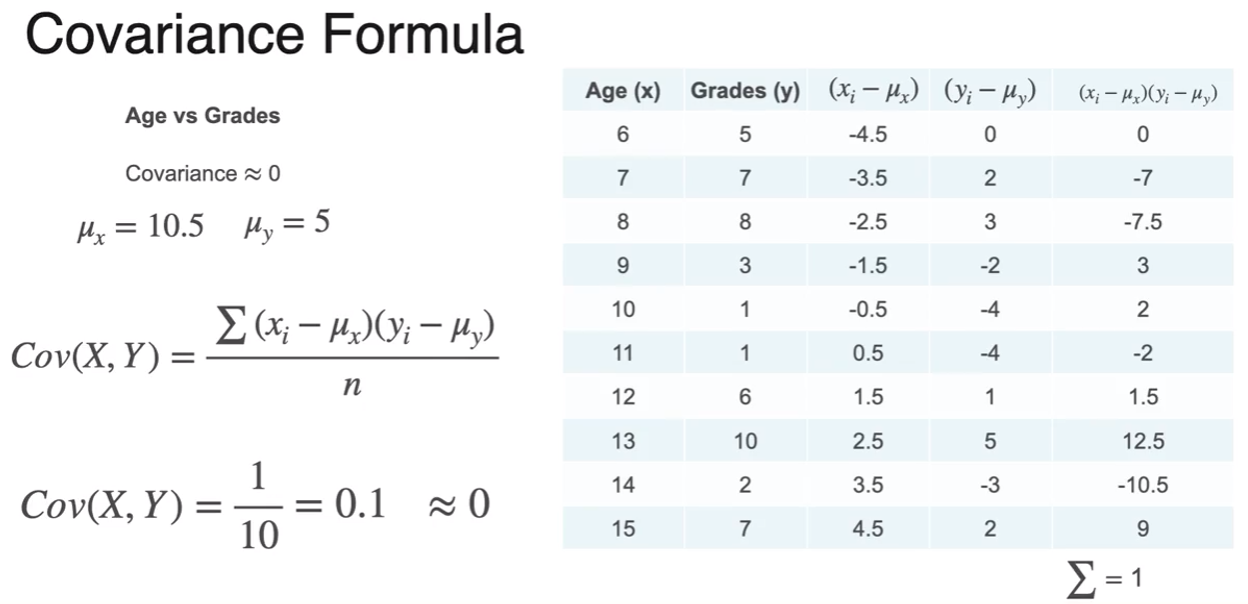
• little influence

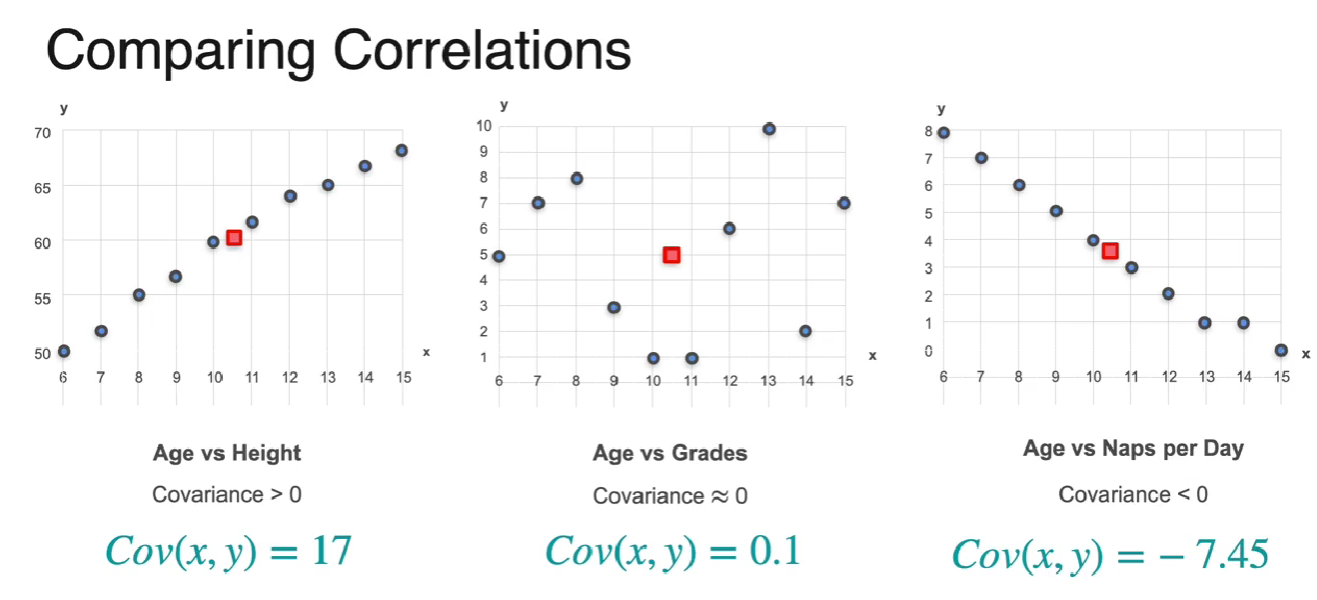
Covariance of a Probability Distribution

• these games are same only consider one player

• game 1 : cov > 0

• game 2 : cov < 0

• game 3 : cov = 0

Covariance Matrix

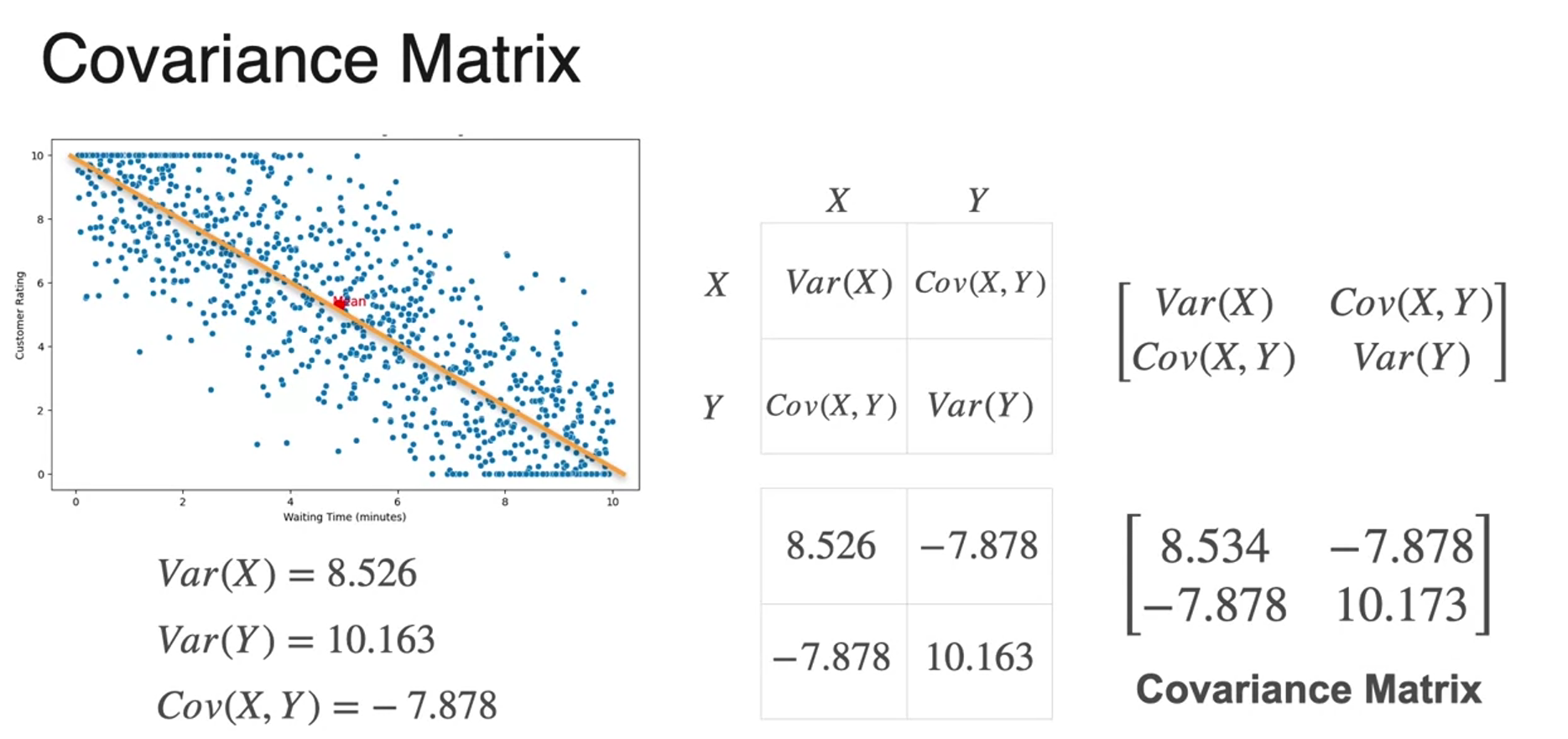
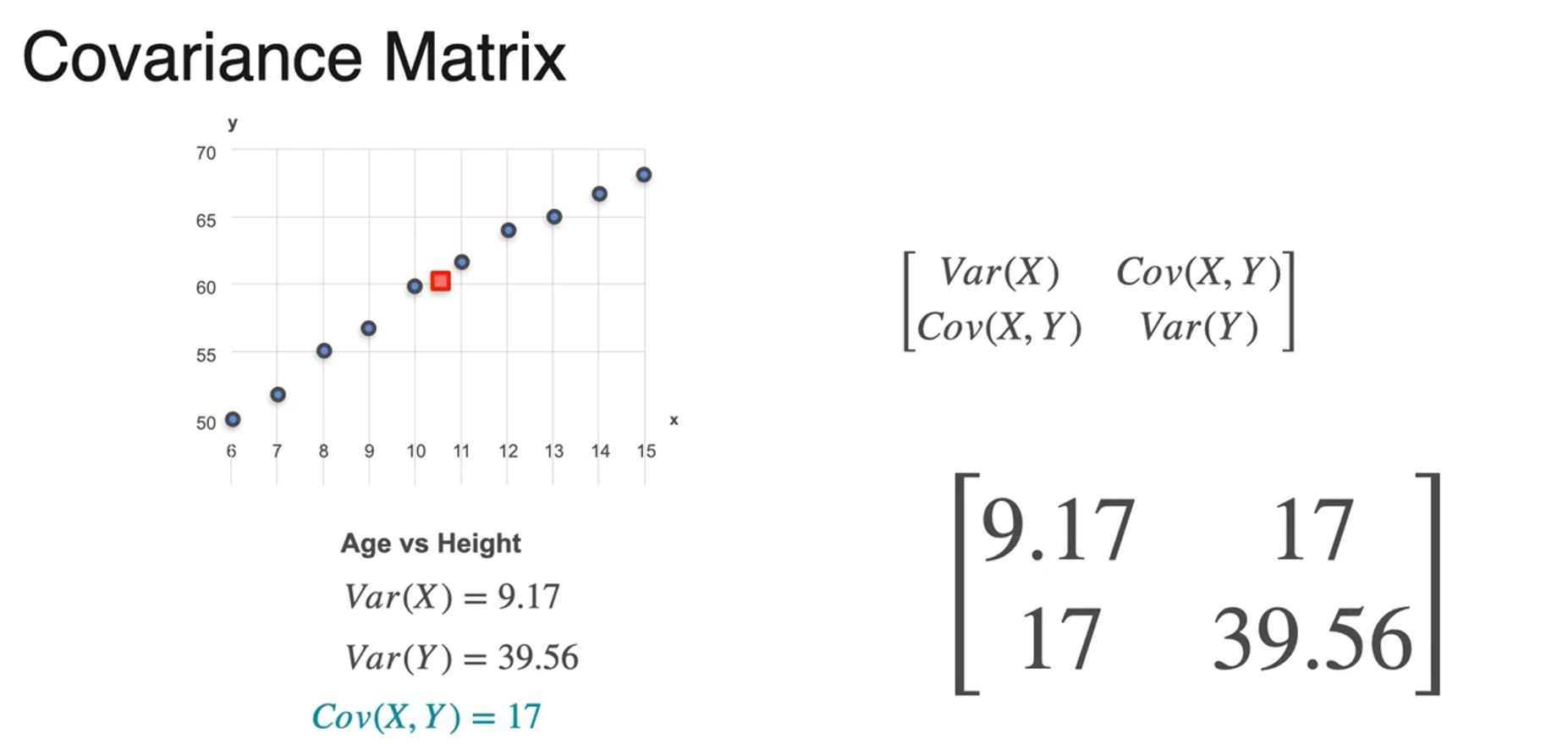
• this matrix is called sigma, the covariance matrix

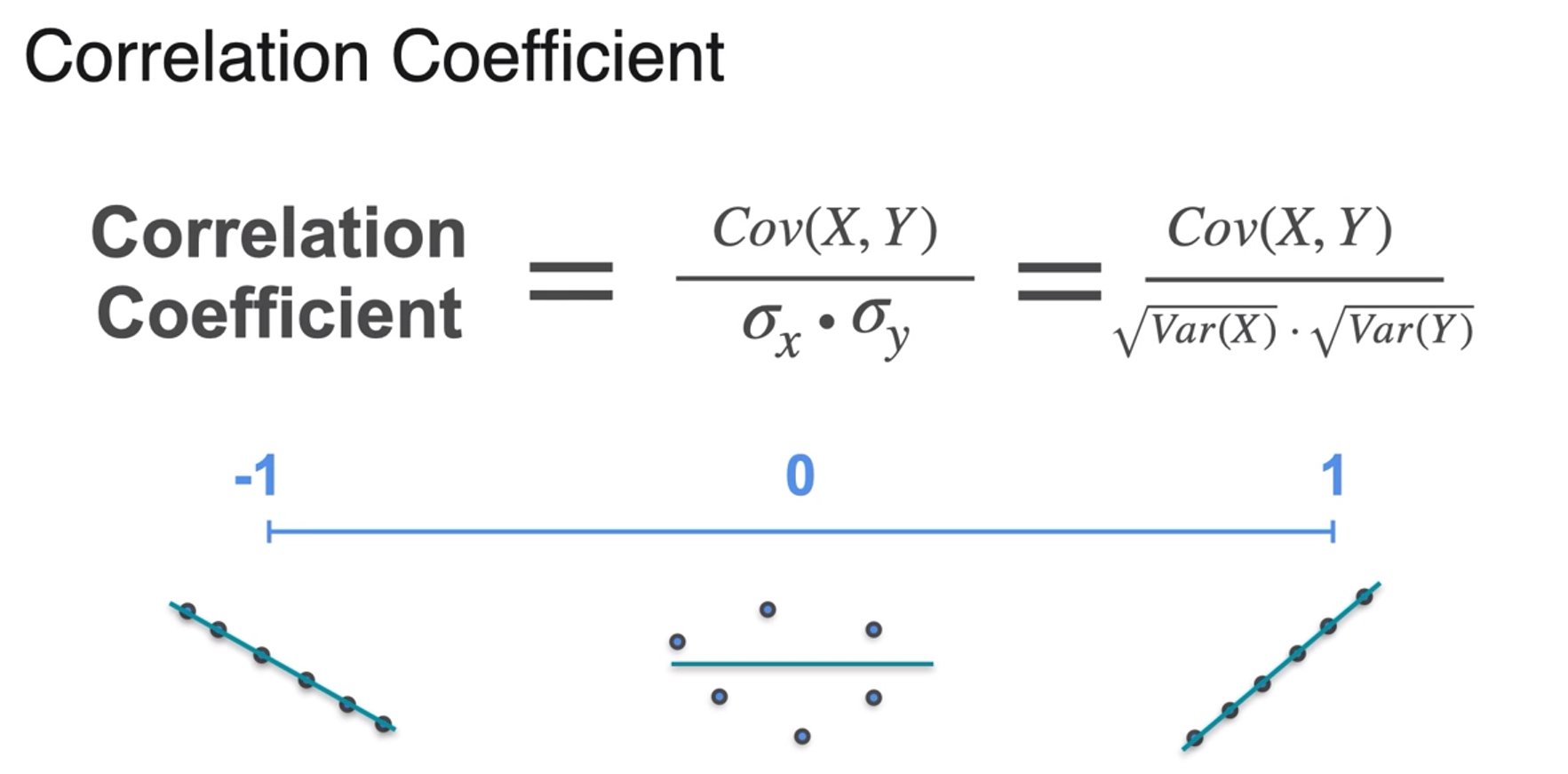
Correlation Coefficient

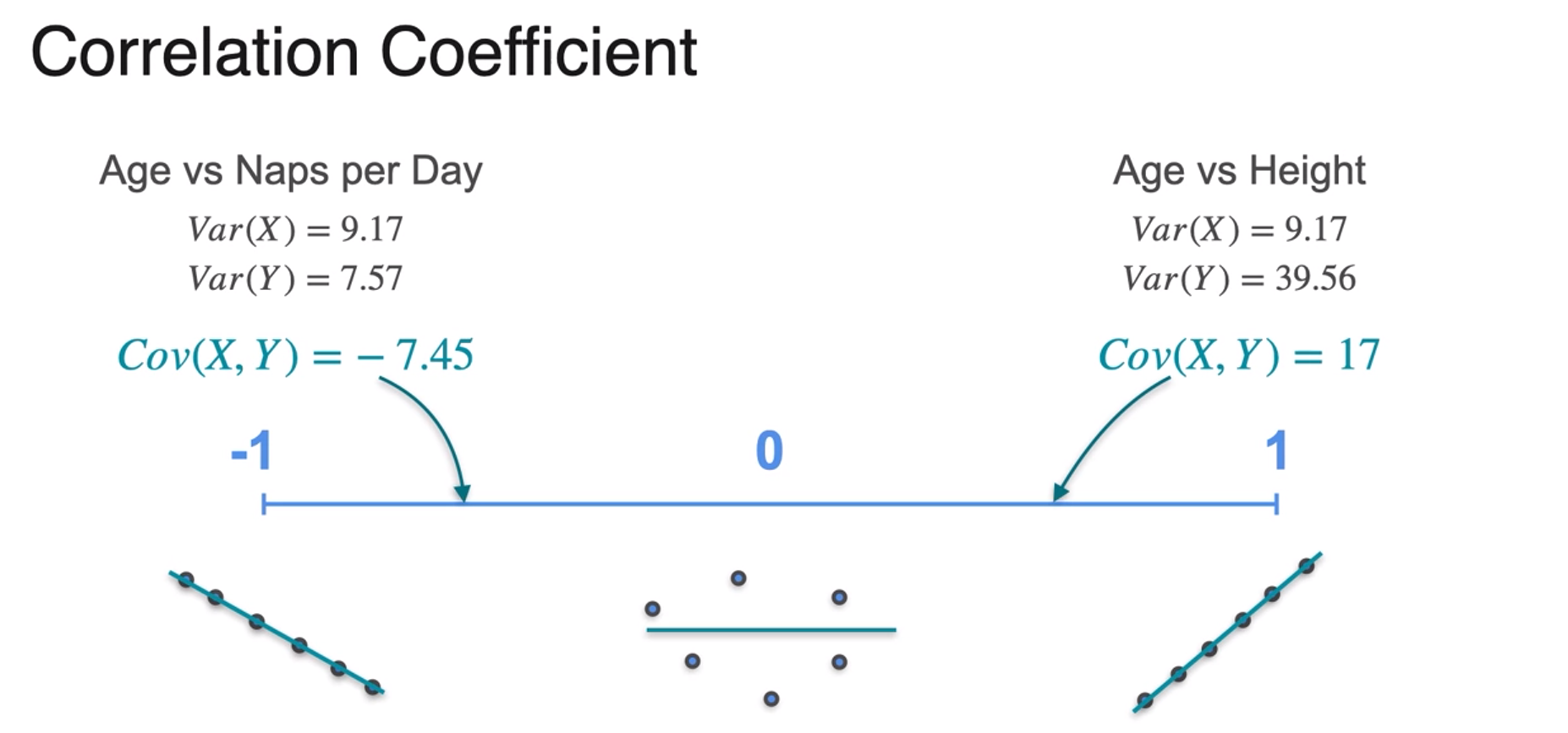
• -7.45 and 17 doesn't actually fit in there but after standardizing they will

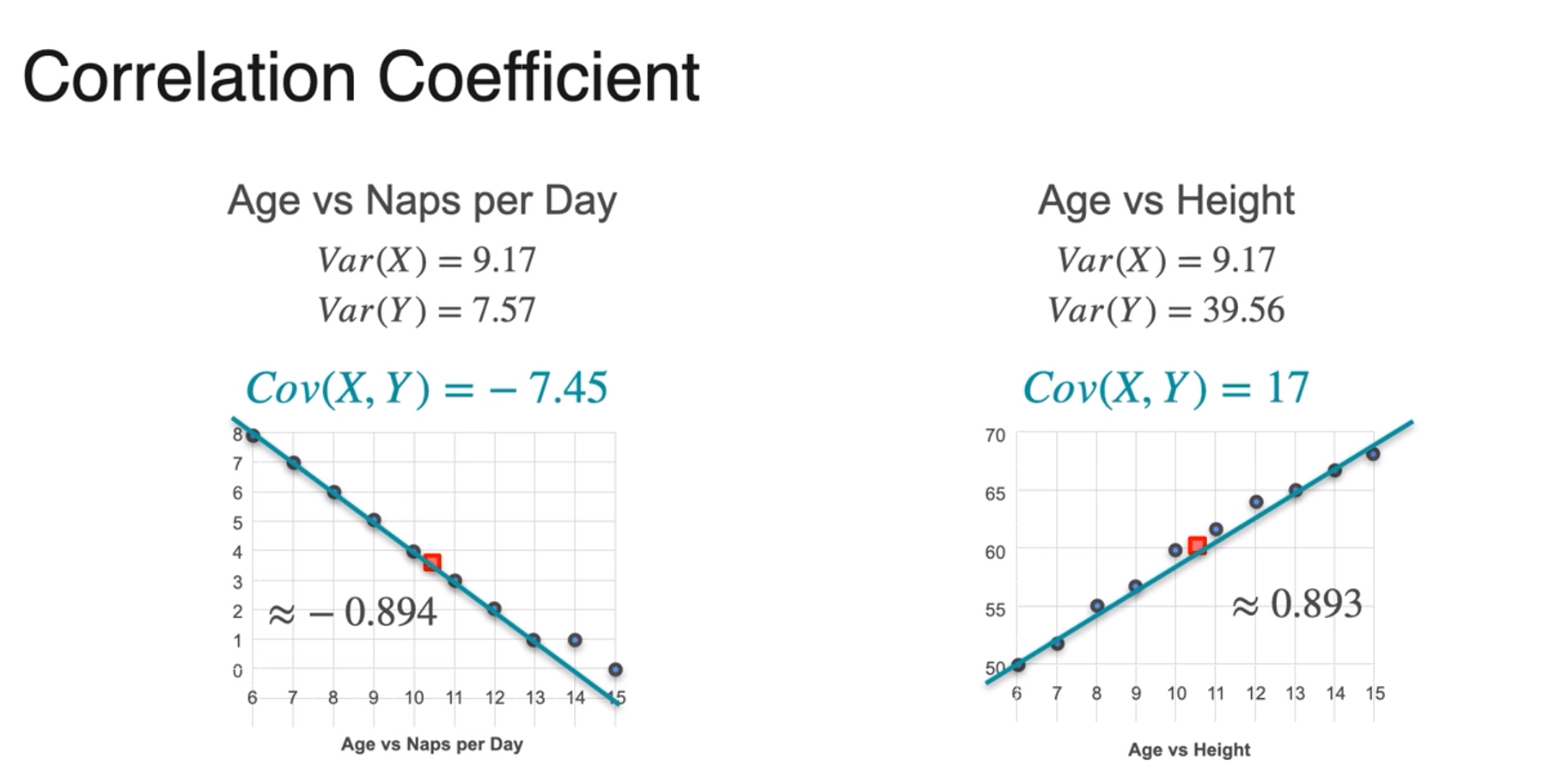
• despite of big difference in magnitude of covariances the magnitude of the correlation coefficient is always small
  • -1 < correlation coefficient < 1
  • only direction of diagonal is different

Multivariate Gaussian Distribution

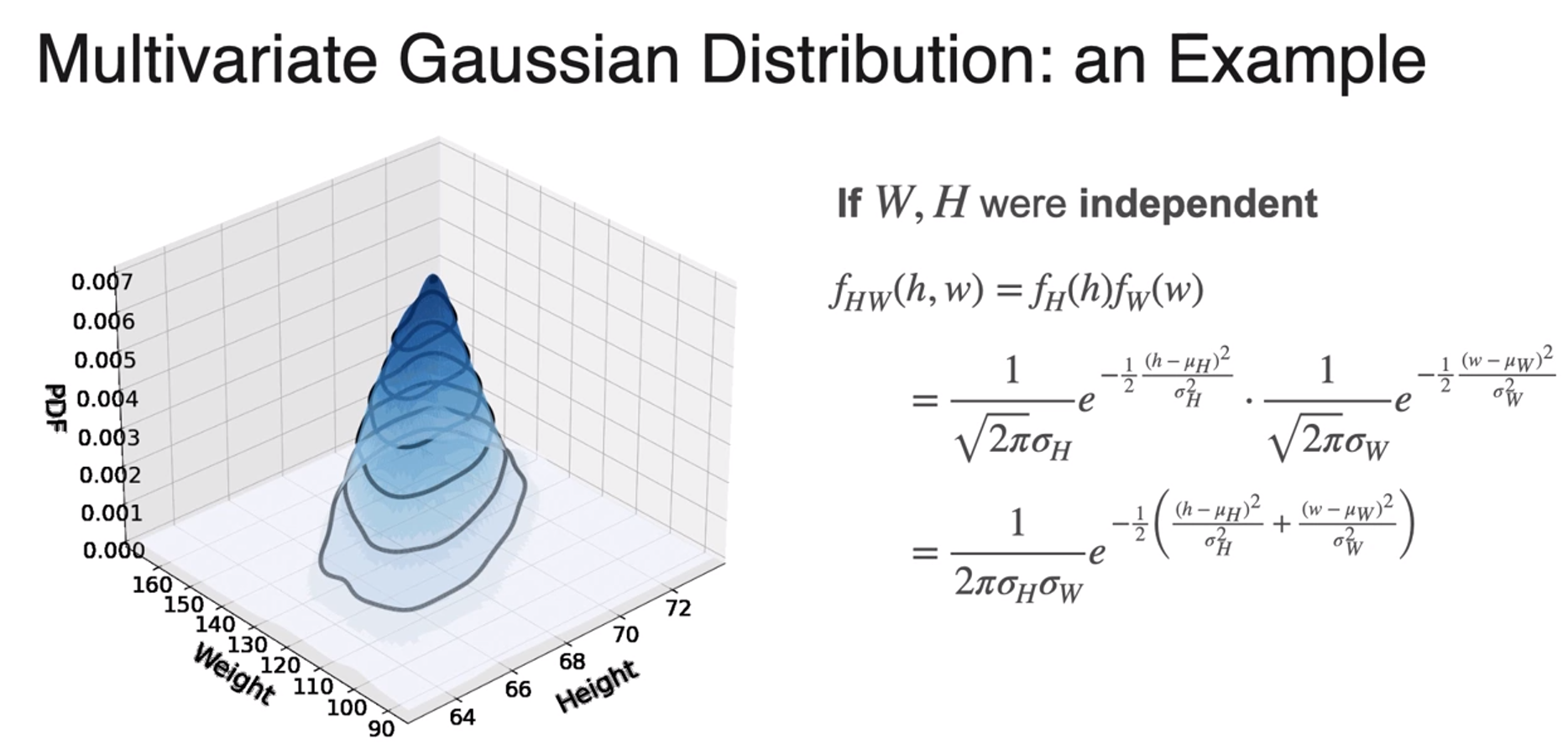
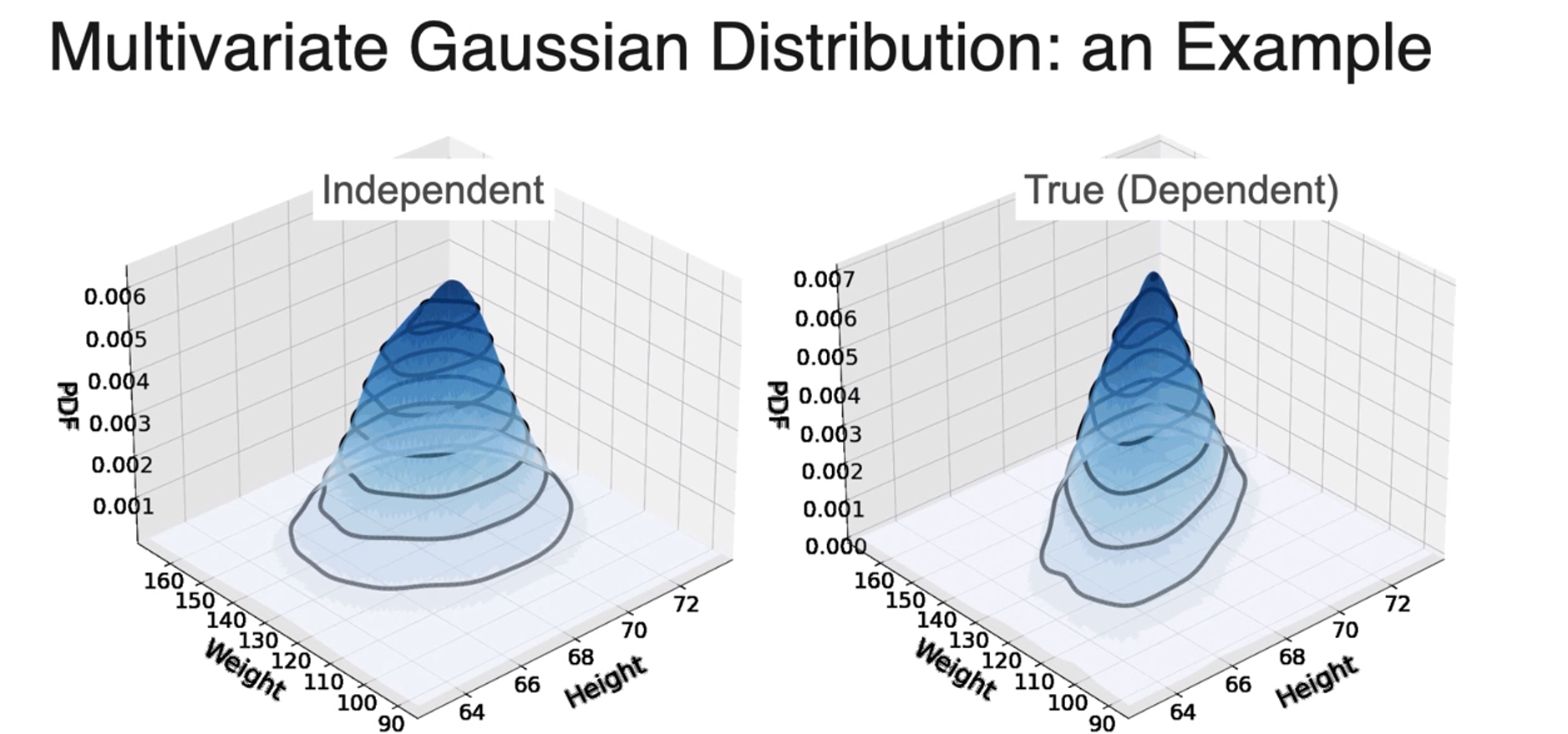
• what causing deformation of joint distribution -> covariance

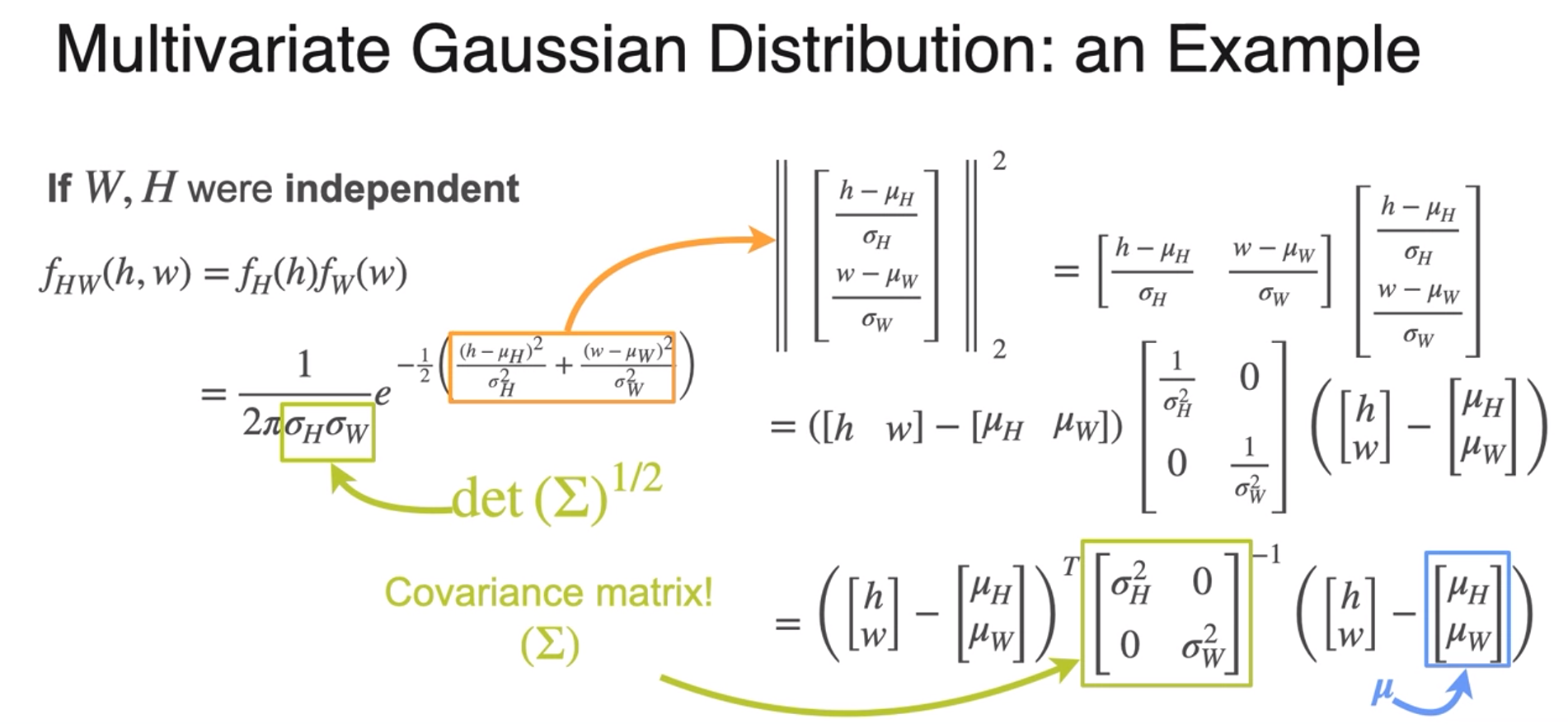
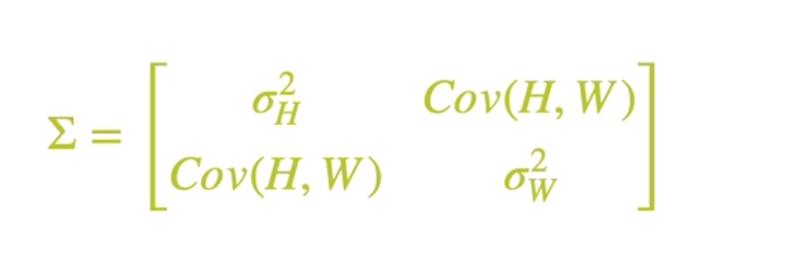
• when dependent