[Python] 알고리즘

sliver gun·2024년 10월 12일
알고리즘파이썬

알고리즘

목록 보기
15/30

🔰목차

  1. 서론
  2. 알고리즘
    • 브루트포스
    • 백트래킹
    • 다이나믹 프로그래밍
    • 누적 합
    • 그리디 알고리즘
    • 이분 탐색
    • 투 포인터
    • LCS
    • DFS, BFS
    • 다익스트라
    • 플로이드 워셜
    • 벨만 포드
  3. 결론
  4. 레퍼런스

서론

지난 자료구조에 이어 여러 알고리즘을 요약해보면서 공부를 해보려고 한다.

이번에는 알고리즘의 대략적인 설명과 판단기준, 예시 코드, 관련 백준 문제로 구성하려 한다.

알고리즘

알고리즘 이란 문제를 해결하는 방법을 정의한 일련의 단계적 절차이다.

브루트포스

브루트포스 알고리즘 은 완전탐색 알고리즘으로 모든 경우의 수를 다 대입해보는 알고리즘을 뜻한다.

전수조사, 무차별 대입, 계산 노가다 라고 불린다.

이후 설명할 백트래킹, DFS, BFS의 경우도 브루트포스에 해당한다.

판단 기준

모든 경우의 수를 판단하는 특성상 시간복잡도가 크므로 문제의 조건이 작다면 브루트포스를 의심해 볼 수 있다.

브루트포스의 경우 그저 순차 탐색을 하는 것이기 때문에 암기할만한 부분은 따로 없다.

# For문을 이용한 순차 탐색
for i in range(1000):
	if '특정 조건' is True:
		print(i)
		break

💡 관련 백준 문제

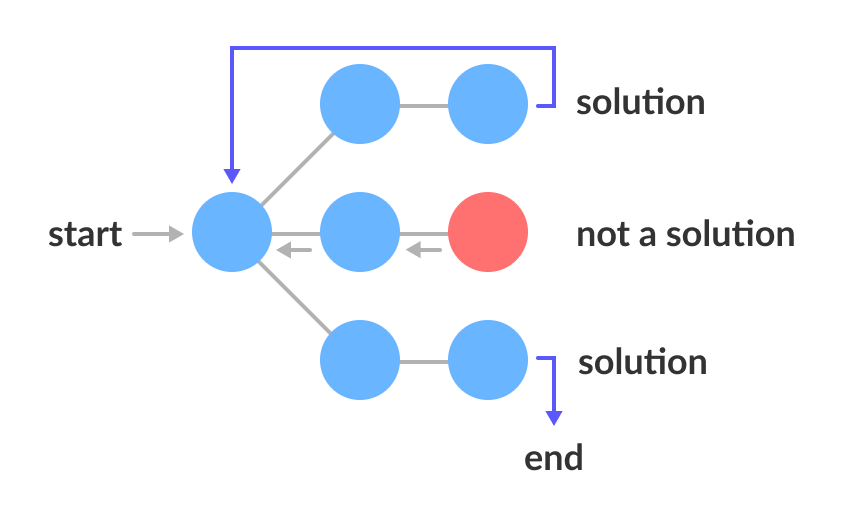
백트래킹

백트래킹 이란 해를 찾는 도중 해가 되지 않을 경우 다시 돌아가 해를 구하는 알고리즘을 말한다.

여러 분기점에서 한 분기점을 조사할 때 해가 될 가능성이 있다면 유망하다(promising)이라고 하며, 유망하지 않다면 가지치기(pruning) 한다.

중간에 가지치기를 하기 때문에 경우의 수가 줄어들어 효율적이다.

판단 기준

대개 재귀 형태로 구현하며 그래프와 같은 비선형 자료를 브루트포스 해야할 때 쓰인다.

백트래킹은 재귀함수를 통해 구현하면서 원소를 선택할 때 한정 조건 을 통해 가지치기(pruning)을 하도록 구현한다.

def BT(depth, m):
	if depth == m:
		# 선택한 원소로 기반으로 결과를 계산하는 부분
	else:
		# 원소를 선택하는 부분

💡 관련 백준 문제

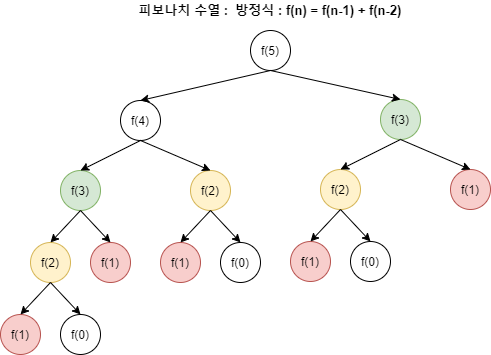
다이나믹 프로그래밍

DP(다이나믹 프로그래밍) 은 복잡한 문제를 작은 하위 문제로 나누어 해결하는 알고리즘입니다.

사실 알고리즘이라기 보단 문제 해결법에 가깝다고 볼 수 있다.

메모이제이션(Memoization)을 사용해 작은 하위 문제의 중복되는 계산 결과를 저장한 뒤 점차 큰 문제의 해를 구하는 것이 특징입니다.

판단 기준

이전 선택이 이후 선택에 영향을 주는 경우 대개 DP(다이나믹 프로그래밍)이다.

대표적으로 피보나치 함수, 배낭문제, LCS가 DP 적용 문제이다.

# 피보나치 함수
def fibonacci(n):
	if n <= 0:
    return -1 if n != 0 else 0
  mem = [0 for _ in range(n+1)]
  mem[1] = 1
  for i in range(2, n+1):
      mem[i] = mem[i-1] + mem[i-2]
  return mem[n]
  
# 배낭 문제
for i in range(1, N+1):
  for w in range(L[1][0], K+1):
    if L[i][0] > w:
	    # 현재 물건을 배낭에 넣을 수 없을 때
      DP[i][w] = DP[i-1][w]
    else:
	    # 현재 물건을 배낭에 넣을 수 있을 때
      DP[i][w] = max(DP[i-1][w-L[i][0]] + L[i][1], DP[i-1][w])

💡 관련 백준 문제

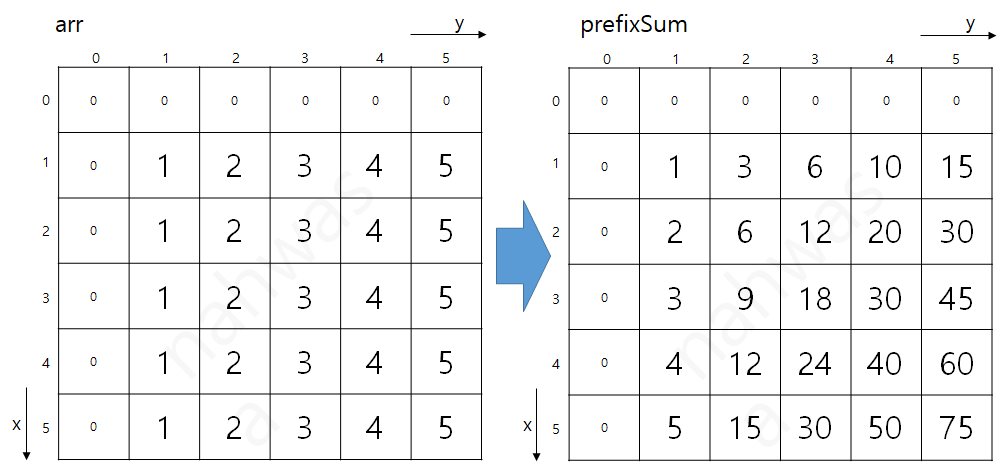
누적 합

누적 합 이란 특정 배열의 어떤 구간의 합을 빠르게 계산할 수 있도록 하는 알고리즘이다.

어떤 변하지 않는 배열이 있을 때 각 원소까지의 합을 미리 계산해두는 것이 특징이다.

S[i] = A[0] + A[1] + ... + A[i] 처럼 누적 합 배열 S를 구해놓으면

A[i]부터 A[j]까지의 합 = S[j] - S[i-1] 이 된다.

판단 기준

특정 구간의 합을 여러 번 접근하는 문제에서 사용된다.

기존에 있는 배열을 for문을 통해 누적합 배열에 차례대로 추가하면 된다.

계산의 편의를 위해 첫 원소를 0으로 초기화하기도 한다.

# 누적 합 구하기
L = list(map(int, input().split()))
sum = [0]
for i in range(len(L)):
    sum.append(sum[i] + L[i] if i > 0 else L[i])

💡 관련 백준 문제

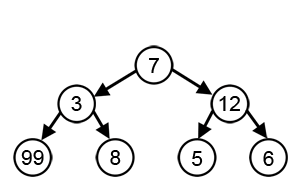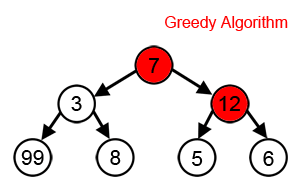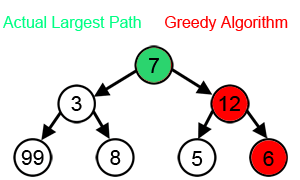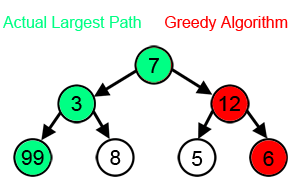
그리디 알고리즘

그리디 알고리즘 은 현재 시점에서 가장 최선이라고 생각되는 선택으로 해결하는 알고리즘이 있다.

그리디 알고리즘의 특징으로는 2가지가 있다.

탐욕적 선택 속성: 각 단계에서 가장 최선이라고 판단되는 선택을 함.

최적 부분 구조: 문제의 최적해가 부분 문제들의 최적해들로 구성되어야 함.

즉, 부분적으로 최선의 선택이 해를 선택하여 전체적으로도 최적의 해를 찾을 수 있는 전략이다.

판단 기준

N이 크면서 알고리즘이 보이지 않는 경우라면 대개 그리디 알고리즘이다.

매 순간마다 최선의 선택을 하도록 코드를 작성하면 된다.

# 동전 문제
def greedy_coin_change(coins, amount):
  coins.sort(reverse=True)  # 동전 내림차순 정렬
  count = 0
  for coin in coins:
    # 현재 동전으로 거슬러 줄 수 있는 개수
    count += amount // coin
    amount %= coin  # 남은 금액
  return count

💡 관련 백준 문제

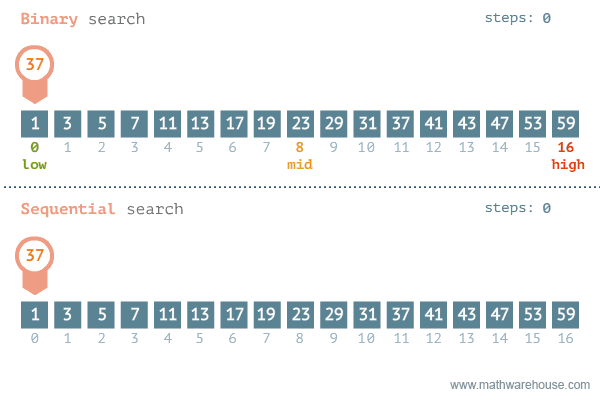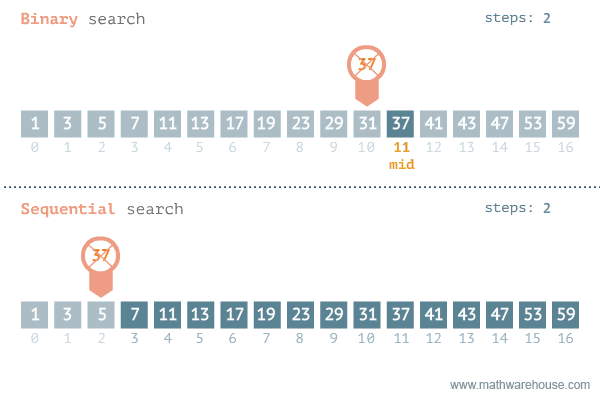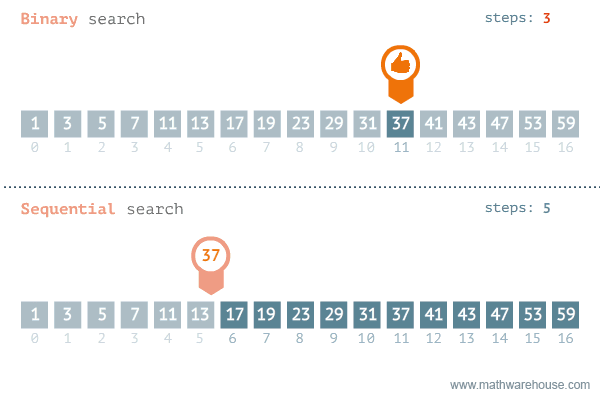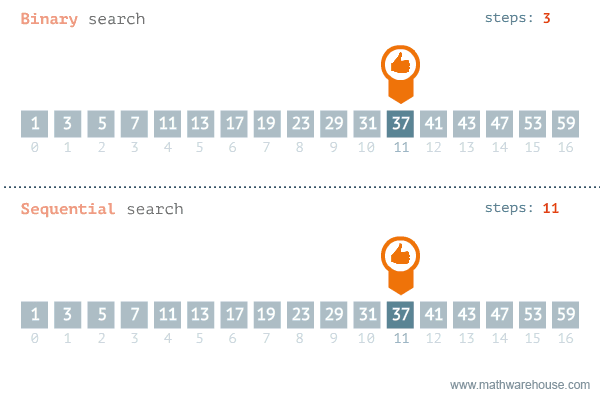
이분 탐색

이분 탐색 은 정렬된 배열에서 특정 값을 찾기 위한 효율적인 탐색 알고리즘이다.

이분 탐색은 결정 문제 에서 답이 이분법 적일 때 사용한다.

결정문제 : 답이 예, 아니오 로 결정되는 문제

판단 기준

O(logN) 내에 특정 값을 찾아야 하기에 N이 10억 정도로 큰 경우가 많다.

파이썬에서는 반복문을 이용하거나 bisect 라이브러리를 사용하여 구현할 수 있다.

# For문을 통한 구현
def binary_search(arr, target, low, high):
	while low <= high:
		mid = (low + high) // 2
		# target을 찾은 경우
		if arr[mid] == target:
			return mid
		# target이 오른쪽에 존재하는 경우
		elif arr[mid] > target:
			high = mid - 1
		# target이 왼쪽에 존재하는 경우
		else: # arr[mid] < target
			low = mid + 1
	return None
	
# bisect 라이브러리를 이용하는 경우
from bisect import bisect_left, bisect_right

arr = [1, 2, 3, 4, 5]
target = 3

# arr에 target을 왼쪽/오른쪽에 삽입할 인덱스를 출력함

print(bisect_left(arr, target))
# 2
print(bisect_right(arr, target))
# 3

💡 관련 백준 문제

투 포인터

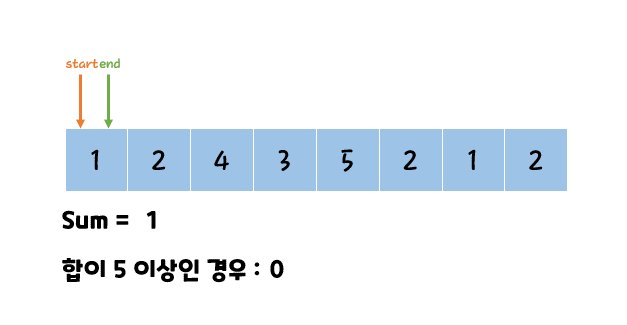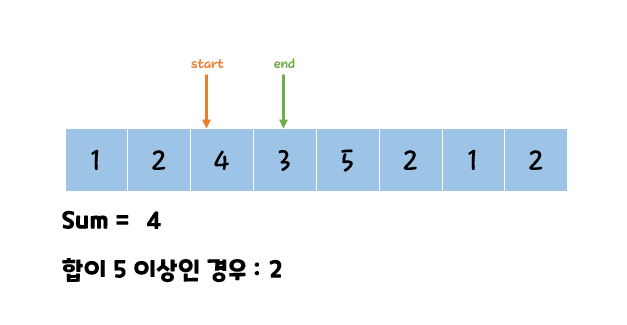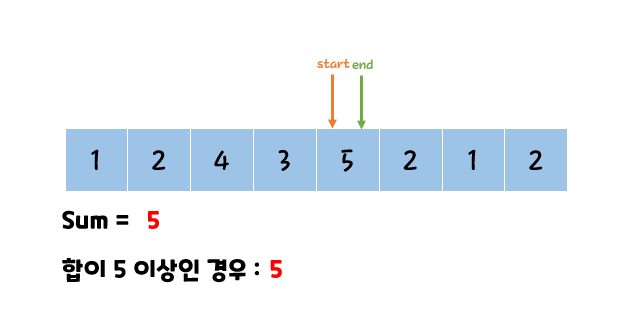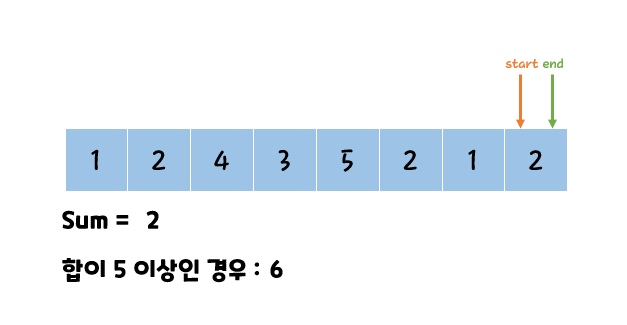
투 포인터 란 특정 구간의 합을 찾거나 정렬된 배열에서 포인트 2개를 옮겨가면서 조건에 맞는 값을 찾을 때까지 탐색하는 알고리즘이다.

O(N^2)가 걸리는 문제를 O(N)에 해결 가능하다.

판단 기준

두 인덱스를 탐색하고 O(N^2)로 시간 초과가 발생한다면 투 포인터 알고리즘일 확률이 높다.

# 특정 구간의 합을 찾는 문제
def count_subarrays_with_sum(arr, target_sum):
    start, end = 0, 0
    current_sum = 0
    count = 0

    while end < len(arr):
        # `current_sum`에 `arr[end]`를 더해서 현재 구간의 합을 업데이트
        current_sum += arr[end]

        # `current_sum`이 `target_sum`보다 크면 `start`를 증가시켜 구간을 줄임
        while current_sum > target_sum and start <= end:
            current_sum -= arr[start]
            start += 1

        # `current_sum`이 `target_sum`과 같으면 카운트 증가
        if current_sum == target_sum:
            count += 1

        # `end`를 오른쪽으로 이동
        end += 1

    return count

# 정렬된 배열에서 두 수의 합을 찾는 문제
while True:
	# 기저조건
  if start == end:
    break
  num = L[start] + L[end]
  if num >= X:
	  # 부분 합이 target과 같다면 카운트
    if num == X:
      cnt += 1
		# 부분 합이 target보다 크다면 end-1
    end -= 1
  else:
	  # 부분 합이 target보다 작다면 start+1
    start += 1

💡 관련 백준 문제

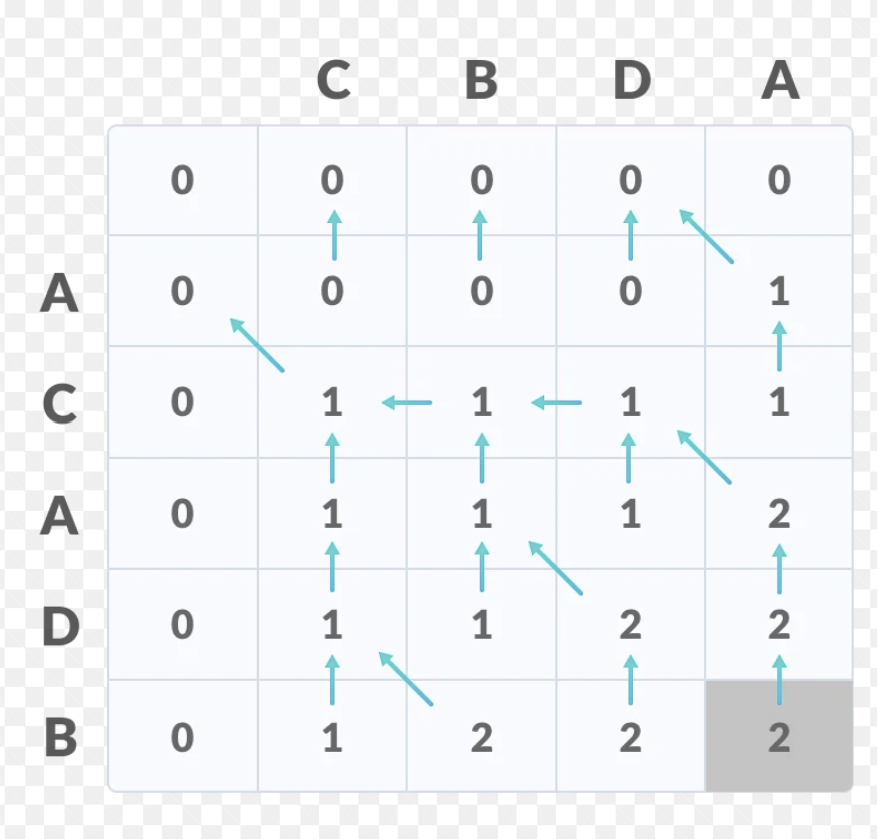
LCS

링크텍스트

LCS (Longest Common Subsequence, 최장 공통 부분 수열) 은 두 개의 문자열에서 순서를 유지하며 공통으로 나타나는 최장 부분 수열을 찾는 문제이다.

LCS를 찾는 방법은 2차원 DP 테이블을 사용하는 방법이 있다.

판단 기준

최장 공통 부분 수열/문자열 이라는 핵심 키워드가 존재하므로 키워드 존재 유무에 따라 판단 가능

기본적으로

  • 문자가 같으면 : dp[i][j] = dp[i-1][j-1] + 1
  • 문자가 다르면 : dp[i][j] = max(dp[i-1][j], dp[i][j-1])
# LCS
def lcs(X, Y):
  # 두 문자열의 길이
  m = len(X); n = len(Y)

  # DP 테이블 초기화 (모두 0으로 채움)
  dp = [[0 for i in range(n + 1)] for j in range(m + 1)]

  # DP 테이블 채우기
  for i in range(1, m + 1):
    for j in range(1, n + 1):
      # 문자가 같으면
      if X[i - 1] == Y[j - 1]:  
        dp[i][j] = dp[i - 1][j - 1] + 1
      # 문자가 다르면
      else:  
        dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

  return dp[m][n]

💡 관련 백준 문제

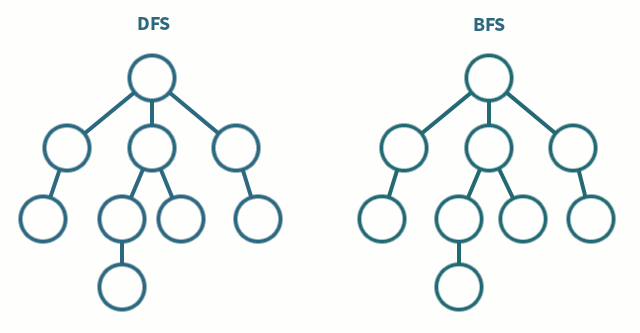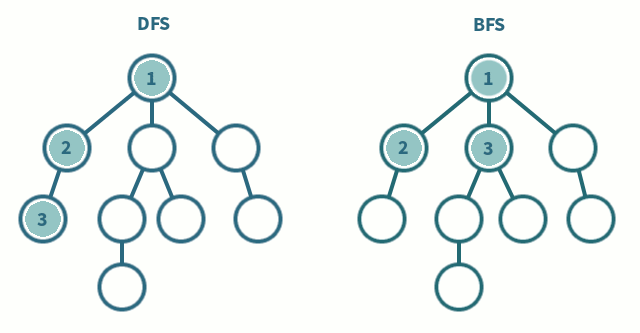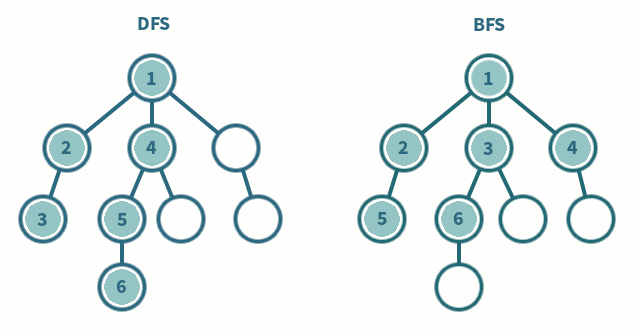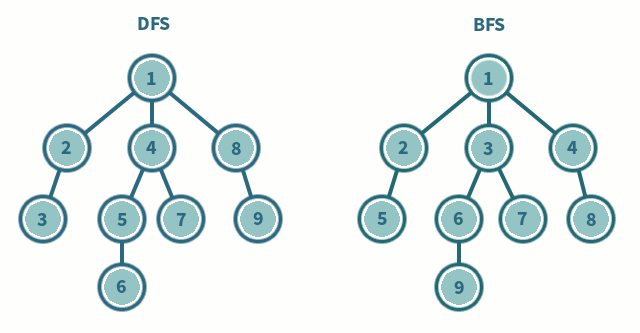
DFS, BFS

DFS (Depth-First Search, 깊이 우선 탐색) 와 BFS (Breadth-First Search, 너비 우선 탐색) 는 그래프나 트리 구조를 탐색하는 방법이다.

DFS는 한 노드에서부터 가능한 깊이까지 탐색하고 돌아오는 방식으로 백트래킹과 유사하다.

BFS는 한 노드에서 자신과 인접한 노드를 먼저 탐색 후 그 다음 노드의 인접한 노드를 탐색하는 방식이다.

판단 기준

시간복잡도가 작은 경우

  • DFS의 경우 백트래킹 문제로 자주 나온다.
  • BFS의 경우 최단 거리를 찾을 때 간선의 가중치가 동일한 경우 사용한다.
    • 노드 순회 문제, 최단 경로 문제, 연결 요소 문제, 땅따먹기 문제

DFS는 스택이나 재귀를 통해 구현 가능하다.

BFS는 큐를 사용해 구현 가능하다.

# DFS
def dfs(graph, node, visited):
  visited[node] = True
  print(node, end='')

  for i in graph[node]:
    if not visited[i]:
      dfs(graph, i, visited)

# BFS
def bfs(start_node, graph):
  queue = deque([start_node])
  visited = set([start_node])

  while queue:
    curr_node = queue.popleft()

    for next_node in graph[curr_node]:
      if next_node not in visited:
        visited.add(next_node)
        queue.append(next_node)
  return -1

💡 관련 백준 문제

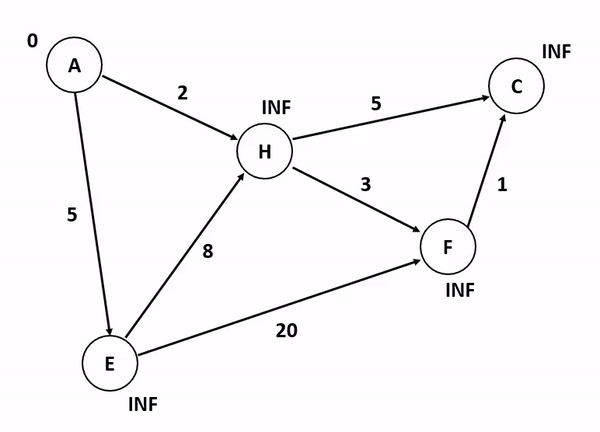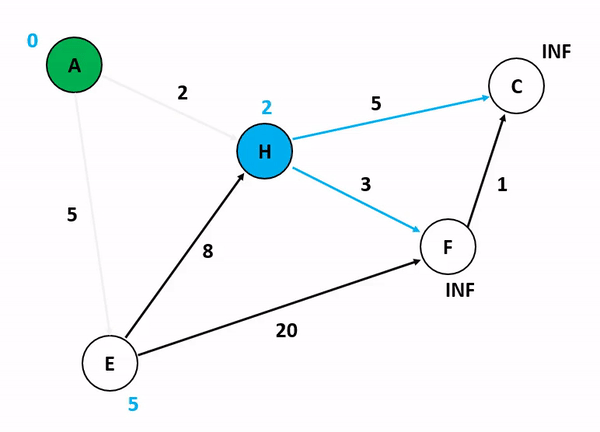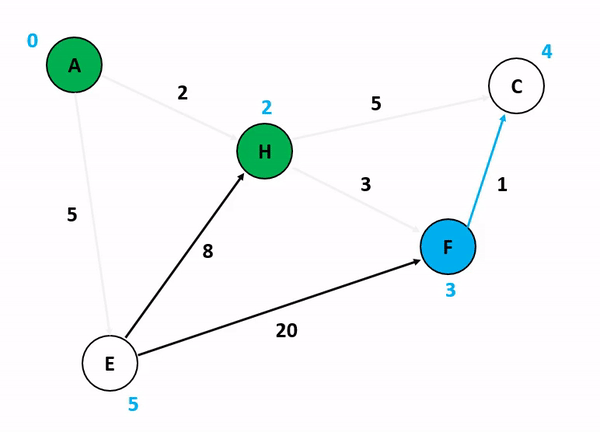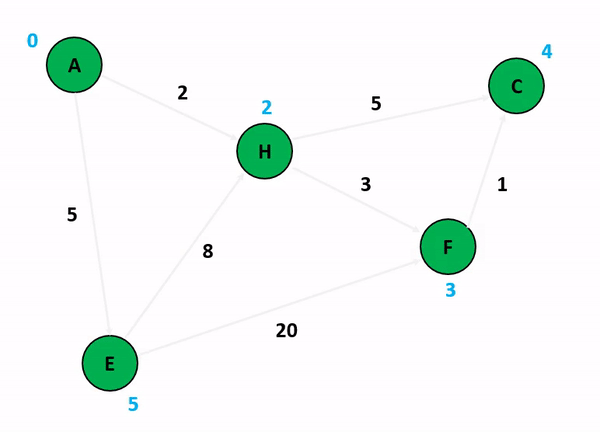
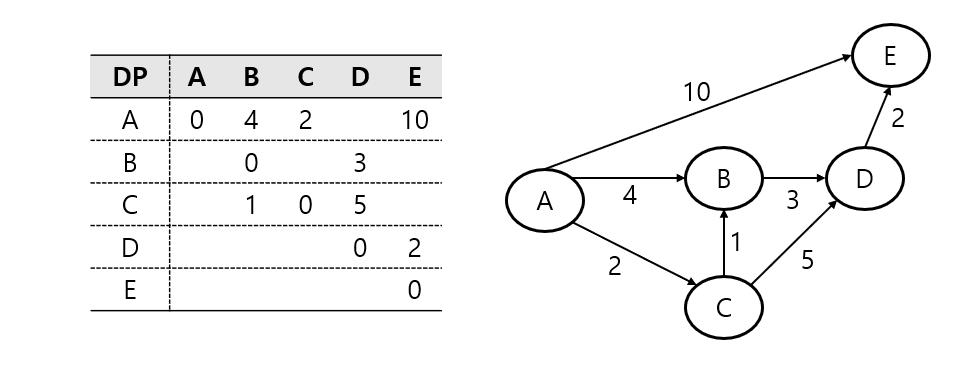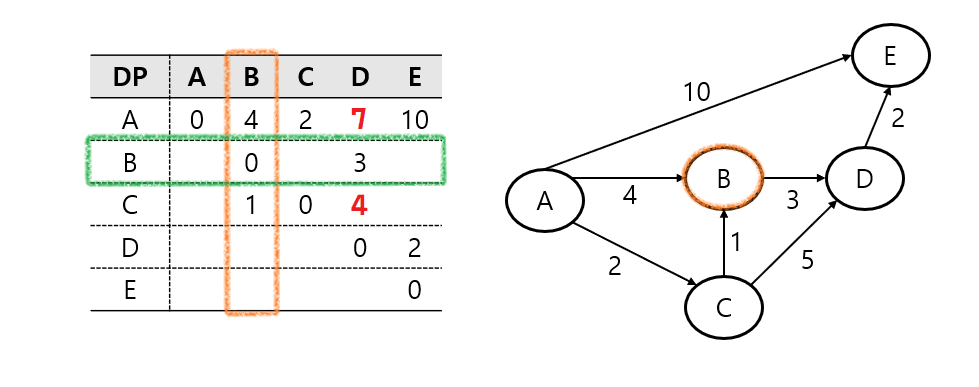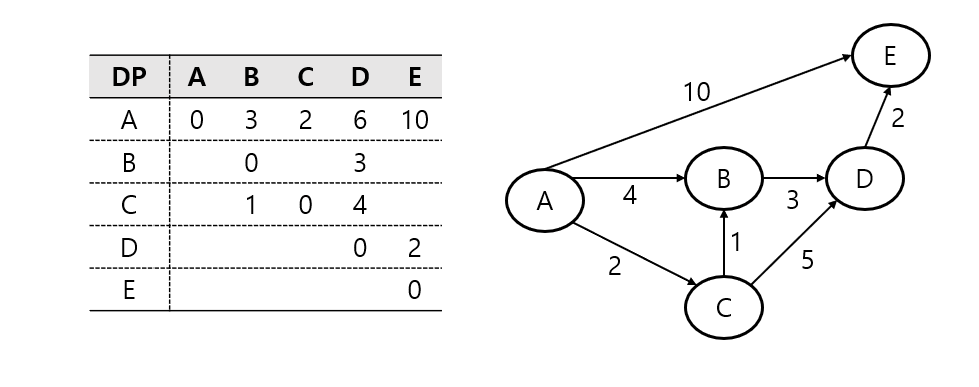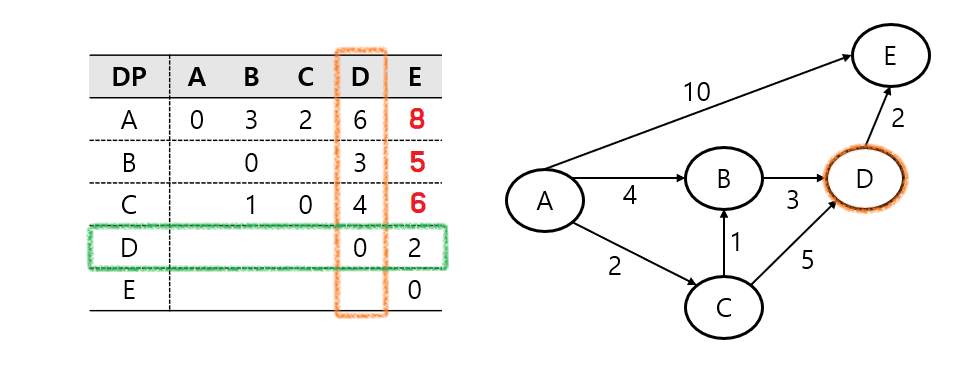
다익스트라

다익스트라 알고리즘(Dijkstra's Algorithm) 가중치가 있는 그래프에서 특정 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘이다.

음의 가중치가 없는 그래프에서만 작동한다.

그리디 알고리즘을 사용해 최단 거리를 선택하며 진행하며 우선순위 큐를 사용해 구현하면 효율적이다.

판단 기준

주로 최소 비용을 찾는 문제에서 쓰이며, 시간복잡도가 O(ElogV)이기에 정점 혹은 간선이 10만개로 큰 경우 다익스트라 문제이다.

최단 거리 테이블에서 최단 거리 노드를 탐색하는 과정을 for문 혹은 우선순위 큐를 이용해 구현 가능하다.

graph는 인접 리스트(딕셔너리)로 되어있다.

# 우선순위 큐
import heapq

def dijkstra(graph, start):
  # 최단 거리를 저장할 딕셔너리
  distances = {node: float('inf') for node in graph}
  distances[start] = 0
  
  # 우선순위 큐 (최소 힙) 초기화
  priority_queue = [(0, start)]
  
  while priority_queue:
    current_distance, current_node = heapq.heappop(priority_queue)
    
    # 이미 처리된 노드라면 무시
    if current_distance > distances[current_node]:
      continue
    
    # 현재 노드와 연결된 다른 인접 노드들을 확인
    for neighbor, weight in graph[current_node]:
      distance = current_distance + weight
      
      # 계산된 거리가 기존 거리보다 짧으면 갱신
      if distance < distances[neighbor]:
        distances[neighbor] = distance
        heapq.heappush(priority_queue, (distance, neighbor))
  
  return distances

💡 관련 백준 문제

플로이드 워셜

플로이드-워셜 알고리즘(Floyd-Warshall Algorithm) 은 모든 노드 간 최단 경로를 구하는 알고리즘이다.

음의 가중치를 가진 간선이 있어도 작동하며 동적 계획법(DP)를 기반으로 합니다.

판단 기준

시간 복잡도가 O(N^3)이나 되기 때문에 N이 매우 작은 경우에만 사용이 가능하다.

임의의 경로에서 다른 경로로 매우 많이 탐색하는 경우 사용된다.

각 노드를 중간 노드로 고려해 모든 쌍의 최단 거리를 업데이트 하면 된다.

삼중 for문을 사용하기에 시간복잡도는 O(N^3)이 된다.

graph는 인접 행렬로 되어있다.

def floyd_warshall(graph):
  # 그래프의 노드 수
  n = len(graph)
  
  # 거리 배열 초기화
  dist = [[graph[i][j] for j in range(n)] for i in range(n)]
  
  # 각 노드를 중간 노드로 고려
  for k in range(n):
    for i in range(n):
      for j in range(n):
        # 최단 거리 갱신
        dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])

  return dist

💡 관련 백준 문제

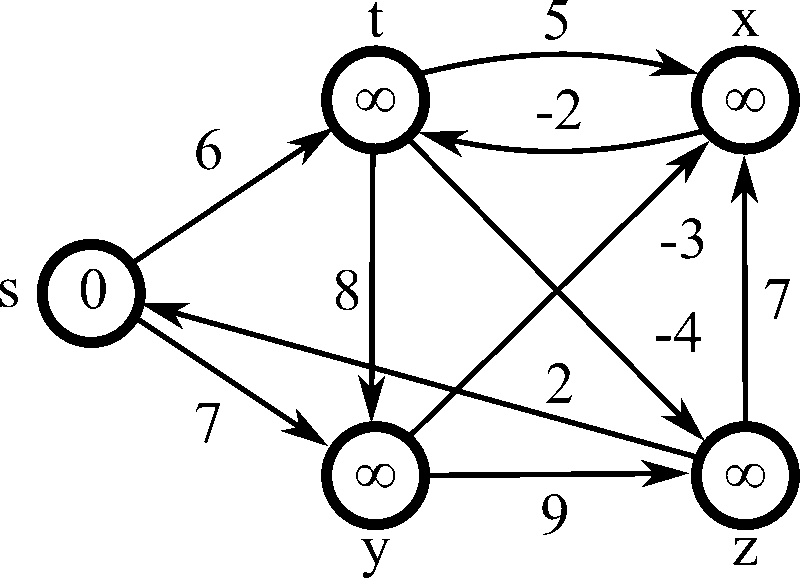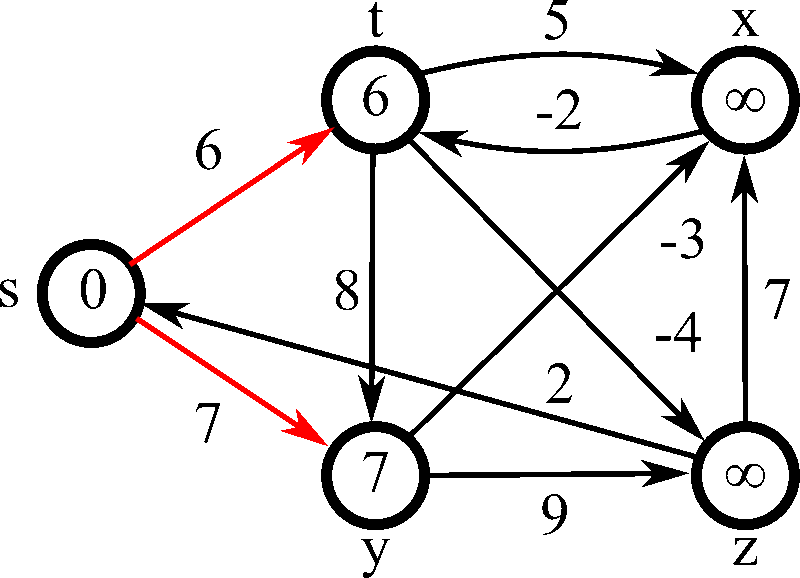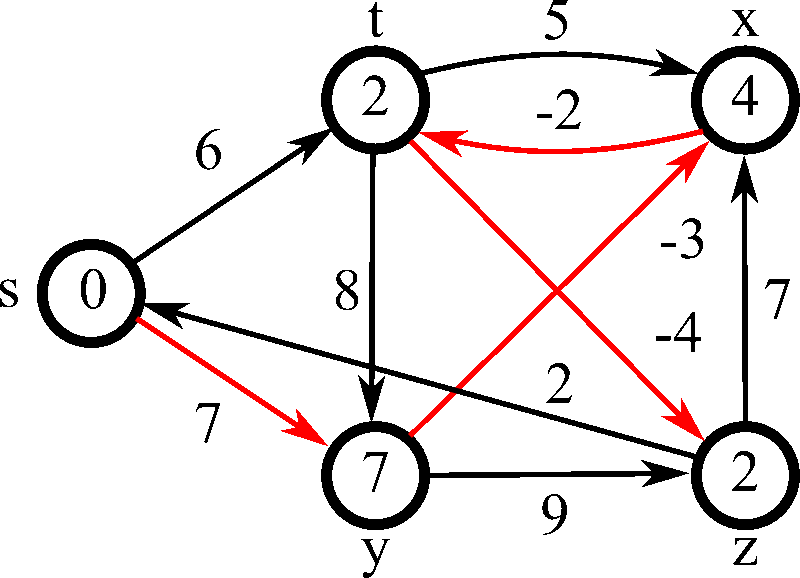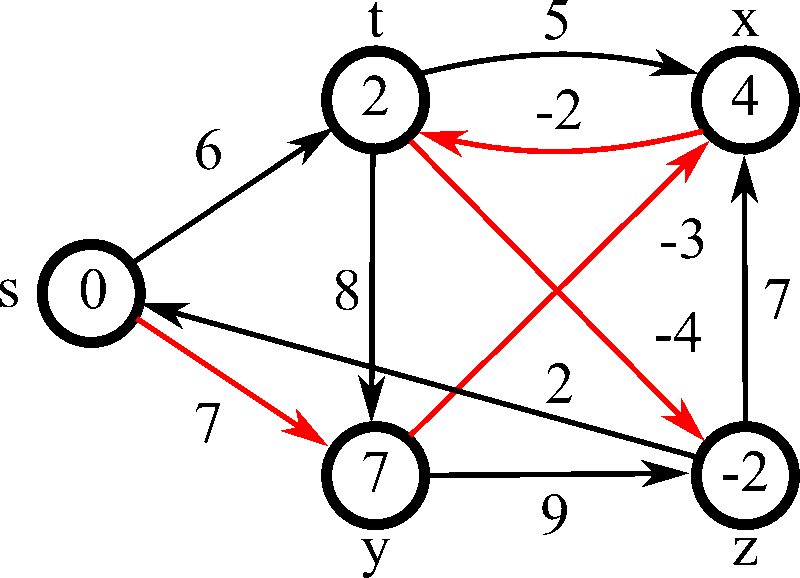
벨만 포드

벨만-포드 알고리즘(Bellman-Ford Algorithm) 은 가중치가 있는 그래프에서 특정 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘이다.

음의 가중치가 있는 그래프에서도 작동하고 음의 가중치 사이클도 탐지 가능하다.

판단 기준

음의 가중치 사이클을 탐지 가능하기에 ‘최단 거리가 무한히 작아질 수 있다’, ‘그런 경우 -1을 출력하라’와 같은 멘트가 있다면 벨만 포드를 사용하면 된다.

코드 출처

import sys
input = sys.stdin.readline
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정

# 노드의 개수, 간선의 개수를 입력받기
n, m = map(int, input().split())
# 모든 간선에 대한 정보를 담는 리스트 만들기
edges = []
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n + 1)

# 모든 간선 정보를 입력받기
for _ in range(m):
    a, b, c = map(int, input().split())
    # a번 노드에서 b번 노드로 가는 비용이 c라는 의미
    edges.append((a, b, c))

def bf(start):
    # 시작 노드에 대해서 초기화
    distance[start] = 0
    # 전체 n - 1번의 라운드(round)를 반복
    for i in range(n):
        # 매 반복마다 "모든 간선"을 확인하며
        for j in range(m):
            cur_node = edges[j][0]
            next_node = edges[j][1]
            edge_cost = edges[j][2]
            # 현재 간선을 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
            if distance[cur_node] != INF and distance[next_node] > distance[cur_node] + edge_cost:
                distance[next_node] = distance[cur_node] + edge_cost
                # n번째 라운드에서도 값이 갱신된다면 음수 순환이 존재
                if i == n - 1:
                    return True
    return False

# 벨만 포드 알고리즘을 수행
negative_cycle = bf(1) # 1번 노드가 시작 노드

if negative_cycle:
    print("-1")
else:
    # 1번 노드를 제외한 다른 모든 노드로 가기 위한 최단 거리를 출력
    for i in range(2, n + 1):
        # 도달할 수 없는 경우, -1을 출력
        if distance[i] == INF:
            print("-1")
        # 도달할 수 있는 경우 거리를 출력
        else:
            print(distance[i])

💡 관련 백준 문제

결론

알고리즘을 하나하나 깊게 파진 않았지만 대략적으로 코드와 작동 원리, 판단 기준을 스스로 정리해놓고 보니까 알고리즘 공부의 큰 그림을 먼저 그려놓은 느낌이 든다.
이제 각 알고리즘 (특히 그래프 관련) 공부를 깊게 하면서 문제들을 풀고 공부해봐야 할 것 같다.

레퍼런스

https://blog.naver.com/mugamta/223375196128

https://codingnotes.tistory.com/231

https://velog.io/@sihoon_cho/Python코딩테스트-코딩테스트-완전정복-BFS-너비우선탐색

profile
sliver gun
이전 포스트

[BOJ 9251] LCS

다음 포스트

[Python] 알고리즘 - 백트래킹

0개의 댓글