[Python] 알고리즘 - 백트래킹

sliver gun·2025년 2월 15일

백트래킹 알고리즘

알고리즘

목록 보기

16/30

백트래킹이란?

뒤로 돌아간다는 뜻이다.

그러니까 해를 찾는 도중에 해가 아니라면 뒤로 돌아가서 다시 해를 찾아가는 기법을 뜻한다.

백트래킹은 완전 탐색(브루투포스) 기법 중 하나이다.

우선 가능한 모든 선택을 트리 구조로 나타낸 후 (일반적으로) 재귀 호출을 통해 탐색한다.

백트래킹에는 핵심적인 개념이 있다.

바로 유망함(Promising)과 가지치기(Pruning)이다.

가지치기(Pruning)

먼저 유망함(Promising)은 진행중인 경로가 해답을 찾을 가능성이 있음을 뜻한다.

그리고 유망함의 반대가 유망하지 않음(nopromising)인데, 바로 이러한 하위 트리를 잘라내는 것을 가지치기(Pruning)이라고 한다.

유망성을 판단하는 건 명확한 규칙이 있을 때 그 규칙을 위반하는지 검사하는 것이다.

예시 : N-Queen 문제에서 같은 열 혹은 대각선에 퀸이 있으면 안 됨

백트래킹 vs DFS

백트래킹과 DFS는 꽤 비슷하게 느껴지면서 분리하기 애매한 개념이다.

DFS 역시 재귀호출을 통해 다시 시작으로 돌아가는 “뒤로 돌아가기”를 쓰기에 비슷하게 보인다.

하지만 백트래킹은 최적해나 특정 조건을 만족하는 해를 탐색하는 것이 목적이고,
DFS는 그래프의 모든 노드를 방문하는 것이 목적이다.

그렇기에 백트래킹은 가지치기를 통해 일부 경로를 포기하지만 DFS는 모든 경로를 끝까지 다 탐색한다.

백트래킹이 사용되는 대표적인 문제

N-Queen 문제

N-Queen 문제는 백트래킹을 활용하는 대표적인 문제이다.

N × N 체스판 위에 N개의 퀸(Queen) 을 서로 공격하지 않도록 배치하는 문제

규칙은 다음과 같다.

퀸은 같은 행, 같은 열, 같은 대각선 에 놓이면 안 됨.
N개의 퀸을 배치할 수 있는 모든 경우를 찾거나, 가능한 배치 중 하나를 출력.

알고리즘의 흐름은 다음과 같다.

퀸을 한 행씩 배치
1. 이 때 같은 열 or 대각선에 퀸이 존재하면 넘어간다 (가지치기)
배치하면 다음 행으로 이동
마지막 행까지 채웠다면 정답 저장
1. 만약 불가능한 경우라면 이전 단계로 돌아가서 (백트래킹) 1번부터 진행

import sys
input = sys.stdin.readline

# 백트래킹 재귀 함수
def BT(Y):
    global cnt
    if Y > N:
        cnt += 1
        return
    for X in range(1, N+1):
        if not (y[X] or R[X+Y] or L[N-X+Y]):
            y[X] = True; R[X+Y] = True; L[N-X+Y] = True
            BT(Y+1)
            y[X] = False; R[X+Y] = False; L[N-X+Y] = False

N, cnt= int(input()), 0

# y (같은 열 체크) / R (오른쪽 대각선 체크) / L (왼쪽 대각선 체크)
y = [False]*(N+1); R = [False]*(2*N+1); L = [False]*(2*N+1)
BT(1)
print(cnt)

N과 M

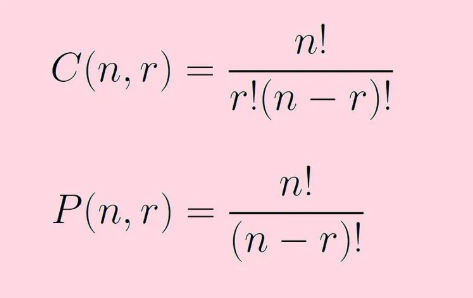
N과 M 문제는 1부터 N까지의 숫자 중에서 길이가 M인 수열을 구하는 문제이다.

종류에 따라 중복 허용 여부와 순서 고려 여부 조건이 다르다.

중복 없이 M개 선택

1부터 N까지의 숫자 중에서 M개를 선택해 나열하는 문제

즉, 순열(Permutation) 문제이다.

import sys
input = sys.stdin.readline

def BT(arr, depth):
    if depth == M:
        for i in range(1, N+1):
            if i not in arr:
                print(*(arr + [i]))
    for i in range(1, N+1):
        if i not in arr:
            BT(arr + [i], depth+1)

N, M = map(int, input().split()); L = []
BT(L, 1)

중복 없이 M 개 선택 (오름차순)

1부터 N까지의 숫자 중에서 M개를 선택하면서 오름차순을 유지하는 문제

즉, 조합(Combination) 문제이다.

import sys
input = sys.stdin.readline

def BT(arr, depth):
    if depth == M:
        for i in range(1, N+1):
            if i not in arr and (i > arr[-1]) if len(arr) != 0 else True:
                print(*(arr + [i]))
    for i in range(1, N+1):
        if i not in arr and (i > arr[-1]) if len(arr) != 0 else True:
            BT(arr + [i], depth+1)

N, M = map(int, input().split()); L = []
BT(L, 1)

중복 허용

1부터 N까지의 숫자 중에서 M개를 선택해 나열하는 문제 (단, 중복 허용)

import sys
input = sys.stdin.readline

def BT(arr, depth):
    if depth == M:
        for i in range(1, N+1):
            print(*(arr + [i]))
    else:
        for i in range(1, N+1):
            BT(arr + [i], depth+1)

N, M = map(int, input().split()); L = []
BT(L, 1)

중복 허용 (오름차순)

1부터 N까지의 숫자 중에서 M개를 선택하면서 오름차순을 유지하는 문제 (단, 중복 허용)

import sys
input = sys.stdin.readline

def BT(arr, depth):
    if depth == M:
        for i in range(1, N+1):
            if (i >= arr[-1]) if len(arr) != 0 else True:
                print(*(arr + [i]))
    else:
        for i in range(1, N+1):
            if (i >= arr[-1]) if len(arr) != 0 else True:
                BT(arr + [i], depth+1)

N, M = map(int, input().split()); L = []
BT(L, 1)

sliver gun

이전 포스트