6장 로지스틱 회귀모델:참 거짓 판단하기

로지스틱 회귀 : 참과 거짓 중 하나를 내놓는 과정

1. 로지스틱 회귀의 정의

ex) 공부 시간에 대한 합격 여부를 판가름하는 경우

로지스틱 회귀는 선형 회귀와 마찬가지로 적절한 선을 그려주는 과정, 다만 직선이 아니라 S자

2. 시그모이드 함수

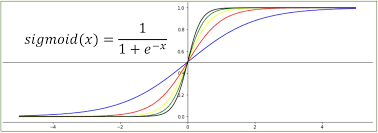
사진의 x를 ax+b로 생각한다....

여기서의 a는 그래프의 경사도, a가 커지면 경사가 커지고 a값이 작아지면 경사가 작아진다.
사진에서는 a가 작으면 파란 곡선, 크면 초록~검은색

b는 그래프의 좌우 이동을 의미, b값이 크고 작아짐에 따라 그래프가 이동
b값이 작으면 오른쪽, 크면 왼쪽에 존재

a값이 작아지면 오차는 무한 대로 커짐 log함수 모양 (오차 그래프)
a가 0에 가까우면 y=a의 그래프

b값이 너무 작은 경우, 이차함수 그래프와 유사한 형태로 나타남.

3. 오차 공식

앞서 배운 경사하강법은 오차를 구한 후, 오차가 작은 쪽으로 이동시키는 방법이었음
이번에도 예측값과 실제 값의 차이, 즉 오차를 구하는 방식이 필요함

시그모이드 함수의 특징이 필요한데 특징은 y의 값이 0과 1사이라는 것
실제 값이 1인데 0에 가까워지면 오차는 커지고 반대로 실제 값이 0일 때 예측 값이 1에 가까워지는 경우에도 오차는 커짐

==> 이 때 필요한 것이 로그 함수

4. 로그함수

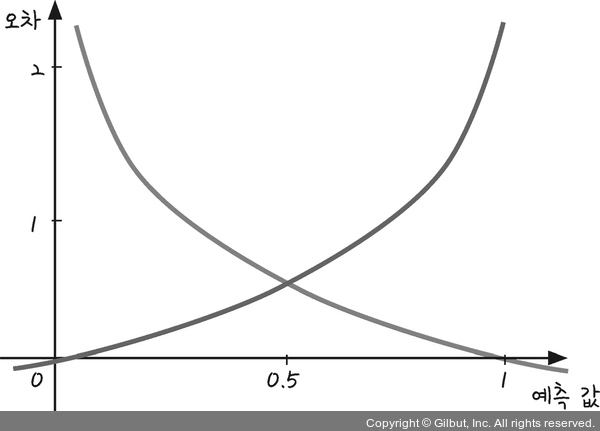
모두의 딥러닝 사진에서 퍼옴

위에서 아래로 내려오는게 파란색, 아래에서 위로 올라가는게 빨간색

파란선은 실제 값이 1일 때, 사용하는 그래프 예측 값이 1일 때 오차가 0이고 반대로 예측이 0에 가까울수록 오차는 커짐
빨간 선은 반대로 실제 값이 0일 때 사용하는 함수 예측 값이 0일 때 오차가 없고 1에 가까워질수록 오차가 매우커짐

그래프는 각각 파란색: -logh 빨간색 -log(1-h)
실제 값이 1일때는 -logh를 쓰고 0일 때는 -log(1-h)를 쓴다.

==> -{ylogh +(1-y)log(1-h)} 실제 값이 y라면 값이 1이면 B부분이 없어짐. 반대로 0이면 A부분이 없어진다. 이 함수를 머신러닝에서는 교차 엔트로피 오차 라고 합니다.

선형회귀 <= 평균제곱 오차, 로지스틱 회귀 <= 교차 엔트로피 오차

5. 텐서플로에서 실행하는 로지스틱 회귀모델

선형회귀와 비슷한데 다른 점은 손실함수가 평균 오차 제곱함수에서 크로스 엔트로피 오차로 바뀌는 것

x = np.array([2,4,6,8,10,12,14])
y = np.array([0,0,0,1,1,1,1]) #합격 여부 데이터

시그모이드를 사용하므로 activation부분을 sigmod로 바꿔줌

기타 설정을 바꿔준다.

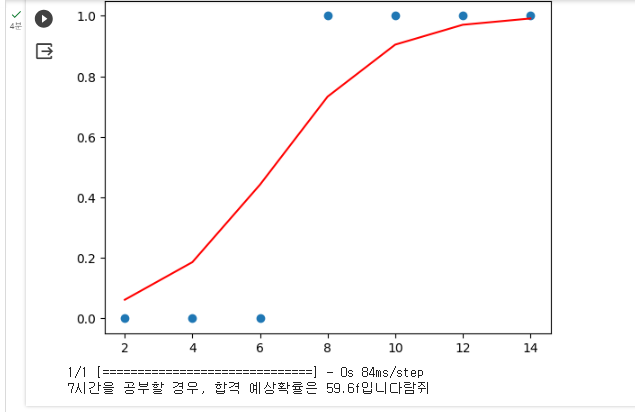
그래프를 자세히 보면 시그모이드 함수 그래프의 형태를 취하게 된다.
학습 시간이 7보다 클 경우에는 합격 확률이 50%가 넘는다.

다양한 요소를 추가함에따라 정확도는 향상된다. 굳