🔗 이 포스트에 대해 더 궁금하신가요? 다음 주소를 참고해주세요!
🗒️ 이 글의 수정 내역 (마지막 수정 일자: 없음)
🚀 시작하며
드디어 대망의 최적화 이전의 로직을 모두 구현하게 되어 기분이 좋아요! (오열)
마지막으로 메타볼을 융합하는 로직을 만들 건데요. 이는 생각보다 쉽지 않아요.
차근차근 설명할 예정이니, 따라오시죠! 🙆🏻♀️
알고리즘 설계
일단 융합에 있어서 가장 필요한 것은, 어떻게 설계하는지에 관한 것이에요.
최적화 이전, 당시에는 다음과 같이 판단했습니다.
- 1픽셀씩 전체 화면의
width,height를 나누어주자. - 각 픽셀마다, 해당 픽셀에서 갖고 있는 어떤 특정한 역치를 초과하면 융합되듯이
fillColor한다. - 렌더링을 진행한다.
여기서 중요한 것은 2번입니다.
어떻게 특정한 역치를 산정할 수 있을까요? 사실 메타볼을 만들 때 가장 고민했던 부분이 이 부분입니다.
원의 방정식을 활용하라
이 글에서 많은 영감과 도움을 받았습니다.
메타볼을 만드는 데 있어, 결과적으로 원의 방정식을 활용하는 것이죠.
우리의 원을 픽셀이라는 개념으로 말하면 어떻게 말할 수 있을까요?
x, y라는 포지션에서 일정 거리의 반지름 r 안에 있는 모든 픽셀을 원이라 할 수 있죠.
그렇다면, 이는 다음과 같은 공식을 만족합니다.
픽셀의 위치를
a, b라 할 때 이 픽셀이 원 안에 들어와 있다면
(a - x) ^ 2 * (b - y) ^ 2 <= r ^ 2
즉, 만약 r이 어떤 핵으로부터 핵이 가지는 영향력이라고 본다면, 핵의 영향력은 거리의 크기에 반비례함을 알 수 있죠.
이는 실제로 Wikipedia - metaball에도 명시되어 있듯, 역제곱 법칙이 성립한다고 할 수 있습니다.
즉, 임계값을 1이라고 칠 때, 이 값은 그 주변에 존재하는 메타볼들의 r ^ 2 / ((a - x) ^ 2 * (b - y) ^ 2)값들보다 크면 되는 것이죠!
이것이 의미하는 것은, r이라는 게 핵의 영향력이라면
- 주변의 핵이 가진 영향력 역시 반영해야 하기에 이를 각 메타볼마다 구해야 합니다.
- 이들을 모두 합한 결과는 그 위치에서 메타볼이 영향력을 가지는 세기이죠.
- 그리고 그 세기가 1보다 크다는 것은 특정 원의 내부가 가지는 세기의 최소 요건(임계값 이상)을 만족하는 것이죠.
- 따라서 융합을 할 수 있다고 판단하여 색을 칠하게 되는 것이죠!
저 역시 이쪽 전문은 아니다 보니(...) 아무래도 부족한 설명이라 이해가 됐을런지 모르겠네요.
혹시나 더 궁금하시다면, 위에서 첨부한 위키피디아를 참고하시는 게 더욱 객관적이라 보입니다 😉
그렇다면, 이제 전략을 구현하러 가볼까요?
FuseStrategy
function shouldFuse(
balls: (DynamicMetaball | StaticMetaball)[],
cx: number,
cy: number,
) {
const total = balls.reduce((forceSum, ball) => {
const {x, y, r} = ball;
const acc = forceSum + r ** 2 / ((cx - x) ** 2 + (cy - y) ** 2);
return acc;
}, 0);
return total >= 1;
}
export class FuseStrategy implements Strategy {
before?: (...args: unknown[]) => void;
after?: (...args: unknown[]) => void;
constructor() {}
setBefore(callback: (...args: unknown[]) => void) {
this.before = callback.bind(this);
}
setAfter(callback: (...args: unknown[]) => void) {
this.after = callback.bind(this);
}
exec(ctx: Canvas['ctx'], balls: (DynamicMetaball | StaticMetaball)[]) {
this.before?.();
const {innerWidth, innerHeight} = window;
for (let cx = 0; cx < innerWidth; cx += 1) {
for (let cy = 0; cy < innerHeight; cy += 1) {
if (shouldFuse(balls, cx, cy)) {
ctx.save();
ctx.fillStyle = '#ffaa00';
ctx.fillRect(cx, cy, 1, 1);
ctx.restore();
}
}
}
this.after?.();
}
}구현이 단순하다 보니, 생각보다 큰 시간이 소요되지 않았어요. 🙆🏻🙆🏻♀️
다만, 이제 주의할 게 있어요.
엇, 기존 메타볼들끼리는 어떻게 비교해야 하나요?
설계에 있어 이게 가장 고민이 되었어요. 😖
이유는, Metaball을 각각 비교하는 게 아니라, Canvas 자체에서 각 픽셀들의 영향력을, Observers가 갖고 있는 각각의 메타볼들의 거리를 기준으로 합산하여 계산하기 때문입니다.
즉, 대상이 픽셀이 되어버리기 때문에 기존처럼 Observer에 알고리즘을 넣어줄 수 없는 거에요.
이럴 때에는 차분하게, 무엇이 필요한지를 생각해보면 돼요.
우리가 필요한 것은
- 메타볼들에 대한 모든 데이터
- 거리에 따라 결과를 그려내는 것
이죠?!
따라서 이 2개를 그려내기 위해 App에서 ctx와 allMetaballs를 꺼내줍시다.
AnimationSubject.ts
export class AnimationSubject implements MetaballsSubject {
// 기존 코드 생략 ...
get allMetaballs() {
const arr: (StaticMetaball | DynamicMetaball)[] = [];
const allBalls = [...this.observers].map(observer => observer.metaballs);
allBalls.forEach(balls => {
arr.push(...balls.balls);
});
return arr;
}
}Canvas.ts
export class MetaballCanvas implements GradientCanvas {
// 기존 코드 생략...
get allMetaballs() {
return this.metaballAnimationSubject.allMetaballs;
}App.ts
export class MetaballAnimation implements CanvasAnimation {
// 기존 코드 생략...
get canvasCtx() {
return this.canvas.ctx;
}
get allMetaballs() {
return this.canvas.allMetaballs;
}
}이제 이를 외부에서 세팅하면 끝나겠죠?!
이때, 모든 것을 다 그린 후에, 융합되는 로직을 그려내면 됩니다.
💡 잠깐! 그런데 우리는 어디에서 이 전략을 넣어야 하죠?! 클래스 내부에서는 넣어주는 곳이 없잖아요!
맞아요. 이럴 때 유연하게 쓰기 위해, 저는 전략에 before와 after이라는 메서드를 넣어주었죠. 😄
항상 앞으로 어떤 것이 예상될지를 생각하고, 몇 줄 간단한 정도의 코드만 더 작성해주면 이렇게 당황스러운 일에도 잘 대처할 수 있게 돼요. 저 역시 혹시나 해서 설계를 기존처럼 미리 했었는데, 확장성을 고려한 설계에 대한 보람을 간만에 느꼈어요!
이후 생성에 관한 메인 & 전역 로직들을 모두 적어둘게요.
App.ts
const $target = document.body;
const {innerWidth, innerHeight} = window;
const app = new MetaballAnimation({
canvas: new MetaballCanvas({
gradients: ['#123141', '#235234'],
width: innerWidth,
height: innerHeight,
type: ECanvasGradientType.linear,
options: {
autoplay: true,
},
}),
dataset: {
dynamic: Array.from({length: 4}, (_, idx) => {
const rate = 0.1 * (idx + 1);
return {
x: innerWidth * rate,
y: innerHeight * rate,
r: 300 * rate,
v: {x: 10 * rate, y: 1 / rate},
vWeight: 1 * rate,
};
}),
},
});
function main() {
const moveStrategy = new MoveStrategy();
const drawStrategy = new DrawStrategy();
const fuseStrategy = new FuseStrategy();
app.setDynamicMetaballMove({
moveStrategy,
key: EMetaballObserverKeys.dynamic,
});
app.setDynamicMetaballDraw({
drawStrategy,
key: EMetaballObserverKeys.dynamic,
});
drawStrategy.setAfter(() => {
fuseStrategy.exec(app.canvasCtx, app.allMetaballs);
});
app.mount($target);
}
main();결과
잘 작동하는군요!

최적화 이전의 장단점 분석
일단 장점 먼저 말씀드리자면, 사실상 완전 탐색이니 가장 정확합니다.
현재 최적화 이전의 로직은 가장 메타볼의 구현 로직을 충실히 따르기 때문에, 융합했을 때 도형이 커지는 현상, 융합하는 현상이 가장 자연스러워요.
다만 단점이 있다면, 지금 보이는 애니메이션처럼 성능이 매우 느립니다.
이를 Chrome에서 10초간 재생했을 때 발생하는 퍼포먼스 비용을 한 번 살펴볼게요.
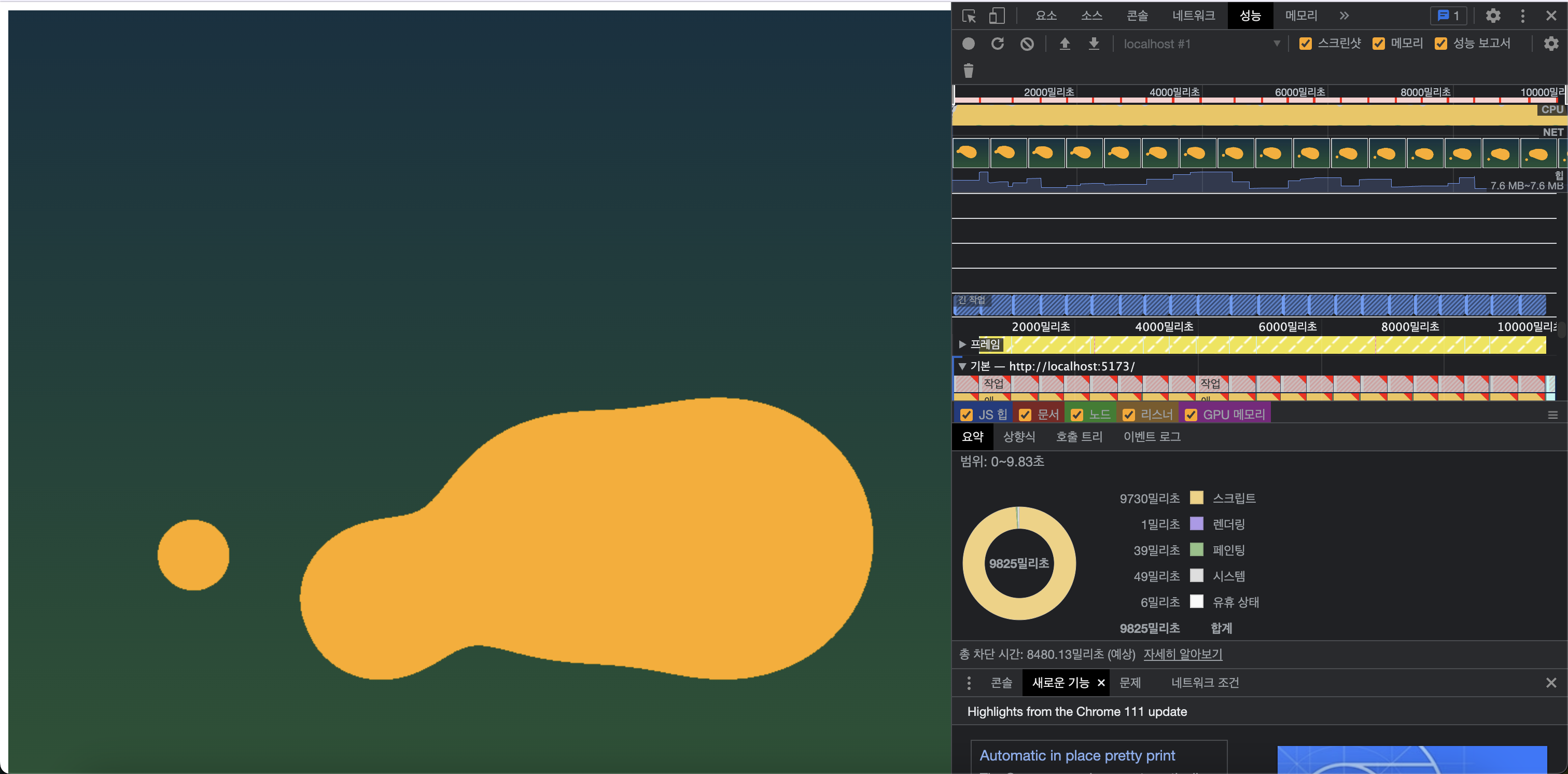
렌더링, 페인팅에 관해서는 빠르게 되어 있는데요! 스크립트 처리 속도가 거의 97%를 차지하는 군요.
(또한, 실제로는 스크립트가 유휴상태를 다 차지해버렸으니, 이 역시 아직 빠르다고 판단하기는 이릅니다.)
네. 이 알고리즘의 단점은 굉장히 느립니다.
실제로 drawStrategy의 exec 메서드는 FuseStrategy까지 합하여 꽤나 많은 렌더링을 차지하고 있어요. 약 2418ms를 차지하고 있네요.
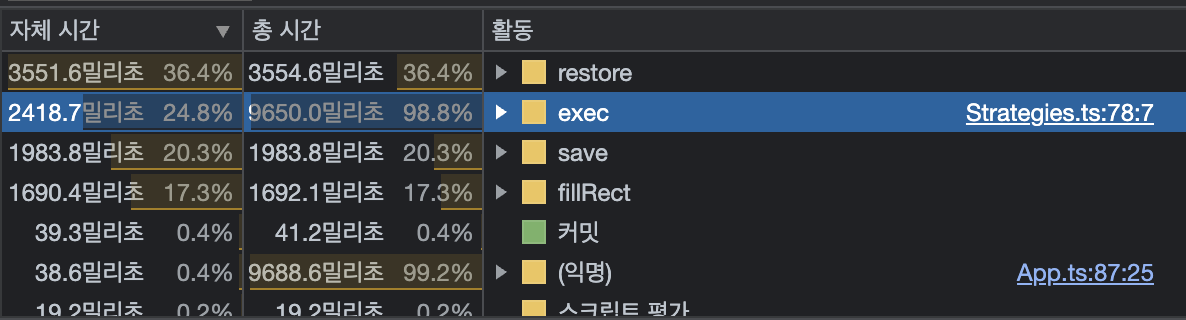
컨텍스트 정보를 restore한 것에 대한 비용이 생각보다 많아 이를 한 번 주석처리하고 렌더링을 해보겠습니다.

유휴 상태는 아주 조금 생기기 시작했지만, 실제로 연산은 매우 과하며

확실히 여유공간이 생기니, 페인팅에 대한 비용이 증가한 것을 확인할 수 있죠!
이는 픽셀 전체를 일일이 하나씩 fill하기 때문에 발생한 비용임을 짐작할 수 있습니다.
따라서 결론은 다음과 같아요.
실제로 페인팅과 각 픽셀 전체를 완전탐색하는 알고리즘의 시간 복잡도가 높기 때문에 실제로 사용하기 어렵다.
🎉 마치며
휴! 드디어 최적화 이전의 로직을 짜는 포스트를 마쳤네요.
사실 짜는 건 어렵지 않은데, 아무래도 더 좋은 코드를 설계하고자 하는 욕심에 더 많이 생각하느라 구현이 늦은 감이 있었네요!
그렇지만 더 안정적인 설계를 완료했으니, 이에 관련한 최적화 글 역시 더 빠르게 업데이트할 수 있지 않을까요? 😉
미리 스포를 드리자면, 이제 시리즈로 연재할 <최적화 이후 메타볼 애니메이션 포스트>에서는 다음을 포기합니다.
- 메타볼이 합칠 때 더이상 커지지 않아요.
- 합치는 로직이 살짝 부자연스러워요.
대신 다음을 획득할 수 있어요.
- 어림잡아 약 20배의 성능을 개선할 수 있어요.
- 벡터를 사용하기에 메타볼이 융합하는 과정에서 발생하는 매끄럽지 않은 선들을 개선할 수 있어요.
힌트를 미리 드리자면, PaperJS - Meta Ball로부터 많은 영감을 받았어요. 😉
메타볼 2D 애니메이션을 만드시려던 분들께, 좋은 도움이 되는 포스트가 된다면 좋겠네요. 이상!
참고자료
메타볼 분석에 관한 도움을 얻었던 글
Wikipedia - metaball
PaperJS - Meta Ball
.jpg)