Red-Black Tree

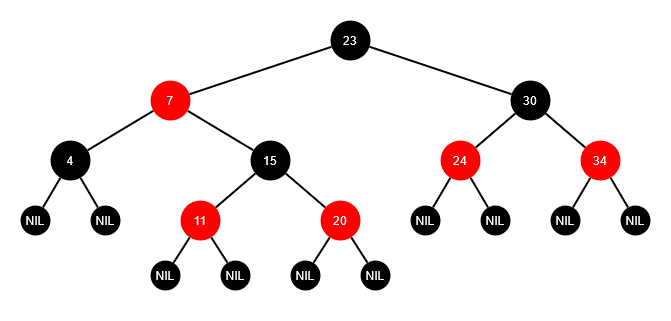
• 이진탐색트리(BST) 의 한 종류
• 스스로 균형(balancing) 잡는 트리
• BST의 worst case(한쪽으로 편향되어 있는 case) 단점을 개선
• 모든 노드는 RED 혹은 BLACK

nil 노드란?

• 존재하지 않음을 의미하는 노드
• 자녀가 없을 때 자녀를 nil노드로 표기
• 값이 있는 노드와 동등하게 취급
• RB트리에서 leaf 노드는 nil 노드

RB트리 속성

1. 모든 노드는 RED 혹은 BLACK
2. 루트 노드는 BLACK
3. 모든 nil 노드는 BLACK
4. RED의 자녀들은 BLACK 또는 RED가 연속적으로 존재할 수 없다.
5. 임의의 노드에서 자손 nil 노드들까지 가는 경로들의
   BLACK수는 같다. (자기 자신은 카운트에서 제외)
6. 임의의 노드에서 자손 nil노드들 까지 가는 경로들의 BLACK 수는 같다.(5번 속성을 만족해야 성립하는 개념)

색을 바꾸면서도 5번 속성을 유지하기

• RB트리가 5번속성을 만족하고 있고, 두 자녀가 같은 색을 가질 때 부모와 두 자녀의 색을 바꿔줘도 5번 속성은 여전히 만족한다.

RB 트리는 어떻게 균형을 잡는가?

• 삽입/삭제 시 주로 4번속성과 5번속성을 위반하며, 이들을 해결하려고 구조를 바꾸다보면 자연스럽게 트리의 균형이 잡히게 된다.

---

RB트리 삽입

• 삽입 전 RB 트리 속성을 만족한 상태여야함
• 삽입 방식은 일반적인 BST와 동일
• 삽입하는 노드는 RED여야함 (삽입 후에도 5번속성을 만족하기 위해)
• 삽입 후 RB트리 위반 여부 확인
• RB트리 속성을 위반했다면 재조정
• RB트리 속성을 다시 만족

삽입 예제

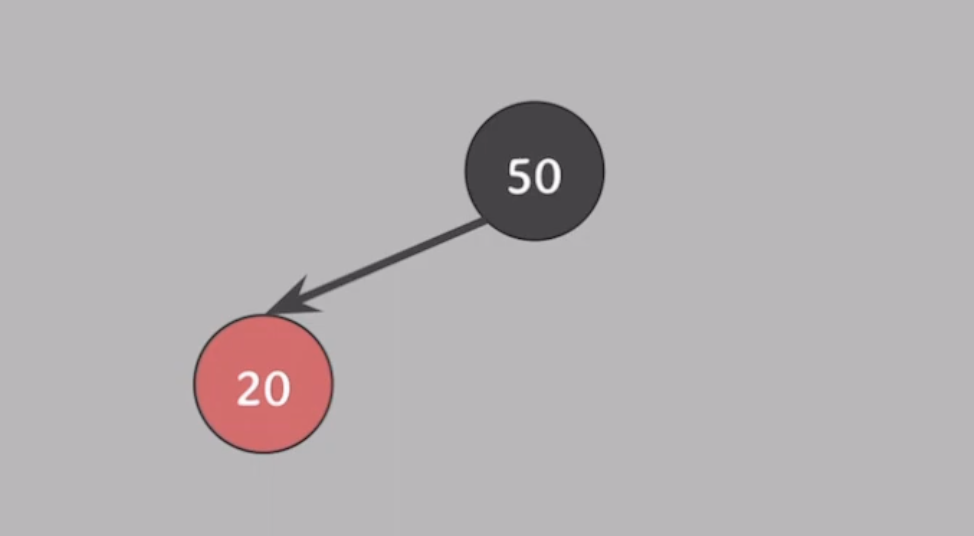이 트리에 10을 넣어보자. 1. 10과 50비교, 10과 20을 비교해서 20 왼쪽에 10이 들어가게 됨. 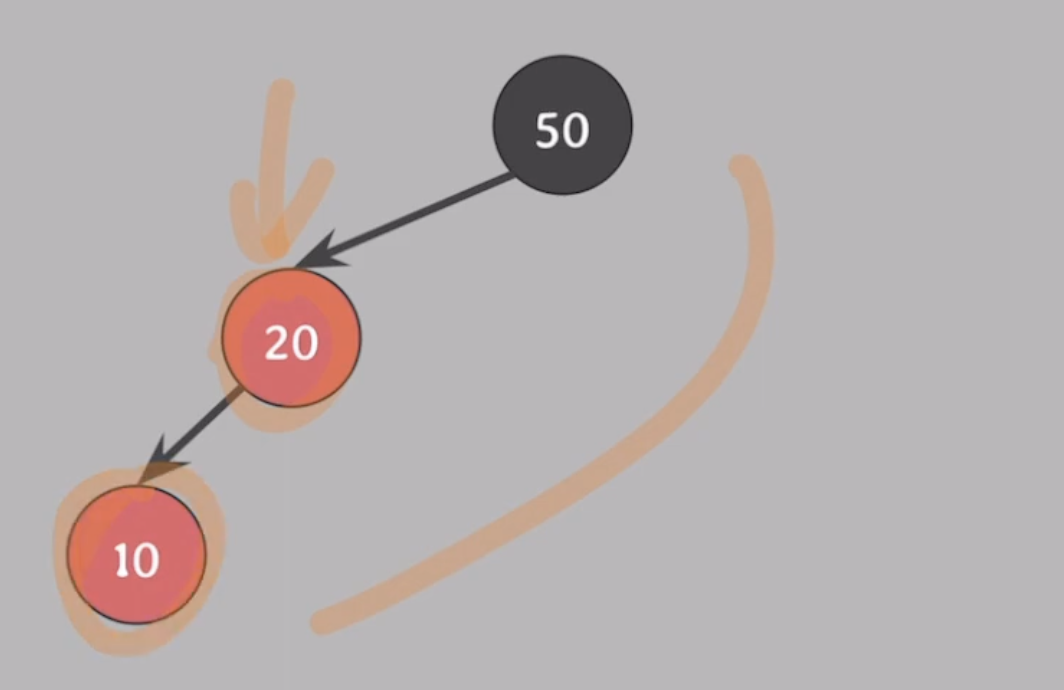여기에서 4번 속성 위반.(# 4: 노드가 RED라면 자녀들은 BLACK) 이 문제를 해결하기 위해 RED가 한쪽으로 몰려 있으니 RED하나를 반대편으로 옮겨준다. 잊지 말아야 할것은 구조를 바꿔준 뒤에 BST 특징 또한 유지되어야 한다.

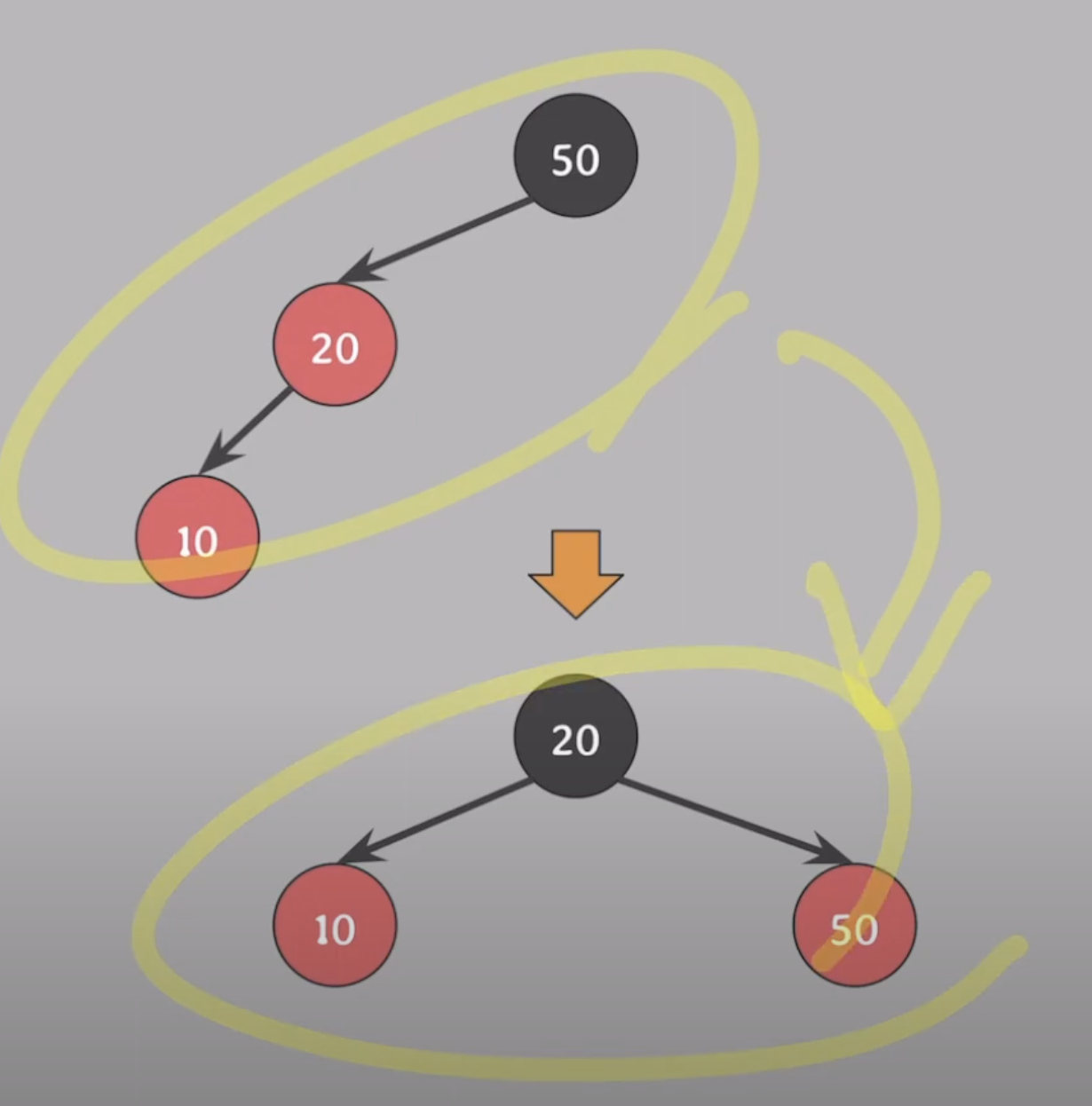
4번 속성을 위반한 상태인데, 해결하기 위해 RED하나를 넘겨야 하는데 BST특징 또한 유지하면서 넘기려면 회전을 사용해야 한다.

해결방법 & 정리

1. 20 과 50의 색을 바꿔준다.
2. 50을 기준으로 오른쪽으로 회전한다.

• 삽입된 RED노드가 부모의 왼쪽 자녀이면서
  부모도 RED고 할아버지의 왼쪽 자녀와 삼촌은 BLACK 이라면
  부모와 할아버지의 색을 바꾼 후 할아버지 기준으로 오른쪽으로 회전한다
  ( 왼쪽과 오른쪽을 바꾸면 반전된 경우에도 성립됨)

---

삽입 예제 2

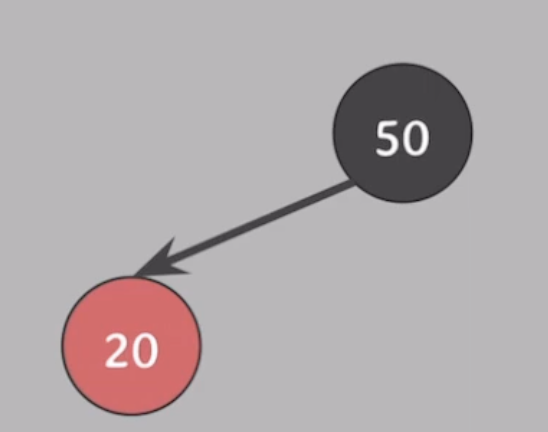40을 넣어보자.
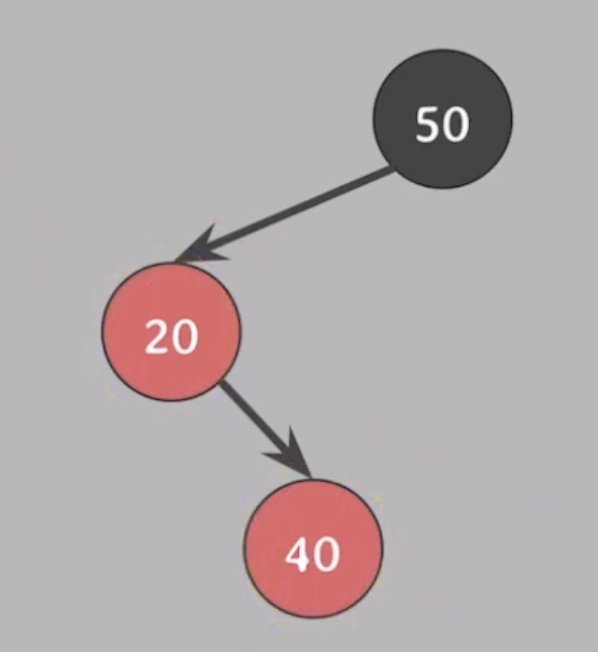20에 오른쪽에 삽입되고 4번 속성 위반됨.

4번 속성 위반을 해결하기 위해 RED 하나를 넘겨야 하는데, 앞의 경우와 다른 점은 삽입된 노드를 기준으로 할아버지까지의 경로가 꺾였다 는 점.
꺾인 부분을 펴줘서 앞 경우와 같이 만들면 된다.

해결 방법

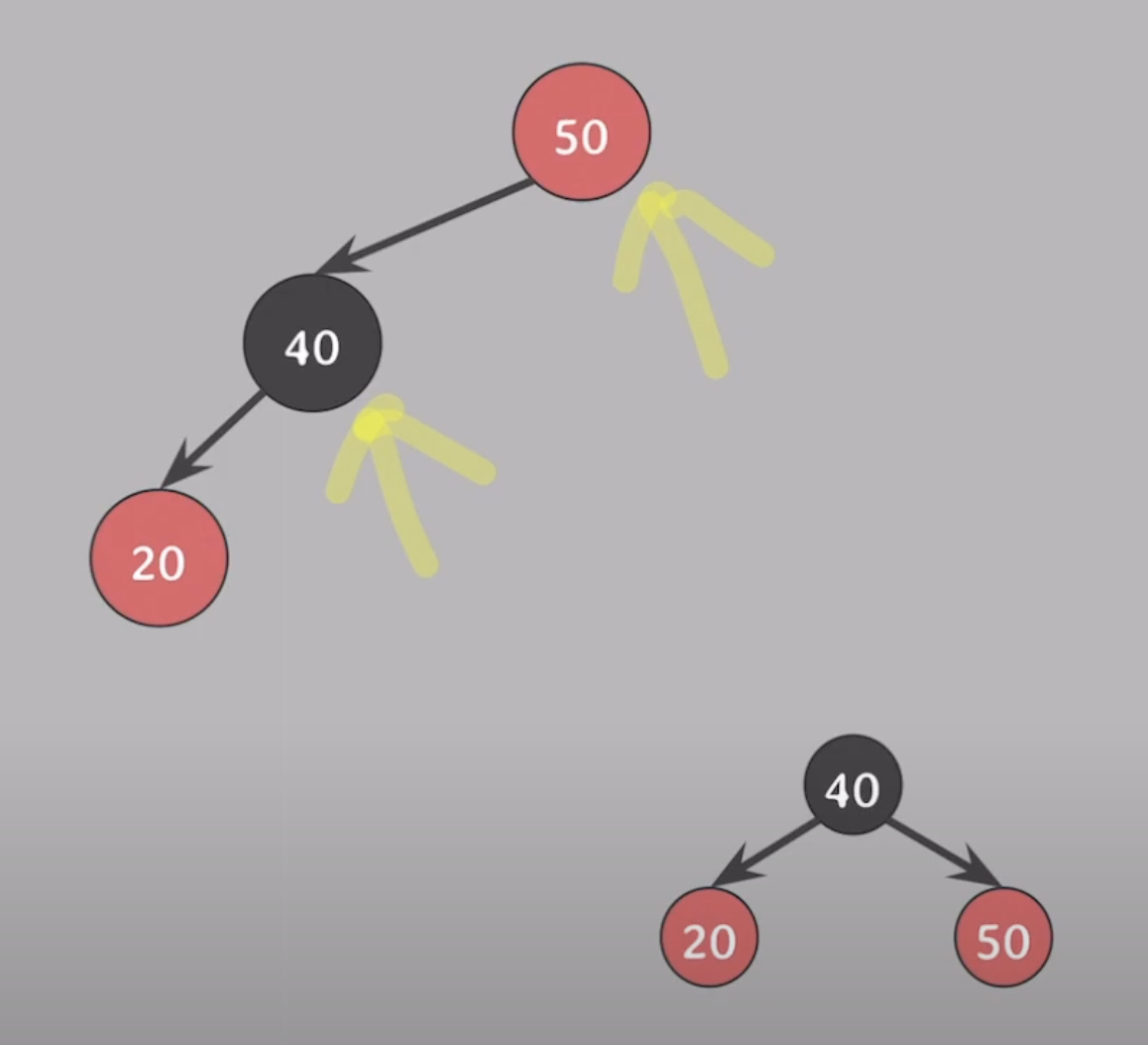
1. 20 기준으로 왼쪽으로 회전 (40과 20의 위치가 바뀌게됨)
2. 40과 50의 색을 바꾼다.
3. 50 기준으로 오른쪽 회전

정리

• 삽입된 RED 노드가 부모의 오른쪽 자녀이며
  부모도 RED고 할아버지의 왼쪽 자녀와 삼촌은 BLACK이라면
  부모를 기준으로 왼쪽으로 회전한 뒤 예제1 방식대로 해결
  ( 왼쪽과 오른쪽을 바꾸면 반전된 경우에도 성립됨)

---

삽입 예제 3

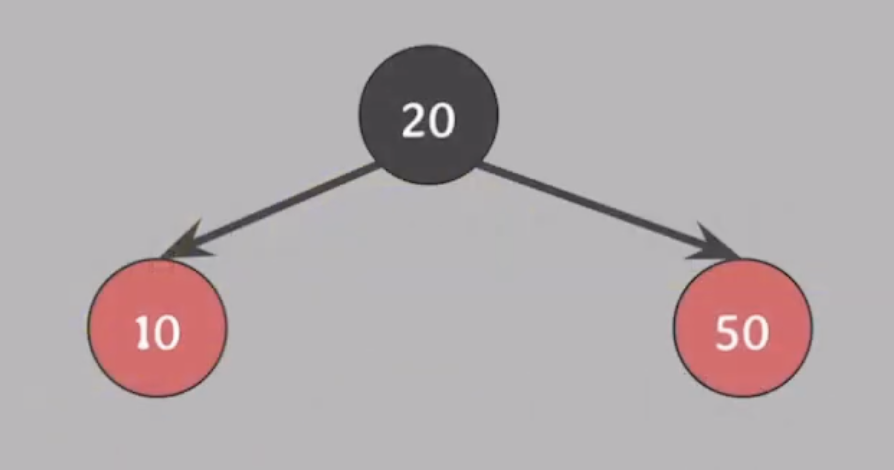30을 삽입해보자 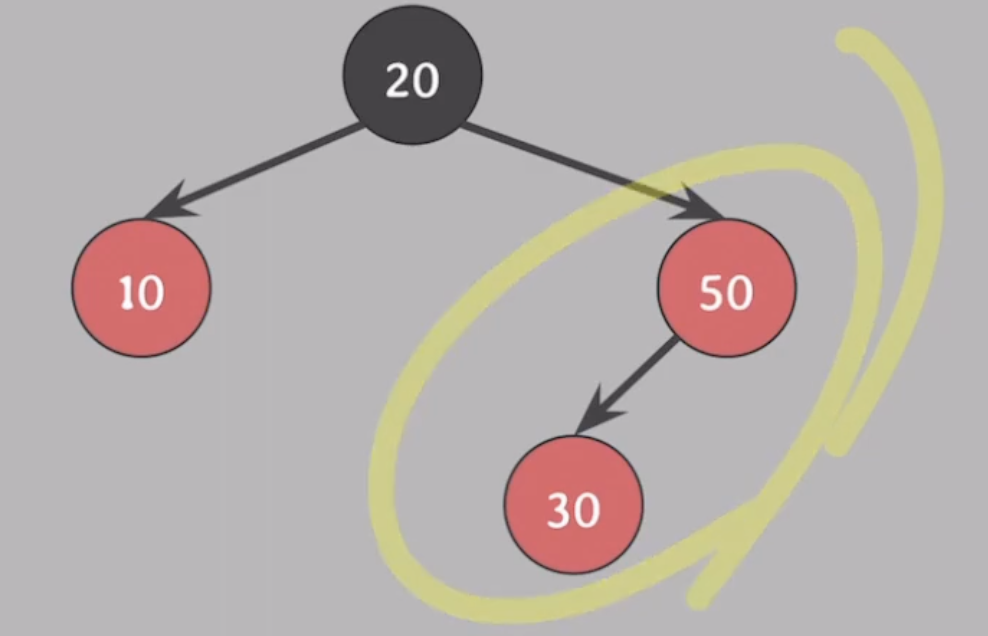#4를 만족시키면서 #5를 유지하려면 10과 50을 바꾸고 20을 RED로 바꾸면된다. 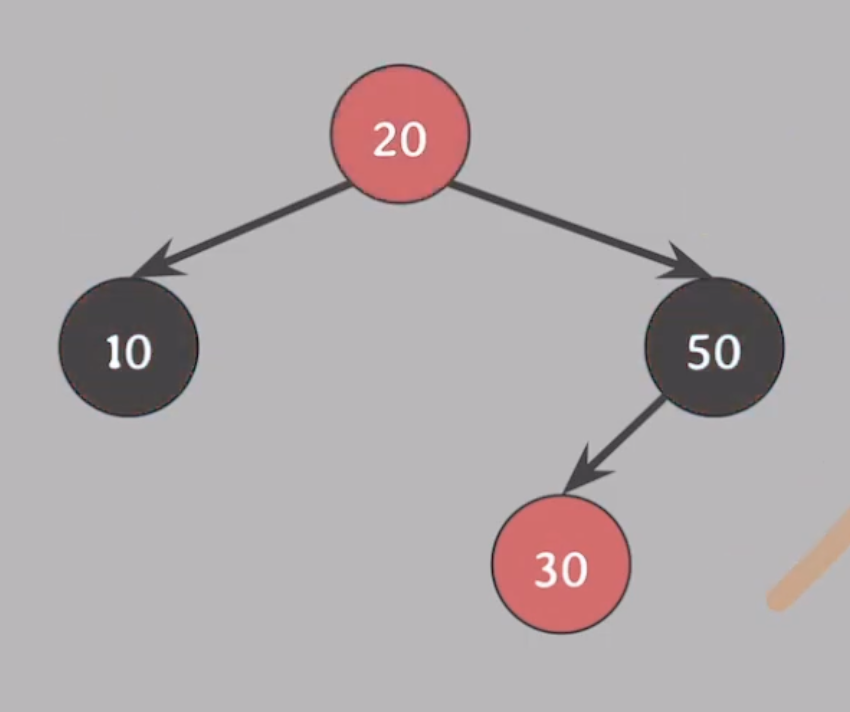20이 루트노드라서 #2 속성(루트노드는 블랙) 을 위반함. 20을 BLACK으로 바꿔주자.

해결 방법

• 삽입된 RED노드의 부모도 RED이고 삼촌도 RED라면
  부모와 삼촌을 BLACK으로 바꾸고 할아버지를 RED로 바꾼 뒤 할아버지에서 다시 확인 시작

---

구현하기 ( C )

Left Rotate

void left_rotate(rbtree *t, node_t *p){
  // p의 오른쪽에 y노드 지정
  node_t *y = p->right;
  // y노드의 왼쪽노드를 p노드의 오른쪽으로 옮긴다.
  p->right = y->left;
  // y노드의 왼쪽노드에 노드가 존재한다면
  // 그 노드의 부모값을 x로 지정한다.
  if(y->left != t->nil){
    y->left->parent = p;
  }
  // y의 부모값을 p의 부모값으로 지정하여 원래 p가 있던 자리에 y를 넣어준다.
  y->parent = p->parent;
  // p가 root인 경우
  if (p->parent == t->nil){
    // 트리의 루트를 y로 지정해준다.
    t->root = y;
  // p가 왼쪽 자식인 경우
  }else if (p == p->parent->left){
    // p부모의 왼쪽노드를 y라고 해준다.
    p->parent->left = y;
  // p가 오른쪽 자식인 경우
  }else{
    //p부모의 오른쪽 노드를 y라고 해준다.
    p->parent->right = y;
  }
  //y의 왼쪽자식과 p의 부모노드 update
  y->left = p;
  p->parent = y;
}

Right Rotate

void right_rotate(rbtree *t, node_t *p){
  node_t *y = p->left;
  p->left = y->right;
  if(y->right != t->nil){
    y->right->parent = p;
  }
  y->parent = p->parent;
  // p == root
  if (p->parent == t->nil){
    t->root = y;
  // p == right
  }else if (p == p->parent->right){
    p->parent->right = y;
  //p == left
  }else{
    p->parent->left = y;
  }
  y->right = p;
  p->parent = y;
}

Insert

node_t *rbtree_insert(rbtree *t, const key_t key) {
  // 트리의 nil노드에 해당하는 y노드 생성
  node_t *y = t->nil;
  //트리의 루트에 해당하는 x노드 생성
  node_t *x = t->root;
  node_t *z = (node_t *)calloc(1, sizeof(node_t));
  z->key = key;
  //x 값이 nil 아닐때까지 탐색
  while(x != t->nil){
    // x가 nil을 만나기 전값을 y에 기록
    y = x;
    if(z->key < x->key){
      x = x->left;
    }else{
      x = x->right;
    }
  }
  z->parent = y;
  if (y==t->nil){
    t->root = z;
  }else if(z->key < y->key){
    y->left = z;
  }else{
    y->right = z;
  }
  z->left = t->nil;
  z->right = t->nil;
  z->color = RBTREE_RED;

  // fix up 
  while (z->parent->color == RBTREE_RED){
    // new node의 부모노드가 왼쪽 자식인 경우
    if(z->parent == z->parent->parent->left){
      // 부모 노드의 형제 노드
      y = z->parent->parent->right;
      // 경우 1 : 삼촌 색이 RED
      if (y->color == RBTREE_RED){
        z->parent->color = RBTREE_BLACK;
        y->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        z = z->parent->parent;
      // 경우 2 && 3 : 삼촌 색이 BLACK
      }else{
        // 경우 2
        if(z == z->parent->right){
          z = z->parent;
          left_rotate(t,z);
        }
        //경우 3
        z->parent->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        right_rotate(t, z->parent->parent);
      }
    }else{ //new node의 부모노드가 오른쪽 자식일 경우
      // 삼촌 노드 정의
      y = z->parent->parent->left;
      // 경우 4 : 삼촌 RED
      if (y->color == RBTREE_RED){
        z->parent->color = RBTREE_BLACK;
        y->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        z = z->parent->parent;
      }else{
        // 경우 5 && 6
        if(z == z->parent->left){
          z = z->parent;
          right_rotate(t,z);
        }
        z->parent->color = RBTREE_BLACK;
        z->parent->parent->color = RBTREE_RED;
        left_rotate(t, z->parent->parent);
      }
    }
  }
  t->root->color = RBTREE_BLACK;
  return z;
}

참고자료
https://www.youtube.com/watch?v=2MdsebfJOyM