Red Black Tree 의 삭제 방식
- 삭제 전 RB 트리 속성 만족한 상태
- 삭제 방식은 일반적인 BST와 동일
- 삭제 후 RB 트리 속성 위반 여부 확인
- RB 트리 속성을 위반했다면 재조정
- RB 트리 속성을 다시 만족
삭제되는 색을 통해 속성 위반 여부 확인
- 삭제하려는 노드의 자녀가 없거나 하나라면 삭제되는 색은 삭제되는 노드의 색
- 삭제하려는 노드의 자녀가 둘이라면 삭제되는 색은 삭제되는 노드의 successor의 색
- 삭제되는 색이 RED라면 어떠한 속성도 위반하지 않는다.
- 삭제되는 색이 BLACK일때 대부분의 경우에는 5번속성을 위반하게 된다.
삭제되는 색이 Black이고 #5 위반일 때
- 경로에서 Black수를 카운트할때
extra black은 하나의 black으로 카운트 된다. - 삭제된 색의 위치를 대체한 노드인 nil노드에
extra black을 부여하면 #5 속성을 다시 만족함 doubly-black: extra black이 부여된 BLACK 노드Red-and-Black: extra black이 부여된 RED노드
Red and Black 해결하기
- Red-and-Black 을 Black으로 바꾸면 해결
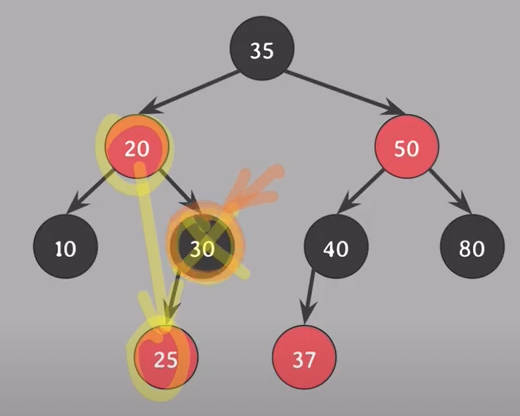
- 30은 자녀가 하나라서 삭제되는 색은 30의 BLACK (#5 위반)
- 20과 25가 바로 연결 (#4 위반)
- 삭제된 색은 30의 BLACK이었고, 30을 대체하는 25의 RED에
extra black부여 - 25가
red-and-black이 되었으니 25를 BLACK으로 바꿔주면 종료
Doubly-Black 해결하기
- 결국 extra black을 어떻게 없앨건지가 관건
- 네가지 CASE로 분류할 때의 기준은
doubly-black의 형제의 색과 그 형제의 자녀들의 색
CASE A
doubly-black의 오른쪽 형제가BLACK이고 그 형제의 오른쪽 자녀가RED일 때그 RED를
doubly-black위로 옮기고 옮긴 RED로extra black을 전달해서red-and-black으로 만들면 BLACK으로 바꾸고 해결
CASE B
doubly-black의 오른쪽 형제가 BLACK이고, 그 형제의 왼쪽 자녀가 RED 이면서 그 형제의 오른쪽 자녀는 BLACK일때doubly-black의 형제의 오른쪽 자녀가 RED가 되게 만들어서 이후엔 case A를 적용하여 해결
CASE C
doubly-black의 형제가 BLACK이고, 그 형제의 자녀가 모두 BLACK일때doubly-black과 그 형제의 BLACK을 모아서 부모에게 전달해 부모가extra-black을 해결하도록 위임
CASE D
doubly-black의 형제가 RED일때doubly-black의 형제를 BLACK으로 만든후 CASE A,B,C중 하나로 해결
정리
- 삭제되는 색이 BLACK일때, 삭제되는 색이 있던 위치를 대체한 노드에
extra-black을 부여한다. - 대체한 노드가
red-and-black이 되었다면 BLACK으로 바꿔줌 - 대체한 노드가
doubly-black이 되었다면 case A, B, C, D중에 하나로 해결
RB트리의 시간 복잡도
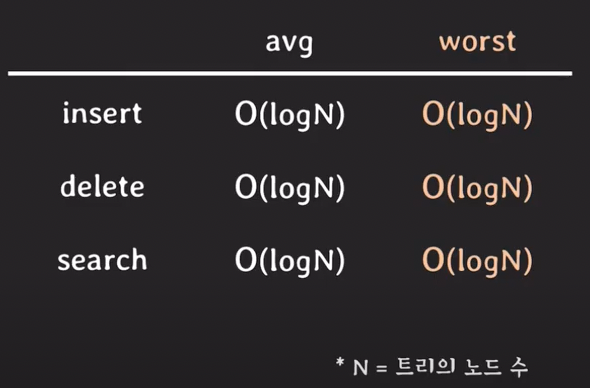
구현 (C)
// 이식하는 함수
// 서브 트리 이동을 위해 노드가 u가 루트인 서브트리를 노드 v가 루트인 서브트리로 교체
void transplant(rbtree *t, node_t *u, node_t *v){
if (u->parent == t->nil){ // u의 부모가 nil 즉, u가 루트노드라면
t->root = v; //v를 트리의 루트노드로 삼는다.
}else if(u == u->parent->left){ //u가 부모의 왼쪽 자식일 경우
u->parent->left = v; //v를 왼쪽 자식으로 이식 (u를 대체)
}else{ //오른쪽 자식일 경우
u->parent->right = v; //v를 오른쪽 자식으로 이식
}
v->parent = u->parent;
}int rbtree_erase(rbtree *t, node_t *z) {
// 삭제하려는 노드 z를 우선 y에 저장.
// y가 z를 기준으로 시작하지만 중간에 바뀔 수 있다.
node_t *y = z;
node_t *x;
color_t y_original_color = y->color;
// 노드 z에게 유효한 값을 가진 자식이 하나 있는데
// 그 자식이 오른쪽에 있는 경우
if (z->left == t->nil){
x = z->right; //오른쪽 자식을 x에 담아두고
transplant(t, z, z->right); //z의 오른쪽 자식을 p에 위치에 이식(transplant)하면서 z는 제거
//유효한 값을 가진 자식이 왼쪽에만 하나 있는 경우
}else if(z->right == t->nil){
x = z->left;
// z의 왼쪽 자식을 z에 위치에 이식하면서 p는 제거됨
transplant(t, z, z->left);
}else{
// 유효한 자식이 둘인 경우
y = tree_minimum(t, z->right);
y_original_color = y->color;
x = y->right;
if (y->parent == z){
x->parent = y;
}else{
transplant(t, y, y->right);
y->right = z->right;
y->right->parent = y;
}
transplant(t, z, y);
y->left = z->left;
y->left->parent = y;
y->color = z->color;
}
// 삭제되는 색이 BLACK인 경우에만 속성 위반 여부 확인
// fix up
if (y_original_color == RBTREE_BLACK){
node_t *w;
while (x!=t->root && x->color == RBTREE_BLACK){
if(x == x->parent->left){
w = x->parent->right;
// x 의 형제 w가 RED 인 경우
if(w->color == RBTREE_RED){
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
left_rotate(t, x->parent);
w = x->parent->right;
}
// X의 형제 W는 BLACK이고 W의 두 자식이 모두 BLACK인 경우
if(w->left->color == RBTREE_BLACK && w->right->color==RBTREE_BLACK){
w->color = RBTREE_RED;
x = x->parent;
// X의 형제 W는 BLACK, W의 왼쪽 자식은 RED, W의 오른쪽 자식은 BLACK인 경우
}else{
if(w->right->color == RBTREE_BLACK){
w->left->color = RBTREE_BLACK;
w->color = RBTREE_RED;
right_rotate(t, w);
w = x->parent->right;
}
// X의 형제 W는 BLACK이고 W의 오른쪽 자식은 RED인 경우
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->right->color = RBTREE_BLACK;
left_rotate(t, x->parent);
x = t->root;
}
}else{
//오른쪽 케이스 ( 왼쪽, 오른쪽만 반대고 동일함)
w = x->parent->left;
if(w->color == RBTREE_RED){
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
right_rotate(t, x->parent);
w = x->parent->left;
}
if(w->right->color == RBTREE_BLACK && w->left->color==RBTREE_BLACK){
w->color = RBTREE_RED;
x = x->parent;
}else{
if(w->left->color == RBTREE_BLACK){
w->right->color = RBTREE_BLACK;
w->color = RBTREE_RED;
left_rotate(t, w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->left->color = RBTREE_BLACK;
right_rotate(t, x->parent);
x = t->root;
}
}
}
x->color = RBTREE_BLACK;
}
free(z);
return 0;
// erase 끝
}참고자료
https://www.youtube.com/watch?v=6drLl777k-E
https://velog.io/@dlwlsh92/WEEK.-02-2022.05.01-TIL
전체코드는
https://github.com/youngcheon/rbtree-lab/blob/main/src/rbtree.c
에서 보실 수 있습니다.

