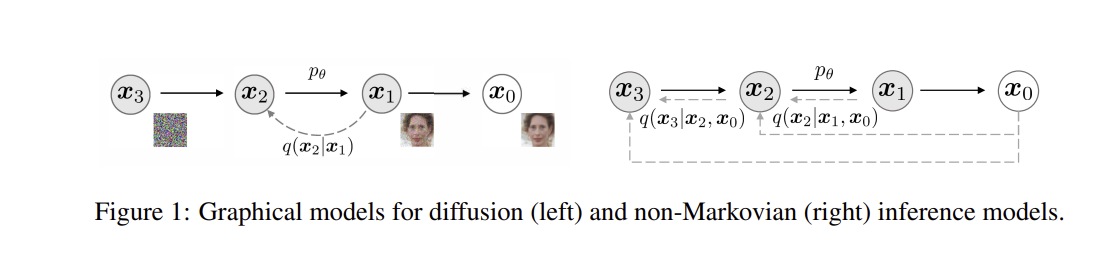
1 Introduction
이미지 생성의 경우, GAN이 VAE, autogressive model ( 자귀회귀모델) , normalizing flows( 정규화 흐름 ) 보다 더 높은 sample을 보인다. 그러나 GAN은 두개의 네트워크 ( Discriminator 와 Generator ) 가 adversarial training을 하여 균형을 이뤄야하고, GAN의 성능은 아키텍청 큰 영향을 받으며, 다양한 샘플을 생성하지 못하는 Mode Collapse 문제가 있다.
최근의 생성모델인 DDPM과 NCSN은 adversairal learning을 하지 않고 GAN에 견줄만한 sample을 생성할 수 있음을 보여주었다. 이를 위해 Gaussian noise 에의해 손상된 sample의 noise의 제거하도록 denoising autoencoding 모델을 train한다. sample은 Markov-chain에 의해 생성되며, Markov-chain 과정은 NCSN에서는 Langevin동역학을 DDPM에서는 foward process를 역으로 수행하며 이루어진다.
DDPM의 generation process는 foward process의 역을 근사하기 때문에 모든 단계를 반복해야 하나의 샘플을 생성할 수 있다는 단점이 있다. 네트워크를 한번 통과하면 되는 GAN과 비교할 때 훨씬 느리다. 예를 들어 같은 GPU를 사용할 때, DDPM으로 50k 32x32 크기 이미지를 샘플링하는데 약 20시간이 걸리지만, GAN으로는 1분이내에 가능하다. 더 큰이미지를 sampling 할 경우, 같은 GPU 에서 50k개의 256x256 크기 이미지를 sampling 하는데 거의 1000시간이 걸릴 수 있다.
DDPM과 GAN 간의 효율성 격차를 해소하기 위해 DDIM을 제안한다. DDPM의 foward process를 non-Markov chain으로 변경한다. 결과적으로 variational training objectives 는 DDPM을 훈련할때 사용했던 식과 일치한다. short generative chain을 사용하여, sampling 속도를 높일 수 있다. 속도가 DDPM에 비해서 훨씬 빠르다.
2 Background
DDIM에 대해서 본격적으로 들어가기전에 DDPM에 나왔던 개념, 수식등을 정리한다
DDPM 의 목표
가 실제 데이터 분포 를 잘 근사하도록 학습하는 것이 목표
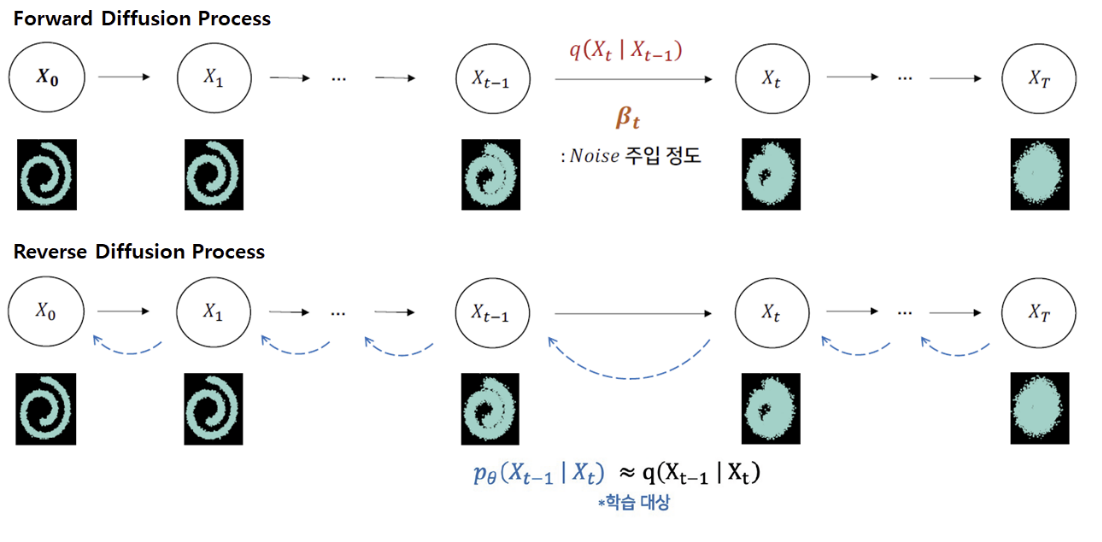
Forward Process
-
forward process ( diffusion process ) 에서는 점진적으로 노이즈를 추가하면서 변형된다. 특정단계에서의 상태 가 에 의존하여 어떻게 분포하는지 나타내며, 이 과정은 Gaussain 분포를 따른다.
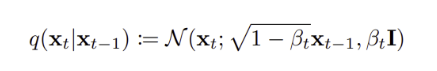
-
Approximate Posterior : 전체 foward process 과정을 나타내며, 로부터 ,, ,,, 모든 latent vector 의 joint distrubution 나타낸다.
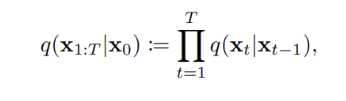
-
특정 시점 t에서의 상태 가 에 조건부로 어떻게 분포되는지?
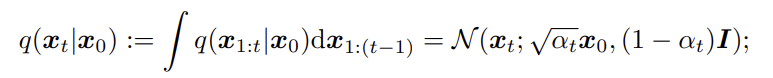 (*DDPM 논문에서는 의 누적곱을 로 표시하지만 DDIM 논문에서는 그냥 로 표시하는 것 같다 )
(*DDPM 논문에서는 의 누적곱을 로 표시하지만 DDIM 논문에서는 그냥 로 표시하는 것 같다 ) -
Reparameterization Trick를 활용하여 다음과 같이 표현할 수 있음
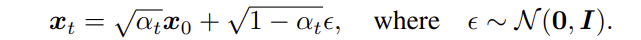
Reverse Process
알고 싶은 것은 이나, 이를 알기는 어려워서 의 parmaeter를 예측 및 학습한다.
- Reverse process :
는 에서 로 가는 조건부 분포를 나타내며, 이는 Gaussain 분포를 따르며, 평균과 공분산은 학습 parameter 에 의해 결정된다.
는 부터 까지의 latent vector의 joint distribution 을 나타낸다.
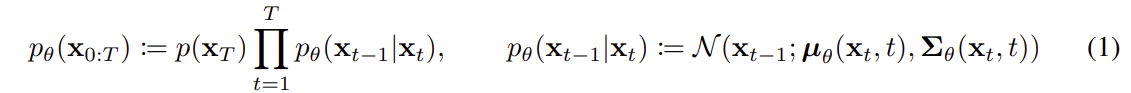
- 는 알 수 없지만, Bayes Rules 에 의해 는 다음과 같이 알 수 있다,

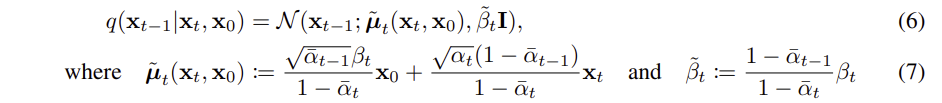
학습 목표
- 를 최대화하는 것이 목표이며, 이를 직접 최대화하는 것이 어려워 ELBO ( 변분 하한 ) 을 활용하여, ELBO를 최대화 하여 이를 근사한다.
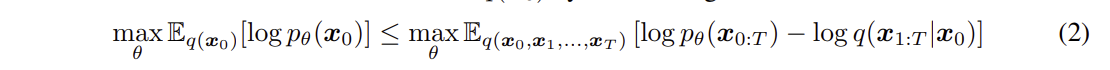
- ELBO를 negative log likelihodd 로 표현하여, 최소화 문제로 변환하였고, 이를 간단히 정리하면 다음과 같다.
최종 Loss 함수라고 생각하면 된다. 예측된 노이즈와 실제 노이즈 간의 차이의 제곱 오차를 최소화하는 것이 목표이다.
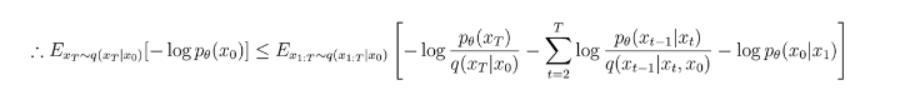
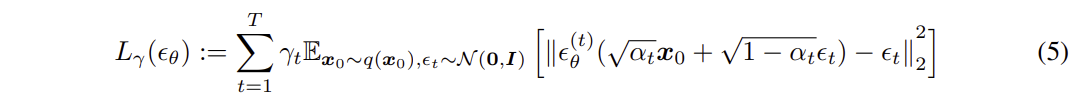
Sampling
노이즈 상태 에서 시작하여 단계별로 노이즈를 제거하면서 최종적으로 를 sampling한다

3 Variational Inference for Non-Markovaion Foward Processes
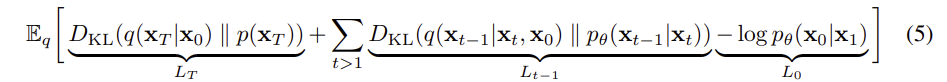
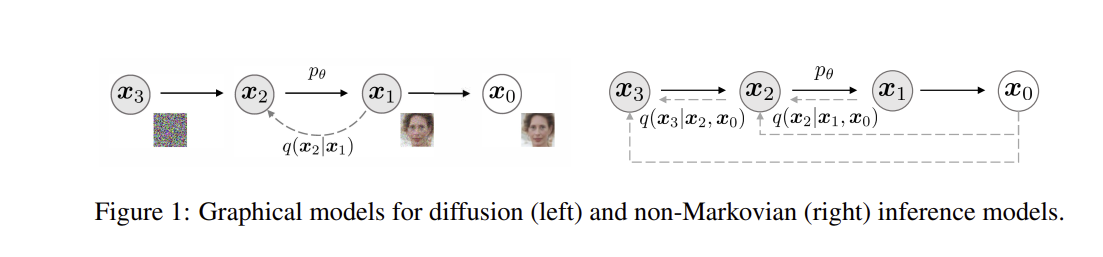
3.1 Non-Markovian Foward Processes
marginal distribution 를 그대로 사용하되,
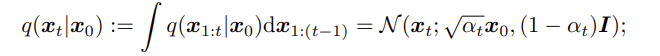
joint distribution을 다음과 같이 바꾼다
- DDPM 에서는 가 바로 이전 step 에 의해 결정되는 markovian chain 이다
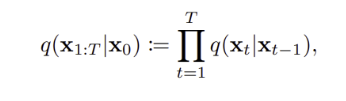
- DDIM 에서는 가 바로 이전 step 과 의해 결정되는 non-markovian chain 으로 바꾼다
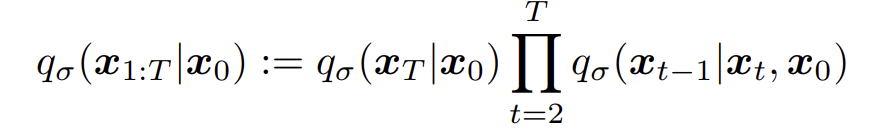
DDPM에 따르면 다음과 같은 식을 만족하고,
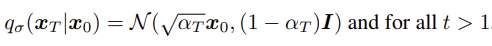 이를 만족하기 위해서는,
이를 만족하기 위해서는,
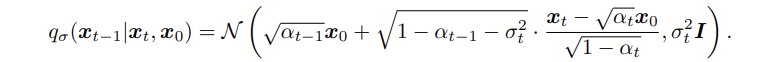
reverse process는 다음과 같이 정리되어야한다.
Forward Process
Foward process는 Bayes Rules에 의해 다음과 같이 표현할 수 있으며, 이는 gaussian distribution을 따른다.
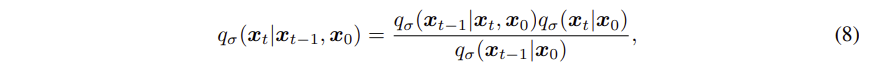
- DDIM의 Forward Process는 non- markovian 이다
- 는 forward process가 얼마나 stochastic 한지를 결정하며, 이 값이 0에 가까워질수록 무작위성이 없어져 와 가 알려진 경우 이 고정된다. 즉, deterministic 해진다
3.2 Generative process and Unified Variational Inference Objective
Generative Process
학습가능한 generative process 를 정의해본다.
각 단계에서 는 를 활용한다.
가 주어지면 를 예측하고, 를 활용하여 를 구한다.
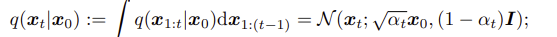
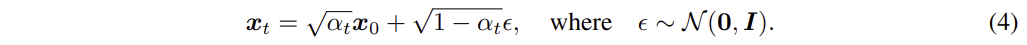 를 활용하여
를 활용하여 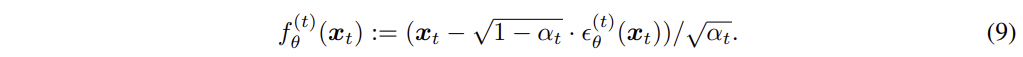 위와 같이 식을 변형할 수 있고, 를 이용하여 을 예측할 수 있다.
위와 같이 식을 변형할 수 있고, 를 이용하여 을 예측할 수 있다.
와 함께, 다음과 같이 정의할 수 있다.
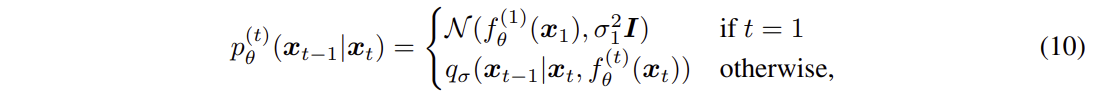
Variational Inference Objective
Generative process 를 최적화 시키기 위해 이용되는 식은 다음과 같고,
이는 DDPM의 ELBO와 같다.

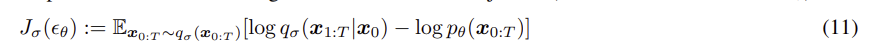
아래 두식을 활용하여 정리하면,
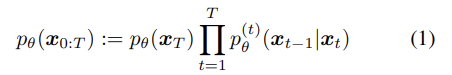
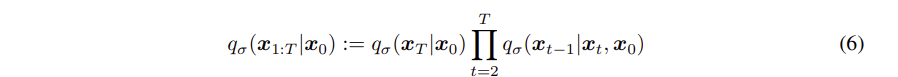
다음과 같은 식이 나온다.
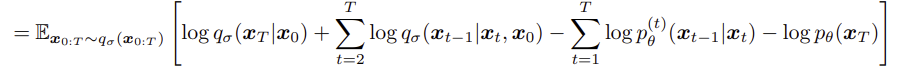
DDIM의 Variational Inference Objective 인 에 대해서
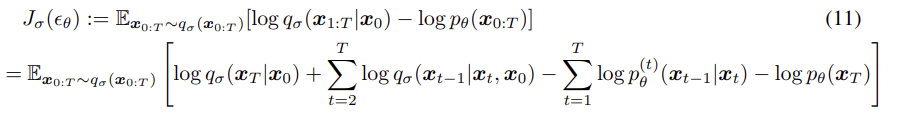
값이 달라질 때마다 다른 Variational Inference Objective 를 가지므로, 이론적으로는 각 σ에 대해 다른 모델을 훈련해야할것 같지만,
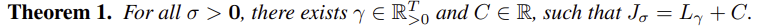 위와 같이 정리1에 따라,
위와 같이 정리1에 따라,
DDPM의 Variational Inference Objective 을 활용하여
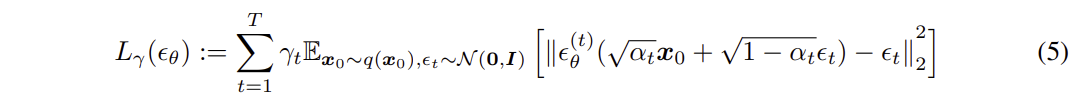
모든 >0 에 대해서 = +C가 존재한다.
- 의 특성으로 인해, 모델의 파라미터가 각 시간 단계 𝑡 마다 공유되지 않는 경우, 가중치 𝛾에 의존하지 않는다는 특성을 가진다
- 의 특성 덕분에, 목표를 사용하여 를 최적화할 수 있다 ( 여기서 인경우는 DDPM의 Variational Inference Objective을 simple하게 한 경우 같음)
4 Sampling From Generalized Generative Processes
4.1 Denoising Diffusion Implicit Models
sampling
위에서 정리한,
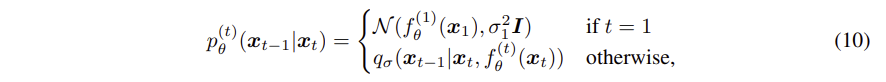
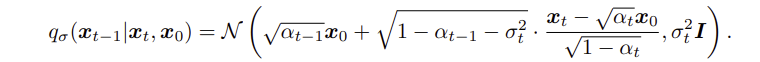
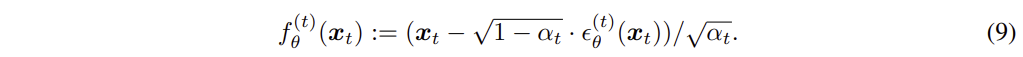
를 활용하여,
x 에 대입하여,
sample 로 부터 를 Sampling 하는 식은 다음과 같다
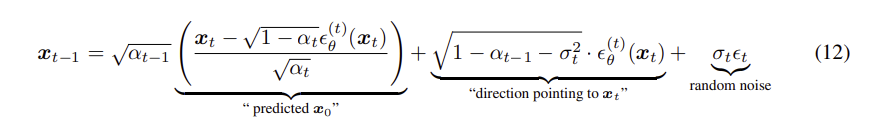
최종적으로 , sampling 하는 과정을 나타내보면
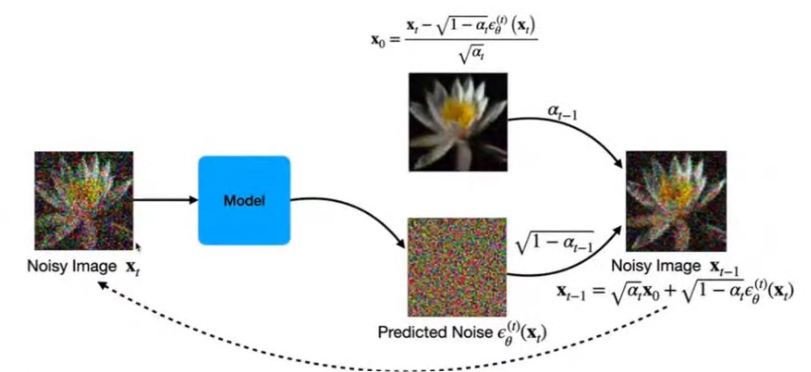
이 그림과 같다.
의 역할
- 는 와 독립적인 gaussian noise이며 = 1로 정의한다
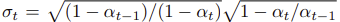 일때, forward pass는 Markov-chain을 이루게 된다. DDPM 방식으로 generate한다.
일때, forward pass는 Markov-chain을 이루게 된다. DDPM 방식으로 generate한다. - = 0이면
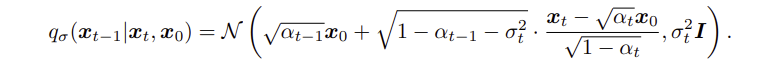
와 같은 식이되고,
random noise의 영향이 없어지기 때문에 implict probabilites model이 된다. 즉, t>=1에 대해 이 와 예측된 가 주어지면 ,deterministic ( stochastic x ) 방식으로 데이터를 생성한다.
-> 즉 , DDPM의 obejctive로 학습된 implicit probabilistic 모델이기 때문에 DDIM(Denoising Diffusion Implicit Model)로 이름 붙였다.
4.2 Accelerated Generation Processes
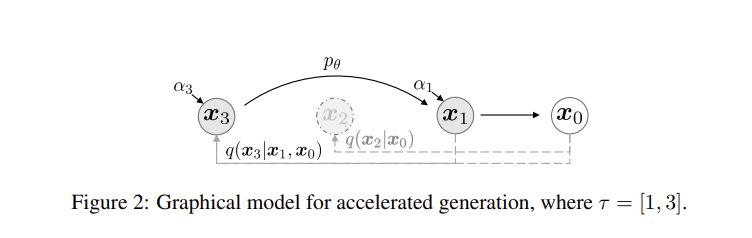
generative process는 reverse process 와 매우 유사하다. 따라서 foward process가 T step을 거친다면 일반적으로 generative process도 T step 을 가져야한다.
가 고정된다면(=0) forward process도 T보다 짧은 step으로 줄일 수 있기 때문에, generative process도 가속화 될 수 있다.
forward pass를 모든 latenet vector 에 대해 정의하는 대신 ,,, , 의 subset에 대해서만 foward 와 generative process 가 진행되어, 계산량이 크게 줄어들게 된다.
또한 t를 continuous time variable로 설정하여, 시간에 따라 변화하는 데이터 분포를 학습할 수 있다. 이는 future work로 남겨둔다.
4.3 Relevance to Neural ODEs
DDIM은 오일러 근사 추정이 가능한 sampling의 형태를 보여준다.
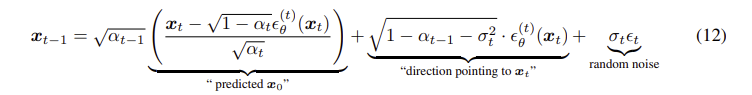
앞서 말했던 것 처럼 = 0 으로 두고, 시간간격을 로 바꿔주면 다음과 같은 식으로 바꿀수 있다.
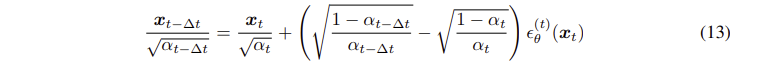
라고 두고, 식을 정리해보면
최종적으로 아래와 같은 식이 나오며 미분방정식이 됨을 확인할 수 있다.
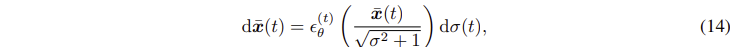
초기조건은 매우 큰 에서 가 정규분포 를 따르고, 충분한 이산화 단계까 있으면 생성과정을 역으로 수행할 수 있다.
DDIM이 SDE가 아니라 ODE를 사용함으로써, 시간 dt가 아니라 라는 변수를 사용하여 데이터를 업데이트 하여, sampling 단계의 수가 적을때 효과적이다.
5 Experimnets
DDIM이 DDPM 보다 이미지 생성에서 더 적은 반복 횟수로 더 나은 성능을 발휘하며, 원래의 DDPM 생성과정에 비해 10배에 100배까지 속도를 높일 수 있다.
DDIM은 가 고정했을 때, 고수준의 이미지 특징을 유지할 수 있어서 latent space에서 interplolation 이 가능하고, latenet vector로 encoding 하고 이 벡터를 사용하여 이미지를 reconsturct 할 수 있다.
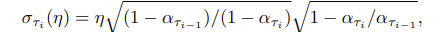
각 데이터셋에 대해서, T=1000, 에서 =1 이고, 와 를 변경해가면서, sample을 생성한다.
5.1 Sample Quality And Efficiency

FID : 생성된 품질을 나타내는 지표 ( 낮을수록 좋음 )
- 샘플을 생성하는데 사용되는 time step 가 증가 할수록 sample의 품질이 높아진다.
DDIM( = 0 ) 인 경우, 작은 time step에서도 높은 샘플 품질을 생성해낸다.
DDPM ( = 1) 인경우, 동일한 time step에서 덜 확률적인 모델에 비해 sample이 일반적으로 나쁘다. ( 여기서 는 DDPM의 보다 큰 값이다 )
- time step 가 동일할때, 다양한 를 적용하여 실험한 결과,
DDPM의 경우 time step 가 작을때 sample 품질이 매우 나쁘다.
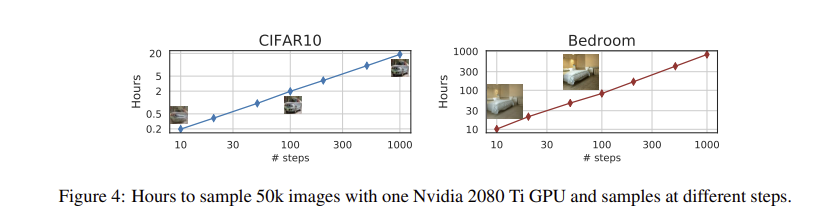
DDIM은 20에서 100스텝 내에 1000스텝 모델과 비교할 수 있는 품질을 생성할 수 있어 이는 DDPM에 비해 10배에서 50배 빠르다. CelebA 데이터셋에서 100스텝 DDPM의 FID 점수는 20 스텝DDIM 과 비슷하다.
5.2 Sample Consistency in DDIMs

DDIM의 경우 generate과정이 deterministic 이여서, 동일한 초기 에서 시작한 경우, 대부분의 high level특징이 유사하다. 20단계로 생성된 샘플이 100단계로 생성된 샘플과 high level면에서 유사하다.
5.3 Interpolation in Deterministic Generative Processes

DDIM은 deterministic 하기 때문에, 단순한 interpolation이 두 샘플 간의 semantic interpolation을 생성할 수 있다.
5.4 Reconstruction from Latenet Space
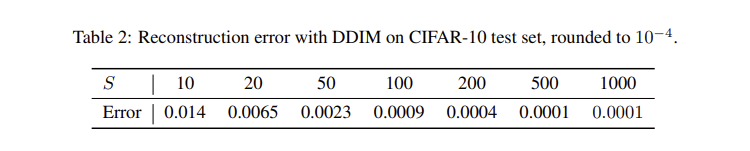
S는 인코딩 및 디코딩 과정에서 사용된 단계로 , S가 증가할 수록 에서 재구성하는 재구성 오차가 줄어든다. 이는 Neural ODE와 유사한 속성을 가지고 있음을 알 수 있다.
( Neral ODE : 시간에 따른 상태 변화를 모델링하여 초기상태에서 최종상태로 연속적으로 변환 )