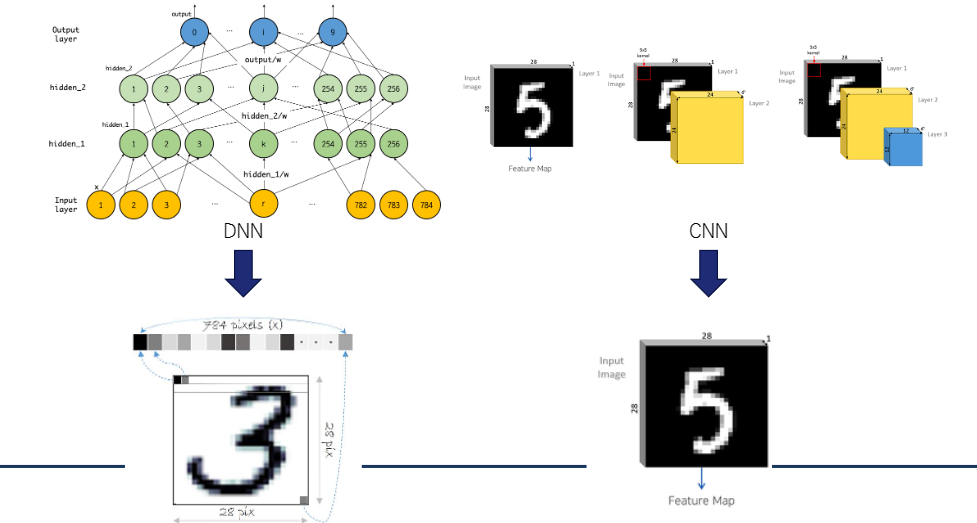
심층 신경망 (DNN)은 다수의 은닉층을 포함하는 인공 신경망을 말한다.
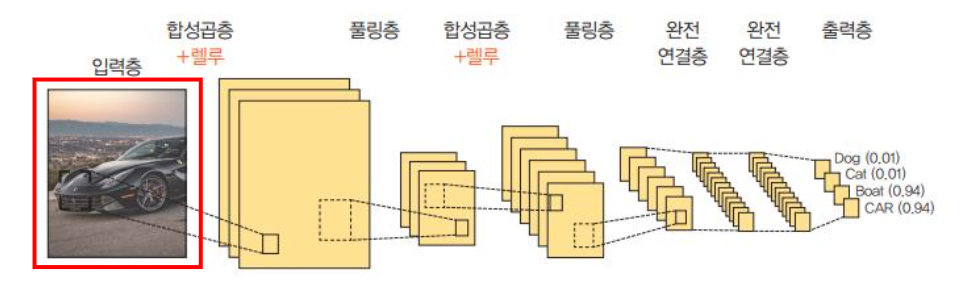
합성곱 신경망(CNN)은 합성곱층(convolutional layer)와 풀링층(pooling layer)를 포함하는 인공 신경망 알고리즘을 뜻한다.
CNN 소개
합성곱층의 필요성
- 데이터의 공간적 구조를 무시하게 된는데...
따라서 이를 방지하기 위해 도입된 것이 합성곱층이다.
입력층
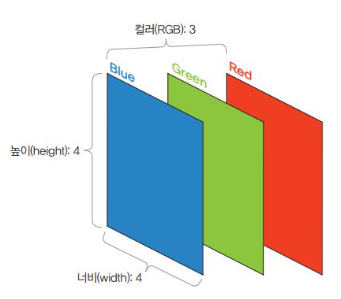
- 입력 이미지 데이터가 최초로 거치게 되는 계층을 말하며 Height x Width x Channel을 뜻
이때, grayscale -> channel 1 ,RGB -> channel3
합성곱층 = 이거 좀 중요해!
- stride : 필터를 적용하는 위치의 간격
- kernel : sliding window 하는 영역에서의 크기
- filter : 실제로 kernel이 weighted sum 하는 영역의 크기
- feature map : 특성 추출된 결과물
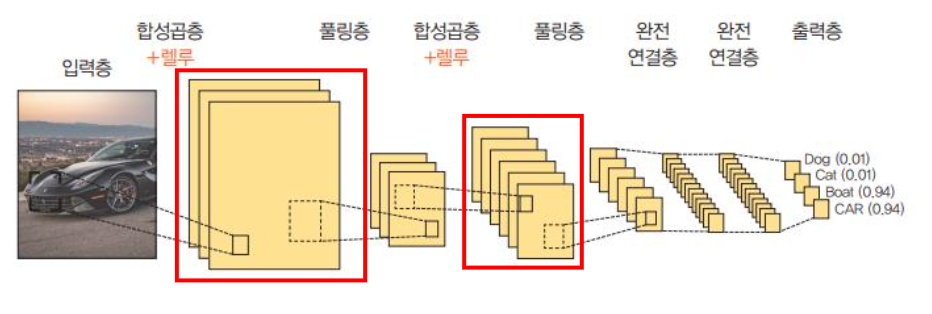
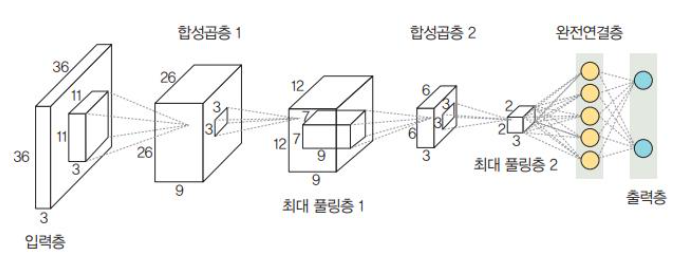
합성곱 신경망 구조
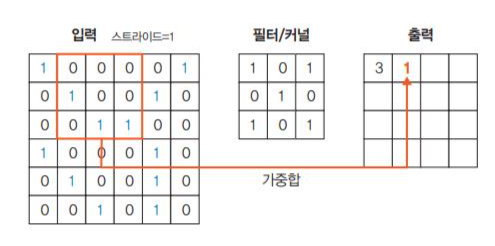
-다음은 스트라이드가 1일때 이동하는 과정을 의미한다.
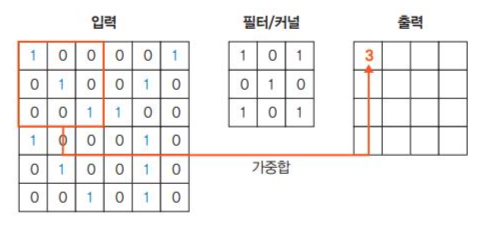
1단계. 입력 이미지에 3x3필터를 적용.
입력 이미지와 필터를 포개 놓고 대응되는 숫자끼리 곱한 후 모두 더한다.
(1x1)+(0x0)+(0x1)+(0x0)+(1x1)+(0x0)+(0x1)+(0x0)+(1x1)=3
2단계. 필터가 1만큼 이동했을 때.
(0x1)+(0x0)+(0x1)+(1x0)+(0x1)+(0x0)+(0x1)+(1x0)+(1x1)=1
.
.
.
.
6단계. 필터가 1만큼 마지막 이동.
(0x1)+(1x0)+(0x1)+(0x0)+(1x1)+(0x0)+(0x1)+(1x0)+(0x1)=1
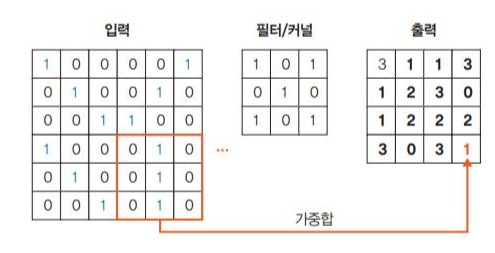
- 앞의 그림에서는 이미지 크기가 (6,6,1)이며, 3x3 크기의 커널 / 필터가 스트라이드 1간격으로 이동하면서 합성곱 연산을 수행하는 것을 보여준다.
- 커널은 스트라이드 간격만큼 순회하면서 모든 입력 값과의 합성곱 연산으로 새로운 특성맵을 만들게 된다.
- 앞의 그림과 같이 커널과 스트라이드의 상호 작용으로 원본 (6,6,1)크기가 (4,4,1)크기의 특성 맵으로 줄어들었다.
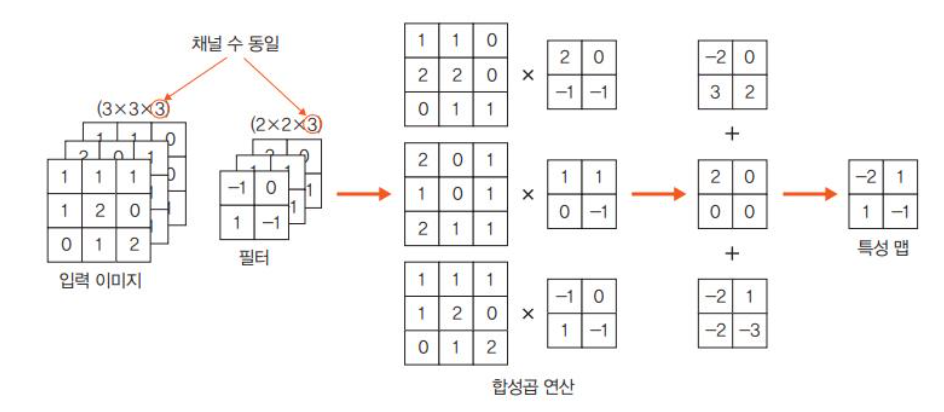
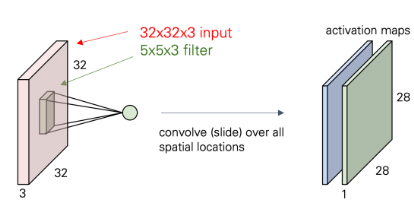
위 사진은 컬러 이미지 합성곱을 의미.
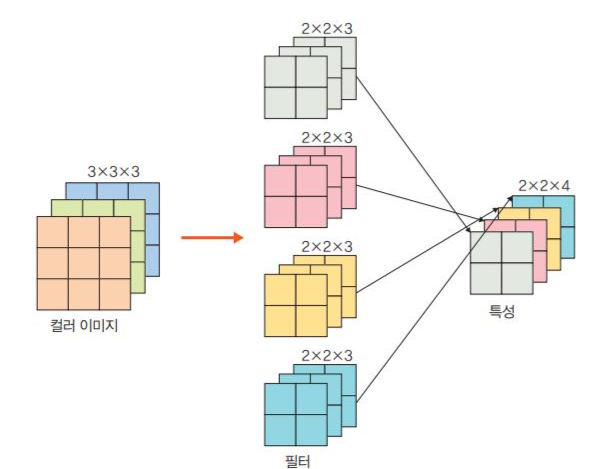
위 사진은 필터가 2이상인 합성곱을 의미.
합성곱 신경망 구조
즉, 합성곱층을 요약하면 다음과 같다.

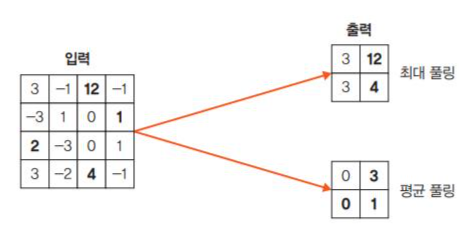
풀링층
은 합성곱층과 유사하게 특성 맵의 차원을 다운 샘플링하여 연산량을 감소하는 것을 말하는데, max pooling은 대상 영역에서 최개밧을 추출하고 average pooling은 대상 영역에서 평균을 반환함을 뜻한다.
완전연결층
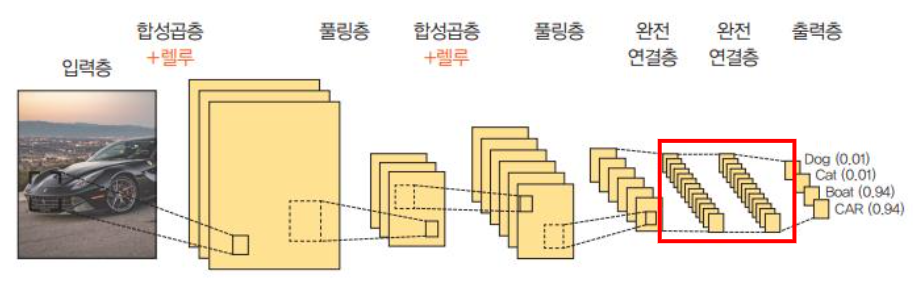
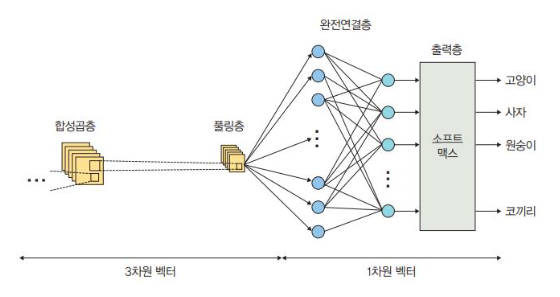
이 과정에서 이미지는 3차원 벡터에서 1차원 벡터로 펼쳐지게 된다.
1D,2D,3D 합성곱
- 합성곱은 이동하는 방향의 수와 출력 형태에 따라 1D,2D,3D로 분류할 수 있다.
1D 합성곱
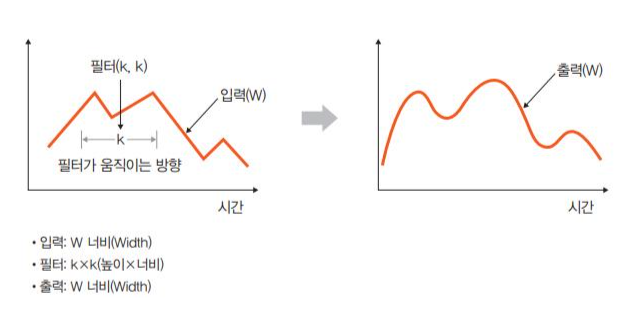
- 1D 합성곱은 필터가 시간을 축으로 좌우로만 이동할 수 있는 합성곱을 말한다.
- 입력(W)와 필터(K)에 대한 출력은 W가 되며 예를 들어 입력이 [1,1,1,1,1]이고 필터가 [0.25,0.5,0.25]라면 ,출력은 [1,1,1,1,1]이 된다.
- 즉, 다음 그림과 같이 출력 형태는 1D의 배열이 되며, 그래프 곡선을 완화할 때 많이 사용한다.
2D 합성곱
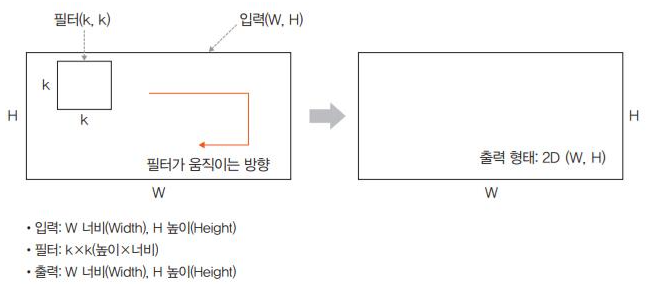
- 2D 합성곱은 필터가 다음 그림과 같이 방향이 두 개로 움직이는 형태를 말한다.
- 즉, 입력(W,H)과 필터(K,K)에 대한 출력은 (W,H)가 되며, 출력 형태는 2D 행렬이 된다.
3D 합성곱
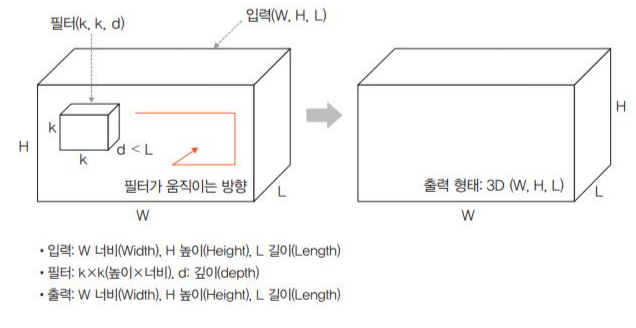
- 3D 합성곱은 필터가 움직이는 방향이 아래 그림과 같이 세 개가 있다.
- 입력(W,H,L)에 대해 필터(k,k,d)를 적용하면 출력으로 (W,H,L)을 갖는 형태가 3D합성곱이다.
- 출력은 3D 형태이먀, 이때 d<L을 유지하는 것이 중요하다.
3D 입력을 갖는 2D 합성곱
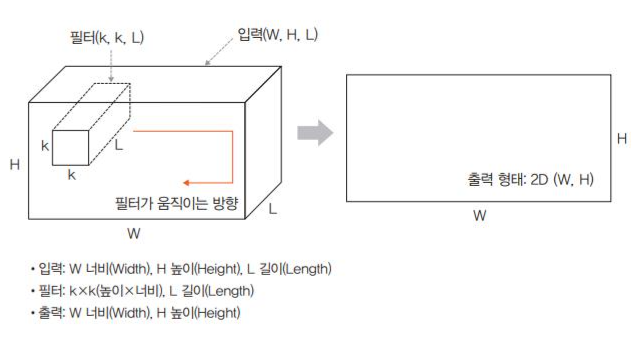
- 입력이(224 X 224 X 3, 112 X 112 X 32)와 같은 3D 형태임에도 출력 형태가 3D 가 아닌 2D 행렬을 취하는 것이 3D 입력을 갖는 2D 합성곱이라 한다.
- 이것은 필터에 대한 길이(L)가 입력 채널의 길이(L)와 같아야 하기 때문에 이와 같은 합성공 형태가 만들어 진다.
- 즉, 입력(W,H,L)에 필터(k,k,L)를 정용하면 출력은 (W,H)가 된다.
- 이때 필터는 다음 그림과 같이 두 방향으로 움직이며 출력 형태는 2D 행렬이 된다.
- 3D 입력을 갖는 2D 합성곱의 대표적 사례로는 LeNet-5와 VGG가 있다.
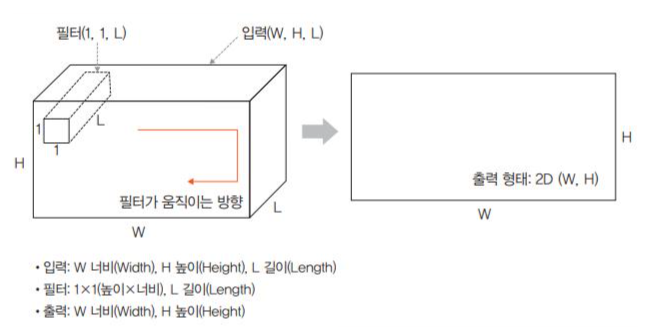
1 x 1 합성곱
- 1x1합성곱은 3D 형태로 입력한다.
- 즉, 입력(W,H,L)에 필터(1,1,L)를 적용하면 출력은 (W,H)가 된다.
- 1 x 1 합성곱체에서 채널 수를 조정해서 연산량이 감소되는 효과가 있으며, 대표적 사례로는 GoogleLeNet가 있다.