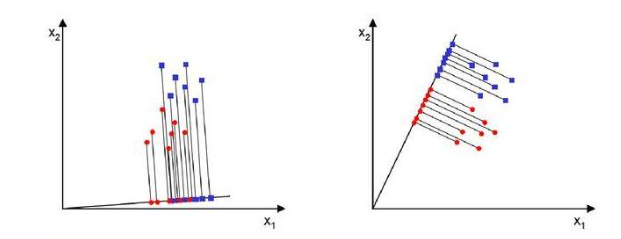
주성분 분석 / PCA
왜 사용할까? -> 주어진 데이터의 간소화를 위해서!
언제 사용하면 좋을까? -> 현재 데이터의 특성(변수)이 너무 많을 경우에는 데이터를 하나의 플롯에 시각화해서 살펴 보는 것이 어렵다. 이때 특성 p개를 두세 개 정도로 압축해서 데이터를 시각화하여 살펴보고 싶을 때 유용한 알고리즘이다.
변수가 많은 고치원 데이터의 경우 중요하지 않은 변수로 처리해야 할 데이터 양이 많아지고 성능 또한 나빠지는 경향이 있다.
이러한 문제를 해결하고자 고차원 데이터를 저차원으로 축소시켜 데이터가 가진 대표 특성만 추출한다면 성능은 좋아지고 작업도 좀 더 간편해질 수가 있다.
차원이란?
차원이란 수학에서는 공간 내에 있느 점등의 위치를 나타내기 위해 필요한 축의 개수를 말한다.
축의 개수=변수의 수=차원 -> 변수의 수가 늘어난다=차원이 늘어난다=데이터 공간이 커진다
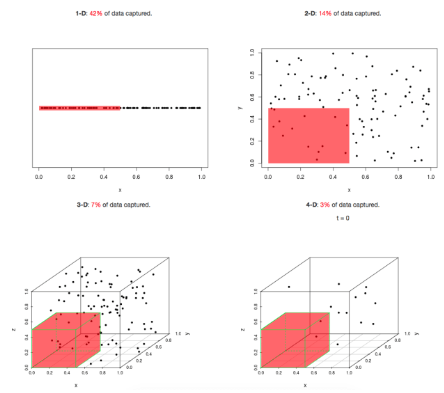
차원의 저주
변수의 수가 많아지면 차원이 커지므로 분석을 위한 최소한의 필요 데이터 건수도 많아진다.
충분한 공간을 표현할 만큼 큰 데이터 수집 없이, 적은 데이터로만 이 공간을 표현하는 경우이다.
Feature Selection
특정 피처에 종속성이 강한 불필요한 피처는 아예 저거하고, 데이터의 특징을 잘 나타내는 주요 피처만 선택하는 것을 말한다.
Feature Extraction
기존 피처를 저차원의 중요 피처로 압축해서 추출하는 것을 말한다.
-새롭게 추출된 중요 특성은 기존 피처가 압축된 것이므로 기존의 피처와는 와전히 다른 값.
단순 암축이 아닌, 피처를 함축적으로 더 잘 설명할 수 있는 또 다른 공간으로 매핑해 추출하는 것을 말한다
->과적합(Overfitting) 영향력이 작아져 원본 데이터의 예측 성능보다 좋은 성능을 보일 수 있다.
주성분 분석 / PCA
여러 변수 간에 존재하는 상관관계를 이용해 이를 대표하는 주성분을 추출해 차원을 축소하는 기법.
-축소할 때 기존 데이터의 유실이 최소화
-가장 높은 분산을 가지는 데이터의 축이 주성분이다.
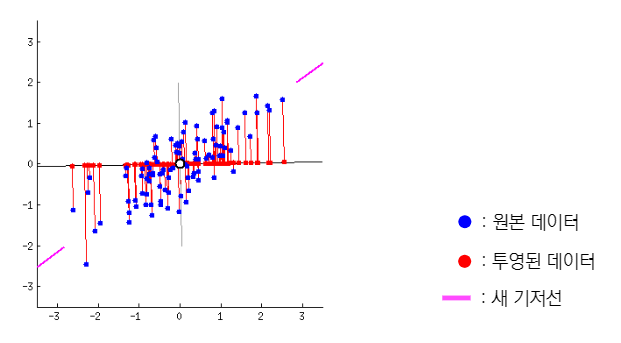
선형대수관점에서의 주성분 분석
입력 데이터의 공분산 행렬을 고유값 분해하고, 고유벡터에 입력 데이터를 선형 변환 하는 것
-> 이때의 고유벡터가 PCA의 주성분 벡터로서 입력 데이터의 분산이 큰 방향을 나타낸다.
선형변환 : 특정 벡터에 행렬 A를 곱해 새로운 벡터를 변환하는 것.
분산 : 데이터의 변동
공분산 : 두 변수 간의 변동
LDA
선형 판별 분석법
PCA와 유사하며 입력 데이터 세트를 저차원 공간에 투영해 차원을 축소하는 기법이다.
지도학습의 분류에서 사용하기 쉽도록 개별 클래스를 분류할 수 있는 기준을 최대한 유지하면서 축소
->클래스 간 분산과 클래스 내부 분산의 비율을 최대화 하는 방식으로 차원을 축소한다.
->클래스 간 분산은 최대한 크게, 클래스 내부의 분산은 최대한 작게.