Duke University: Central Limit Theorem

Sampling distribution

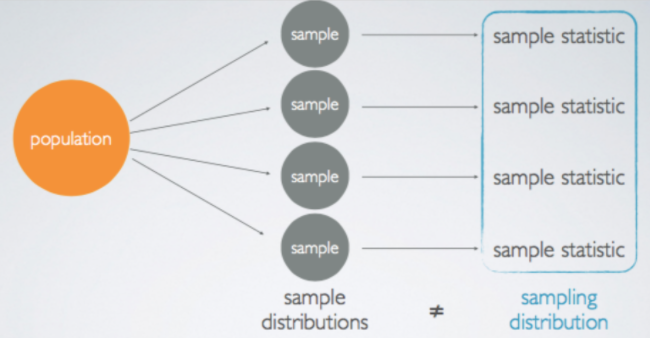
Sampling distribution is the distribution of the means of sample statistics where the samples are taken from a particular population with the same sample size, n.

Standard Error : Standard deviation / Root(n)

• The spread of the sampling distribution, the standard deviation of the sampling distribution of a statistic (the standard deviation of the sample means).
• Typically smaller than the population standard deviation
• if you're running a study, you would only take one sample. So that's the standard deviation of that sample that we would use as our best guess for the population standard deviation

Central Limit Theorem

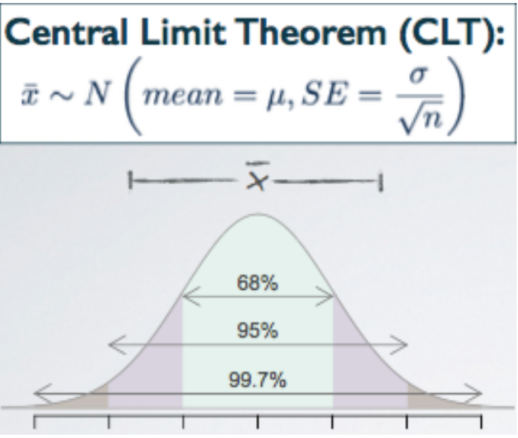
The distribution of sample statistics is nearly normal, centered at the population mean, and with the standard error.

Conditions for CLT

1. Independence: Sampled observations must be independent

   • Random sample (for observational studies) / random assignment (for experimental studies)
   • If sampling without replacement, n < 10% of population
     ※ Suppose you are trying to sample 10 out of 1000 people in a town. If you sample 10 people without replacement, the probability of getting people from the same household is lower than with sample size 100.

2. Sample size/skew:

   • the population distribution is normal
     ※ Larger sample size yields a sampling distribution closer to normal regardless of the population distribution. (rule of thumb: n > 30)
   • A higher sample size would yield a lower standard error.