Duke University : Chi-Square GOF test

Chi-Square GOF test

• Used to evaluate the distribution of one categorical variable with more than 2 levels.
• Evaluating by comparing the distribution of that categorical variable to a hypothetical distribution.
• Used to evaluate if the distribution of levels of a single categorical variable follows a hypothesized distribution.

Evaluating the hypotheses

• quantify how different the observed counts are from the expected counts.
• large deviations from what would be expected based on sampling variation(chance) alone provide strong evidence for the alternative hypotheis.
• called a goodness of fit test since we're evaluating how well the observed data fit the expected distribution.

Conditions for the Chi-square Test

1. Independence: Sampled observations must be independent

• Random sample / assignment
• If sampling without replacement, n < 10% of population
• Each case only contributes to one cell in the table

2. Sample size: Each particular scenario (i.e. cell) must have at least 5 expected counts

Anatomy of a Test Statistic

1. Identifying the difference between a point estimate and an expected value if the null hypothesis were true.
2. Standardizing that difference using the standard error of the point estimate.

Chi-Square Statistic

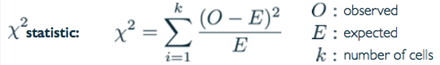
When dealing with counts and investigating how far the observed counts are from the expected counts, we use a new statistic called the chi-square(X2) statistic.

※ A cell is referred to a level of the categorical variable

Why Square?

• Want to get rid of negatives: positive standardized difference
• Not absolute, but square: highly unusual differences between observed and expected will appear even more unusual.

Degrees of Freedom

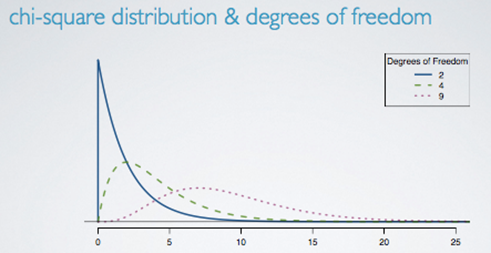
• Chi-square distribution has only one parameter: degrees of freedom: influences the shape, center and spread.
• To determine if the calculated X2 statistic is considered unusually high or not, we need to first describe its distribution.

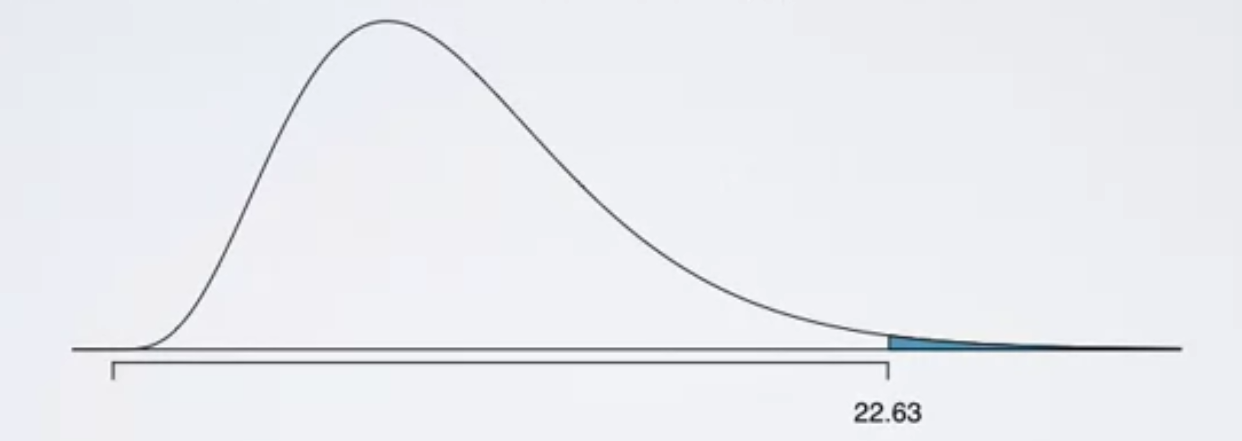
P–value

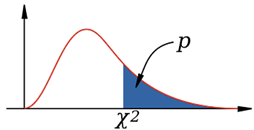
• P-value for a chi-square test is defined as the tail area above the calculated test statistic
• Because the test statistic is always positive, and a higher test statistic means a higher deviation from the null hypothesis
• You get p-value from X2 and d using the table.

INSTRUCTIONS

1. Set the hypothesis

• H0: Actual and expected distributions follow the same distribution
• H1: Actual and expected distributions do not follow the same distribution

2. Calculate the expected number
3. Check conditions
4. Draw sampling distribution, calculate test statistic, shade p-value
5. Make a decision, and interpret it in context of the research question

(example)