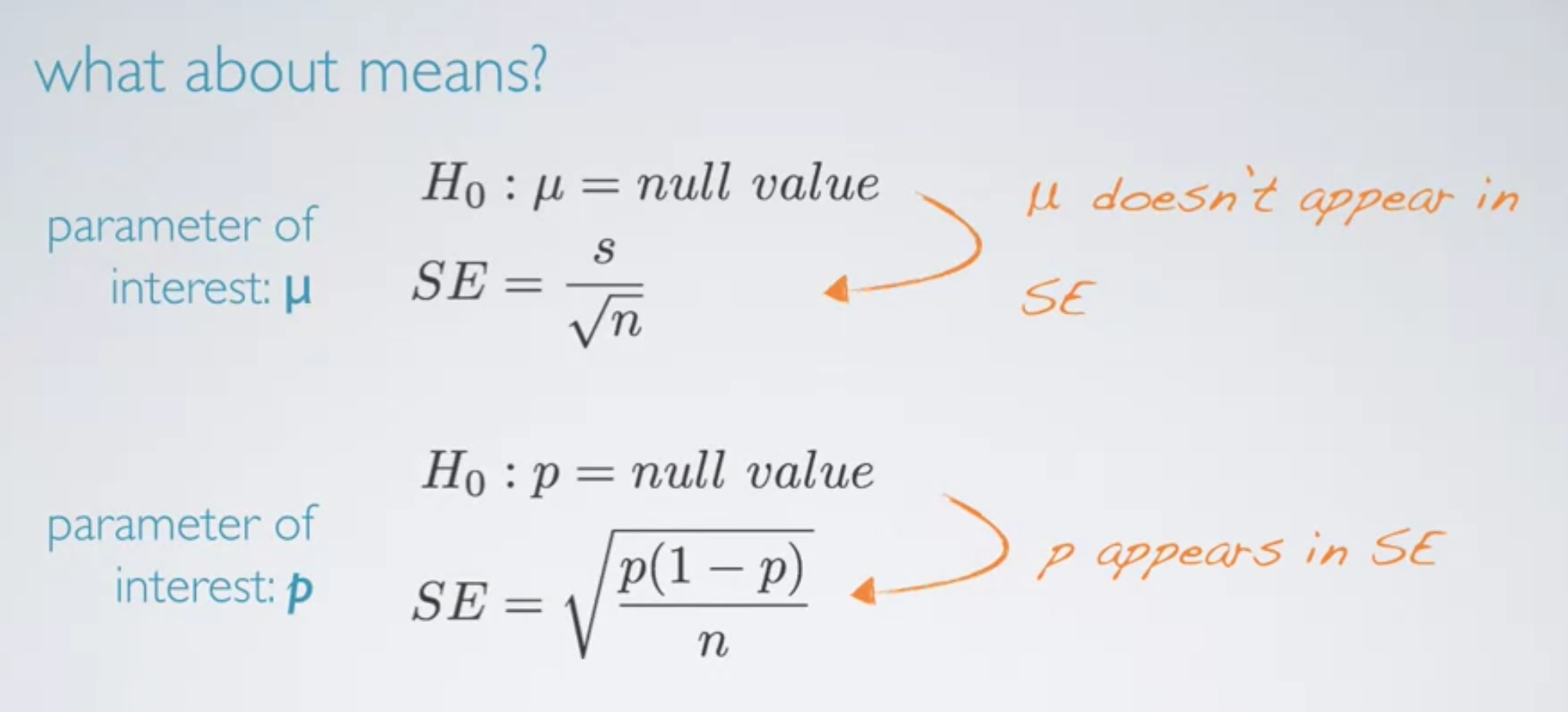Working with One Proportion: p̂ vs p (Review)

- When working with one proportion, we had different formulae for success-failure condition and standard error in both building a confidence interval and conducting a hypothesis test.
Working with Two Proportions

- However, it becomes again different when working with two proportions. We have H0: p1 = p2, but then we wonder what they should be equal to.
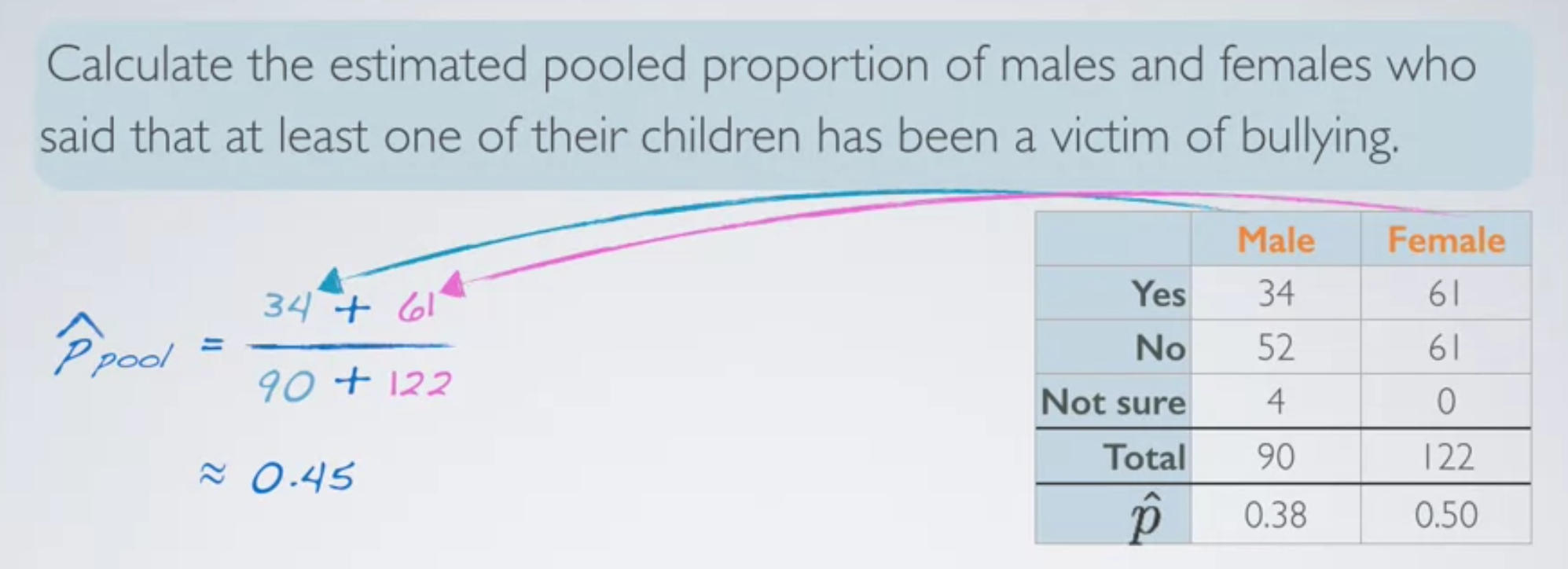
★ Pooled Proportion
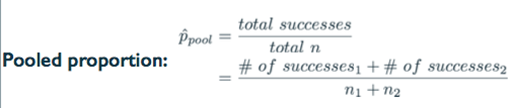
• Calculating the expected successes and failures or the expected proportion for the hypothesis test. For difference between two proportions is not as simple. Take a look at this null hypothesis. We simply say in the null hypothesis that the two population proportions should be equal to each other. Or that their difference should be equal to 0. But at no point do we define what this, these should be equal to. So, we don't have a readily available null value. Of the population proportion that we can use for the two groups to calculate expected successes and expected failures. What do we do? We make one up. This is called the pooled proportion. So the idea here is that even though your null hypothesis does not equate the two population proportions to something. Could we actually come up with a best guess for what these could be equal to under the assumption of the null hypothesis.
When to Use Pooled Proportion
- When conducting a hypothesis test for comparing two proportions
Working with Two Proportions

INSTRUCTIONS
- Calculate the pooled proportion
- Set the hypothesis
- H0 : p1 = p2
- H1 : p1 < or > or != p2
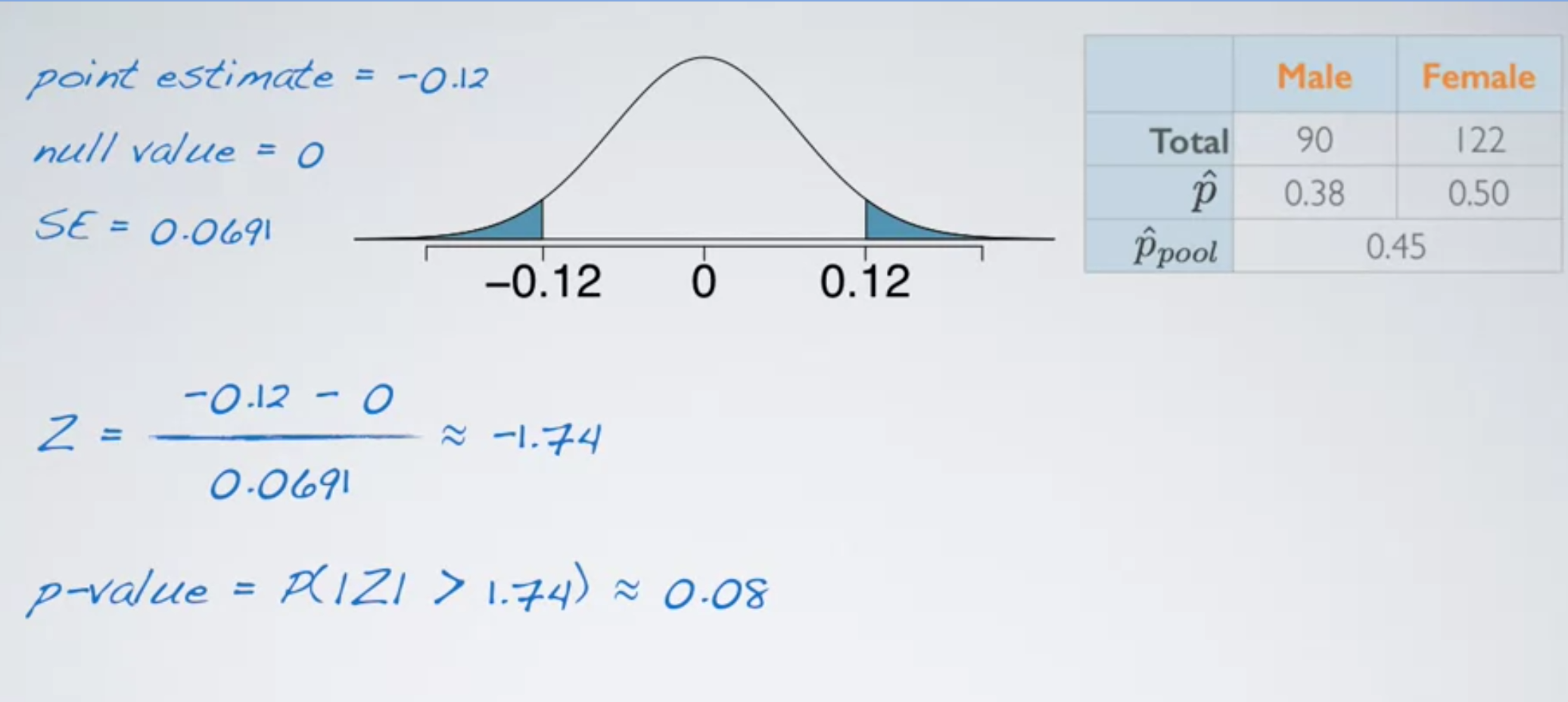
- Calculate the point estimate p̂1 - p̂2
- Check conditions
- Draw sampling distribution, calculate test statistic, shade p-value,
- Make a decision, and interpret it in context of the research question
(example)
※ What about means?