Duke University : Inference for Comparing Two Independent Means

Comparing Two Independent Means

[INSTRUCTIONS]
1. Set the hypothesis

• H0: μx – μy = 0
• H1: μx – μy != 0

2. Check conditions
3. Calculate the point estimate x̄1 - x̄2
4. Draw sampling distribution, calculate test statistic, shade p-value
5. Make a decision, and interpret it in context of the research question:
   See ‘Inference_for_comparing_two_independent_means.pdf’ for an example

★ 2 Steps: Construct a confidence Interval → Conduct a hypothesis test

• Point Estimate
  

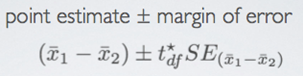
• Standard Error
  
  • This is new. Note that we add the two variances even though we're looking for the standard error of the difference of the two means. This is not simple to prove mathematically with only the tools we've learned in this course so far, but conceptually, you can think about it as bringing together two measures with an inherent variability around them. These are two sample means. When you bring two unknowns together, the result should always be more variable, regardless of whether you're adding them or subtracting them.

• Degrees of Freedom
  
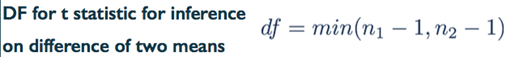
  • You might come across a few other estimates for the degrees of freedom for comparing two means, perhaps in another textbook or so, but what we noted here is actually not the exact degrees of freedom, which is quite tedious to compute by hand. The estimate of degrees of freedom we noted here, is a conservative estimate, since it relies on the lower of the two sample sizes.

1. Set the hypothesis

2. Check Conditions

1) Independence

• Within groups: sampled observations must be independent
  o Random sample / assignment
  o If sample without replacement, n < 10% of population
• Between groups: the two groups must be independent of each other (non-paired)

2) Sample size / skew

• The more skew in the population distributions, the higher the sample size is needed

3. Calculate the point estimate x̄1 - x̄2

4. Draw sampling distribution, calculate test statistic, shade p-value

• Construct a confidence interval by estimating the difference between means

5. Make a decision, and interpret it in context of the research question

• these data provide convincing evidence that there is a difference between the average snack intake of distracted and non-distracted eaters.