Duke University : Sampling Variability and CLT for Categorical Data

Sampling Distribution for Categorical Data

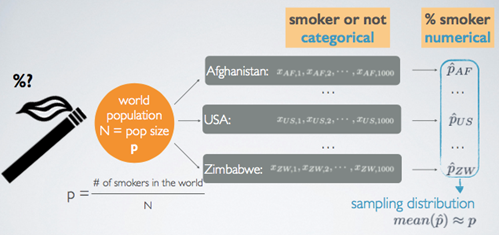
• The sampling distribution is composed of the mean proportions from each sample.

CLT for Proportions

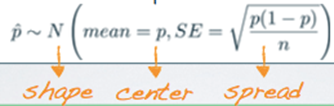
• The sampling distribution of sample proportions is nearly normal, centered at the population proportion, and with a standard error inversely proportional to the sample size.

Conditions for the CLT

1) Independence: Sampled observations must be independent.

• Random sample / assignment
• If sampling without replacement, n < 10% of population

2) Sample size/skew: There should be at least 10 successes and 10 failures in the sample.

• np >= 10 and n(1-p) >= 10

• The same idea of success and failure condition as in the normal approximation of a binomial distribution holds here as the sample proportion needs to be nearly normally distributed.
• When considering the sampling distribution of sample proportions, we don’t have a requirement of n ≥ 30. To determine if the sample size of categorical data is high enough, we instead check the success-failure condition.

(Example)

Since in this case the observation is a sample proportion, standard deviation of that is going to be measured by the standard error, and that gives us a Z score of 2.36.

• You can do the same using the binomial distribution
  

What if the success-failure condition is not met?

• The center of the sampling distribution will still be around the true population proportion
• The spread of the sampling distribution can still be approximated using the same formula for the standard error.
• ★ The shape of the sampling distribution will depend on whether the true population proportion is closer to 0 or closer to 1.

Shape of the Sampling Distribution

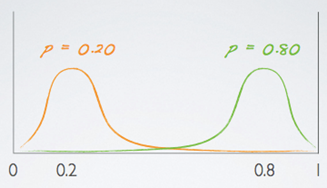
(Back to example)
What would you expect the shape of the sampling distribution of percentages of angiosperms in random samples of 50 plants to look like? (Remember, 90% of all plants species are classified as angiosperms.)
The success-failure condition is not met:
50 x 0.9 = 45 >10 but 50 x 0.1 = 5 < 10

Therefore, the CLT doesn’t apply and the sampling distribution is not nearly normal. Since the true population proportion is close to 1, and the center of the sampling distribution will be at the true population proportion, we expect a shorter tail on the right side and longer tail on the left, yielding a left skewed distribution.