
- Type 1 error is rejecting H0 when you shouldn’t have, and the probability of doing so is alpha (significance level)
- Type 2 error is failing to reject H0 when you should have, and the probability of doing so is Beta
- Power of a test is the probability of correctly rejecting H0, and the probability of doing so is 1 – Beta.
• In a hypothesis test, we obviously want to keep our error rates low, both alpha and beta. However, decreasing one increases the other, and one solution for this problem is getting a larger sample size. Hence, it's important to think about the sample size when designing an experiment. And making sure that resources are invested to recruit a sufficiently large number of subjects to obtain the desired power of the test.
(Example)
Then, according to the central limit theorem, the distribution of the differences in sample means will be nearly normal, with mean 0, because remember, that's what our null value was. And the standard error is the standard error that we calculated, 1.70. Using this information, we can find out what values of the sample statistic we would need to reject the null hypothesis.
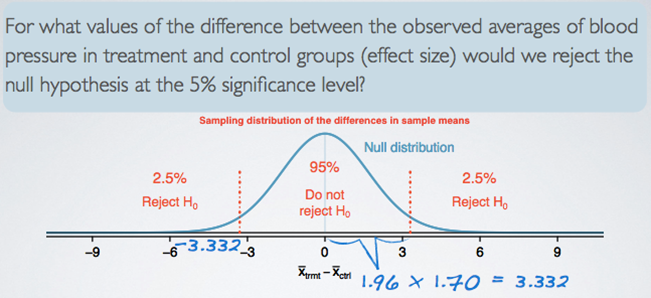
Under the normal model, 95% of the observations fall within 1.96 standard deviations of the mean.
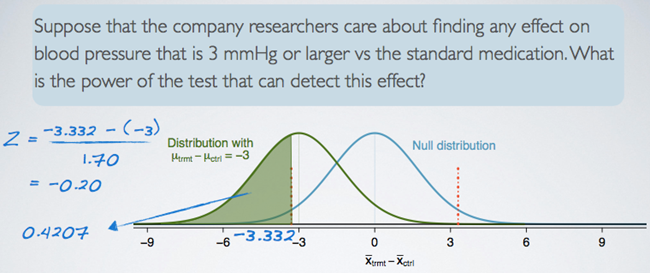
3 millimeters of mercury is the minimum effect size of interest and we want to know how likely we are to detect this size of an effect in this study. If the treatment is indeed effective enough to result in a 3 millimeters of mercury drop in blood pressure on average, then it means the observed distribution of differences in average blood pressures between the two groups will be shifted from the null by 3 millimeters of mercury, as shown in this plot here. We also know that we can only reject the null hypothesis if the observed difference is less than negative 3.332 millimeters of mercury. Putting all of these together, the probability of being able to reject the null hypothesis if the true effect size is negative 3, is equal to the green shaded area under this curve.
The power of the test is 0.4207 when the effect size is negative 3 and each group has a sample size of 100.
It highlights how important it is to not just arbitrarily select a sample size and risk being left with an under powered study. How can we fix things ?
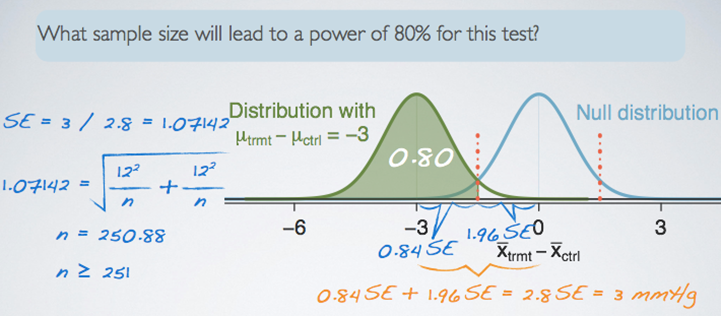
The distance from 0(‘no difference’) to the value of interest(‘-3’) is equal to 3 and in terms of Standard Error it is 2.8SE. We can solve for SE with this equation and finally find out the value of ‘n’ in the SE formula.
The required sample size for 80% of power of the test is at least 251.
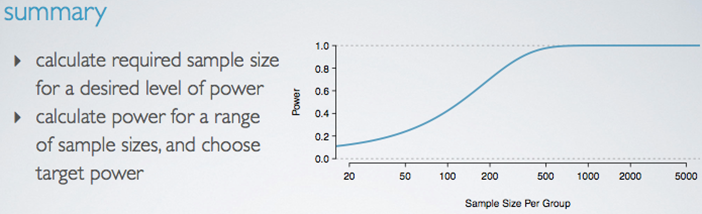
When are these calculations actually used in practice? We can use them when designing a study to calculate a required sample size for a desired level of power. Or we can calculate the power for a range of sample sizes, and choose the target level of the power based on the resources available for collecting the required sample size.
We can see that as the sample size increases so does power but only up to a point, there seems to be no good reason to recruit more than 500 patients or so for each group since the power plateaus at that point. This is important to know when designing a study in order to avoid wasting resources on a sample size that is larger than needed for the maximum power desired.


