Significance vs Confidence Level
The interplay between significance levels used in hypothesis testing as well as confidence levels used in construction of confidence intervals.
So far, we've used two inferential techniques, hypothesis tests and confidence intervals. And it makes sense that the results of these two techniques agree with each other. And they will, if we're using equivalent levels of significance and confidence.
Two-tailed tests
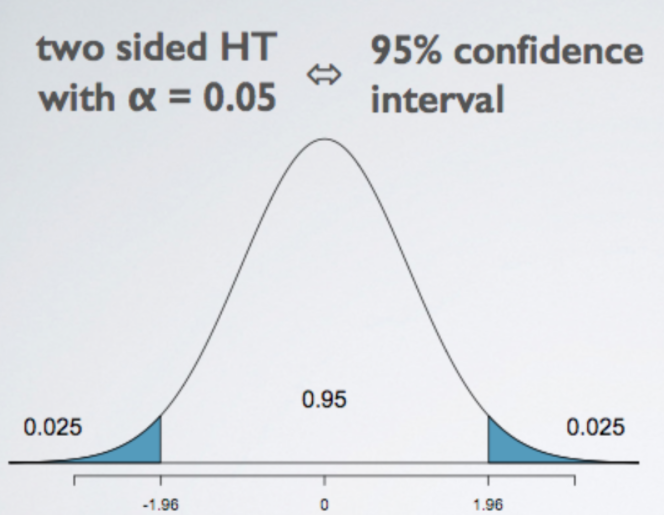
If we add up the 95% in the middle with the alpha on the two tails, we get to the one, which is the entire area under the curve. So indeed, for two-sided hypothesis tests, the significance level and the confidence level are complements of each other.
One-tailed tests
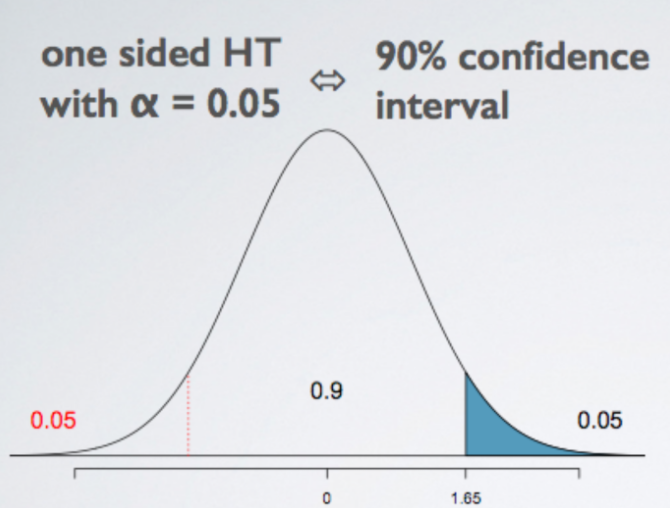
While the lower tail in this figure is of no interest to us within the framework of the hypothesis test. Since confidences always have to be symmetric, and the confidence level is always about the middle whatever percent of the distribution. we can’t have a confidence interval that only goes a certain amount of distance in one direction but more in the other direction, we are actually going to need to think about the 5% in the lower tail, even though we are not going to use it for any sort of decision making within the hypothesis test.
Agreement of CI and HT

