1. 문제 소개
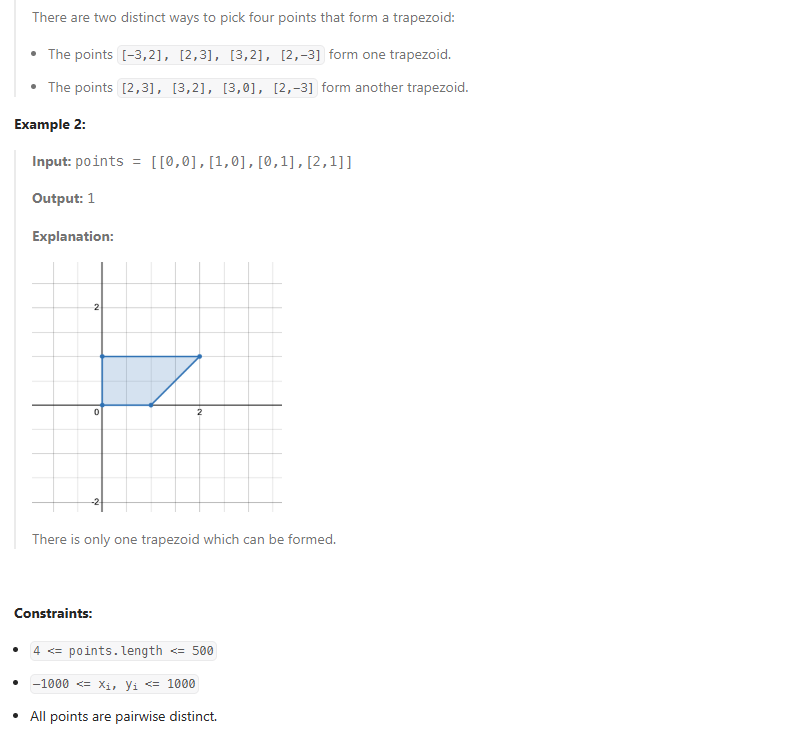
3625. Count Number of Trapezoids II
2. 나의 풀이
어제 풀었던 문제와 거의 비슷한데, 이 풀이는 조금 더 일반적인 풀이에 가깝다.
이번에는 내가 생각했던 풀이가 거의 맞았지만, 사다리꼴을 세다 보니 평행사변형이 중복으로 카운팅이 되었다.
그 부분을 제외하면 거의 맞았었다.
시간복잡도는 이다.
class Solution:
def countTrapezoids(self, points: List[List[int]]) -> int:
MOD = 10**9 + 7 # 결과를 나눌 모듈러 값
n = len(points) # 점의 개수
# 기울기 정규화 함수: 두 점 (x1, y1), (x2, y2)를 잇는 선분의 "표준화된 방향 벡터"를 구한다.
# - dx, dy를 gcd(|dx|, |dy|)로 나누어 기울기를 정규화하고
# - 수직선: (0, 1), 수평선: (1, 0) 으로 고정된 표현을 사용한다.
def slope_form(x1: int, y1: int, x2: int, y2: int):
dx = x1 - x2 # x 좌표 차이
dy = y1 - y2 # y 좌표 차이
if dx < 0: # 방향의 부호를 통일하기 위해 dx를 항상 0 이상으로 맞춘다.
dx = -dx
dy = -dy
if dx == 0: # 수직선: dx = 0 → 기울기 '무한대'를 (0, 1)로 표현
return (0, 1) # vertical
if dy == 0: # 수평선: dy = 0 → 기울기 0을 (1, 0)으로 표현
return (1, 0) # horizontal
g = gcd(abs(dx), abs(dy)) # dx, dy의 최대공약수
dx //= g # dx, dy를 gcd로 나누어 기울기를 기약 비율로 정규화
dy //= g
return (dx, dy) # 정규화된 방향 벡터(기울기 표현) 반환
# mp[slope][intercept] = 해당 slope와 intercept를 갖는 "직선 위의 선분 개수"
# - slope: 정규화된 (dx, dy)
# - intercept: 같은 slope에서 직선을 분리하는 ID 역할 (dy * x - dx * y 형태)
mp = defaultdict(lambda: defaultdict(int))
# 대각선의 중점 기준으로 평행사변형을 카운트하기 위해 사용하는 자료구조들
mids = defaultdict(int) # mids[(mx, my)] = 해당 중점을 갖는 "모든 대각선의 수"
mids_diff = defaultdict(lambda: defaultdict(int))
# mids_diff[(mx, my)][slope] = 해당 중점과 해당 slope를 갖는 대각선의 수
pgram = 0 # 평행사변형 개수(나중에 ans에서 빼줄 값)
# 1. 모든 점쌍을 순회하며:
# - 기울기와 직선 ID(intercept)를 계산해 mp에 선분 개수 누적
# - 동시에 두 점을 "대각선 후보"로 보고, 중점 + 기울기 정보로 평행사변형 개수를 센다.
for i in range(n):
x1, y1 = points[i]
for j in range(i + 1, n):
x2, y2 = points[j]
# (i, j)를 잇는 선분의 정규화된 기울기(방향 벡터)
s = slope_form(x1, y1, x2, y2)
dx, dy = s
# 같은 기울기를 가진 직선을 dy * x - dx * y = c 꼴로 표현
# - (dx, dy)가 동일하고 c가 같다면 동일한 직선 위에 있음
intercept = dy * x1 - dx * y1
mp[s][intercept] += 1 # 해당 직선 위의 선분 개수 +1
# (x1, y1), (x2, y2)를 "대각선"으로 보고,
# 중점 (mx/2, my/2)를 나타내는 정수 key (mx, my) = (x1 + x2, y1 + y2)를 사용
mx = x1 + x2 # 실제 중점의 x좌표는 mx / 2 이지만, 비교용으로 합만 사용
my = y1 + y2 # 실제 중점의 y좌표는 my / 2
# 같은 중점을 가지는 모든 대각선 쌍은 "평행사변형"을 만들 수 있는 후보이다.
# 그중에서도 서로 다른 기울기의 대각선 쌍만 평행사변형을 만든다.
#
# mids[(mx, my)] : 지금까지 같은 중점을 가진 모든 대각선의 수
# mids_diff[(mx, my)][s] : 그 중, slope = s 인 대각선의 수
#
# 현재 대각선(s, (mx, my))가 추가되기 전에,
# - 같은 중점 (mx, my)를 가진 기존 대각선은 mids[(mx, my)] 개
# - 그 중 기울기 s를 가진 것은 mids_diff[(mx, my)][s] 개이므로
# - "기울기가 다른" 대각선은 mids[(mx, my)] - mids_diff[(mx, my)][s] 개
# 이 각각과 현재 대각선을 짝지으면 평행사변형 1개씩 생성.
pgram += mids[(mx, my)] - mids_diff[(mx, my)][s]
# 상태 업데이트: 현재 대각선을 중점/기울기 카운트에 반영
mids[(mx, my)] += 1
mids_diff[(mx, my)][s] += 1
# 2. slope별로 "평행한 두 직선 쌍"을 이용해 만들 수 있는 사다리꼴/평행사변형 개수 카운트
# - mp[slope][intercept] = 해당 직선 위 선분 개수
# - 같은 slope 안에서, 서로 다른 intercept를 갖는 두 직선을 선택하고,
# 각 직선에서 선분을 하나씩 고르는 모든 조합 수를 합산한다.
ans = 0
for slope, vals in mp.items():
tot = 0 # 현재 slope에서 이전까지 처리한 모든 직선의 선분 개수 총합
for cnt in vals.values(): # cnt: 특정 intercept 직선 위의 선분 개수
# 서로 다른 두 직선을 선택해, 각 직선에서 선분을 하나씩 선택하는 조합:
# - 이전까지 존재한 선분 수 tot 와 현재 직선의 선분 수 cnt 의 곱
ans = (ans + cnt * tot) % MOD
tot += cnt # 누적 선분 개수 업데이트
# 3. 평행사변형 제거(중복 카운트 보정)
# - 위 ans에는 일반 사다리꼴 + 평행사변형이 모두 포함되어 있고,
# 특히 평행사변형은 "두 가지 기울기(s1, s2)"에서 각각 한 번씩 중복 카운트된다.
# - pgram은 "서로 다른 기울기의 대각선 쌍"을 이용해 세어낸 평행사변형 개수이다.
# - 따라서 최종 정답은 ans - pgram.
ans = (ans - pgram) % MOD
return ans # 중복이 보정된 최종 사다리꼴 개수 반환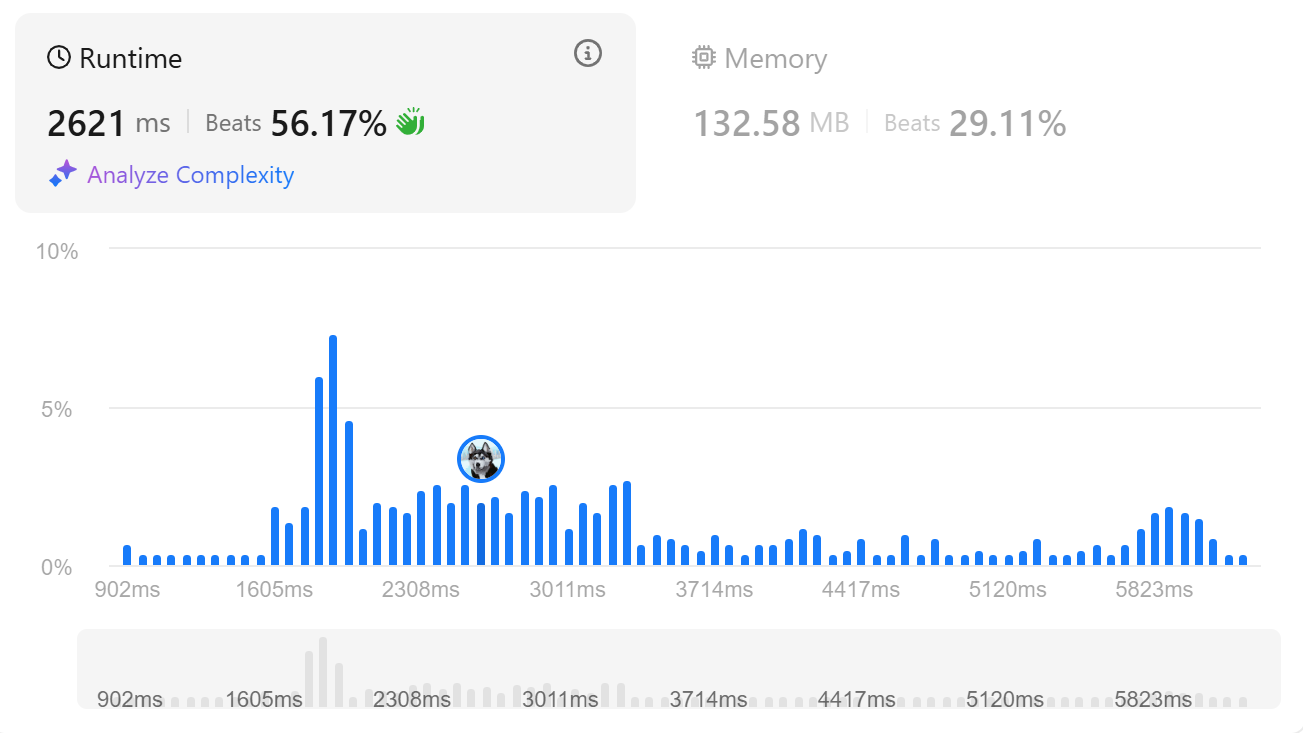
3. 다른 풀이
Editorial의 풀이는 다음과 같았다.
똑같이 시간복잡도는 이다.
class Solution:
def countTrapezoids(self, points: List[List[int]]) -> int:
n = len(points) # 점 개수
inf = 10**9 + 7 # 수직선의 '기울기'를 표현하기 위한 특수 값(무한대 기울기 역할)
slope_to_intercept = defaultdict(list) # (기울기 k) -> 해당 기울기를 가지는 모든 직선의 절편 b 리스트
mid_to_slope = defaultdict(list) # (대각선 중점 key) -> 그 대각선의 기울기 k 리스트
ans = 0 # 사다리꼴(및 평행사변형) 개수를 누적할 변수
# 모든 점 쌍 (i, j)를 순회하며:
# - 두 점을 지나는 직선의 기울기 k, 절편 b를 계산
# - 두 점의 중점(대각선 관점)을 나타내는 key를 계산
for i in range(n):
x1, y1 = points[i]
for j in range(i + 1, n):
x2, y2 = points[j]
dx = x1 - x2 # x 좌표 차이
dy = y1 - y2 # y 좌표 차이
# 1) 직선의 기울기 k, 절편 b 계산
if x2 == x1:
# 수직선의 경우: 기울기는 '무한대' 취급, b에는 x절편(= x좌표)을 저장
k = inf
b = x1
else:
# 기울기 k = (y2 - y1) / (x2 - x1)
k = (y2 - y1) / (x2 - x1)
# y = kx + c 형태에서 c를 구하는 대신, 수식 변형으로 절편 b를 계산
# b = (y1 * dx - x1 * dy) / dx 는 기하적으로 동일한 직선이면 같은 b를 갖도록 하는 표현
b = (y1 * dx - x1 * dy) / dx
# 2) 두 점의 "대각선 중점"을 나타내는 key 계산
# - 실제 중점은 ((x1 + x2)/2, (y1 + y2)/2)이지만,
# 비교만 하면 되므로 (x1 + x2, y1 + y2)를 사용하고,
# x쪽에 10000을 곱해 한 정수로 묶는다.
mid = (x1 + x2) * 10000 + (y1 + y2)
# 같은 기울기 k를 갖는 직선들의 절편 b를 저장 (나중에 평행 직선 쌍 카운트용)
slope_to_intercept[k].append(b)
# 같은 중점 mid를 갖는 대각선들의 기울기 k를 저장 (나중에 평행사변형 카운트용)
mid_to_slope[mid].append(k)
# -------------------------------------------------
# 1단계: slope_to_intercept를 이용해
# - "평행한 두 직선 쌍"을 이용해 만들 수 있는 사다리꼴/평행사변형의 총 개수를 센다.
# - 여기서는 '기울기 k가 같은 직선들'을 모으고, '서로 다른 절편 b를 가진 직선 쌍'의 개수를 세는 구조.
# -------------------------------------------------
for sti in slope_to_intercept.values():
if len(sti) == 1: # 해당 기울기를 가지는 직선이 1개뿐이면 쌍을 만들 수 없음
continue
cnt = defaultdict(int) # 같은 절편 b를 가진 직선 개수를 세기 위한 카운터
for b_val in sti:
cnt[b_val] += 1 # 절편 b값별로 직선 개수 증가
total_sum = 0
# cnt.values(): 각 절편 b마다 그 절편을 갖는 직선 개수
# 서로 다른 절편 b1, b2를 갖는 직선들 중에서 '직선 한 개씩'을 고르는 모든 쌍을 세기 위해
# 누적 합 방식으로 조합수를 계산한다.
for count in cnt.values():
# 현재 절편 그룹의 직선 개수 = count
# 이전까지 등장한 직선 개수의 합 = total_sum
# -> 서로 다른 절편 그룹 사이 조합: count * total_sum
ans += total_sum * count
total_sum += count # 누적 직선 개수 업데이트
# 이 시점에서 ans에는
# - "한 기울기 k에 대해 서로 다른 두 직선 쌍을 고를 수 있는 경우의 수"가 모두 합쳐져 있다.
# 즉, '평행한 두 변을 기준으로 정의한 사각형(사다리꼴 + 평행사변형)' 개수를 세어 놓은 상태이다.
# 문제는 평행사변형이 '두 가지 기울기(k1, k2)'에서 중복으로 세어진다는 점이다.
# -> 평행사변형 개수를 한 번 빼주어야 "서로 다른 사다리꼴 개수"가 된다.
# -------------------------------------------------
# 2단계: mid_to_slope를 이용해
# - 평행사변형 개수를 구해서 ans에서 빼준다.
# - 평행사변형의 성질:
# · 두 대각선의 중점이 같다.
# · 두 대각선의 기울기가 (기울기 상 서로 다른 직선 쌍)을 갖는다.
# - 같은 mid(중점)를 갖는 점쌍(대각선 후보)들 중에서
# 서로 다른 두 대각선을 고를 때,
# 각 대각선의 기울기를 고려해 중복을 제거하는 구조이다.
# -------------------------------------------------
for mts in mid_to_slope.values():
if len(mts) == 1: # 해당 중점을 갖는 대각선이 1개뿐이면 평행사변형 불가
continue
cnt = defaultdict(int) # 같은 기울기 k를 갖는 대각선 개수 카운트
for k_val in mts:
cnt[k_val] += 1 # 기울기별로 대각선 개수 증가
total_sum = 0
# 여기서도 마찬가지로,
# - 서로 다른 기울기의 대각선 쌍을 고르는 경우의 수를 세기 위해
# - 누적 합(total_sum)을 사용해 count * total_sum을 더한다.
# 이렇게 얻어지는 값은:
# - "해당 중점을 공유하는 서로 다른 기울기의 대각선 쌍" 개수
# - 즉, 이 중점에서 만들어지는 평행사변형 개수에 해당한다.
for count in cnt.values():
ans -= total_sum * count # 평행사변형만큼 ans에서 빼서 중복 카운트를 보정
total_sum += count # 기울기별 대각선 개수 누적
return ans # 최종적으로 중복 보정이 끝난 사다리꼴 개수 반환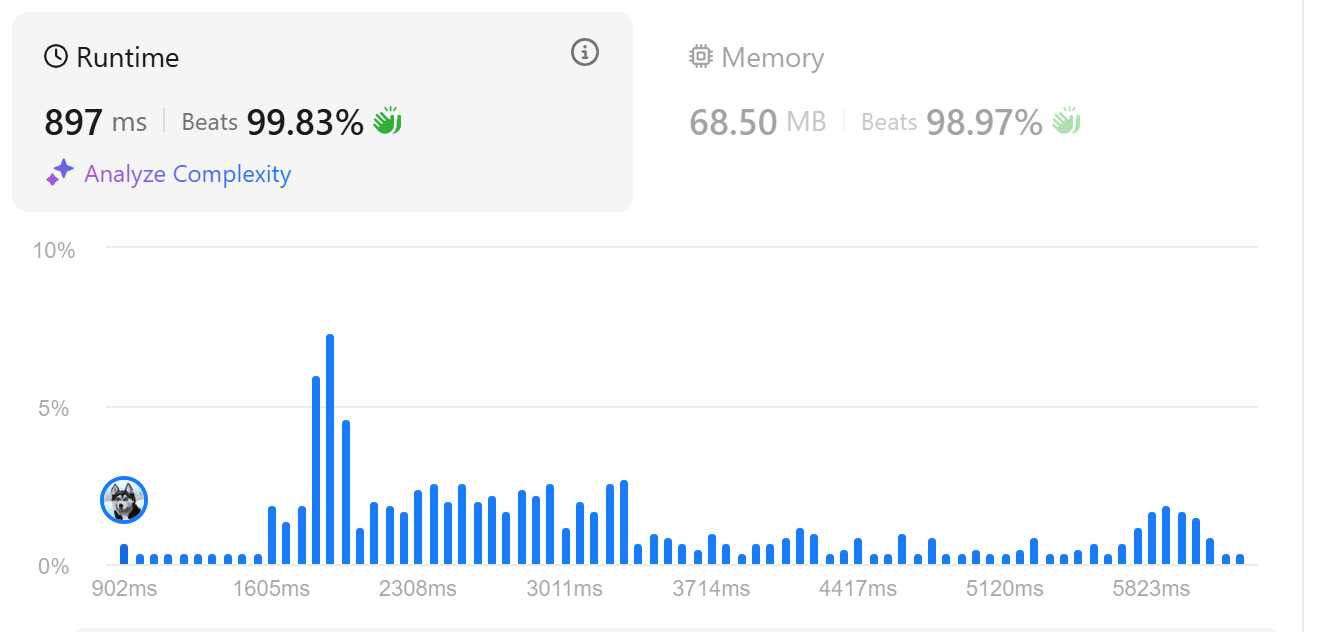
4. 마무리
이번에도 내 힘으로 끝까지 풀지는 못해 너무 아쉽다.
계속 노력해야겠다.
