1. 문제 소개

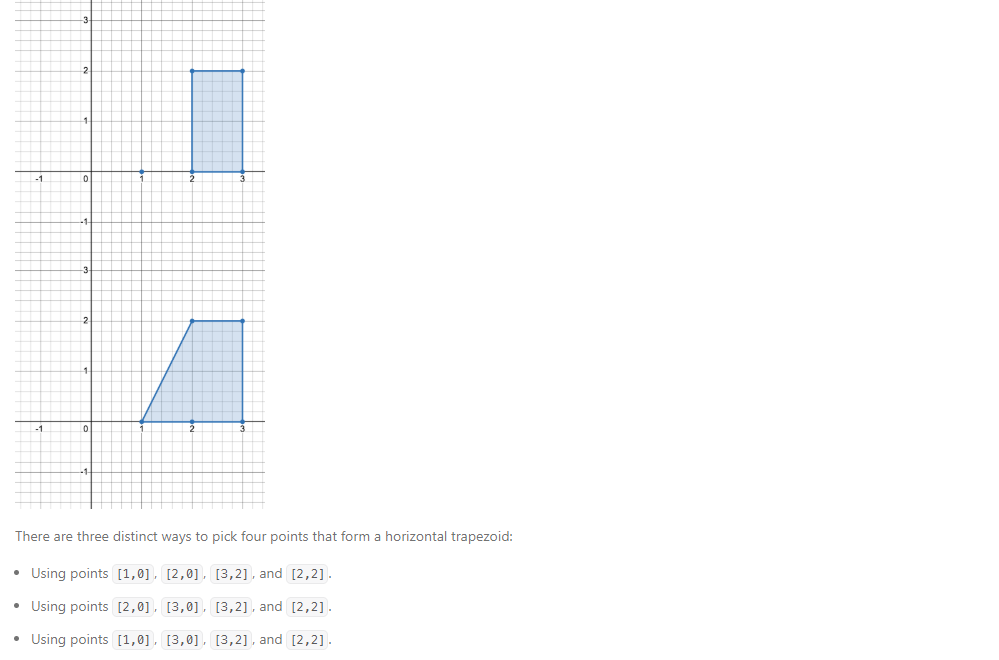
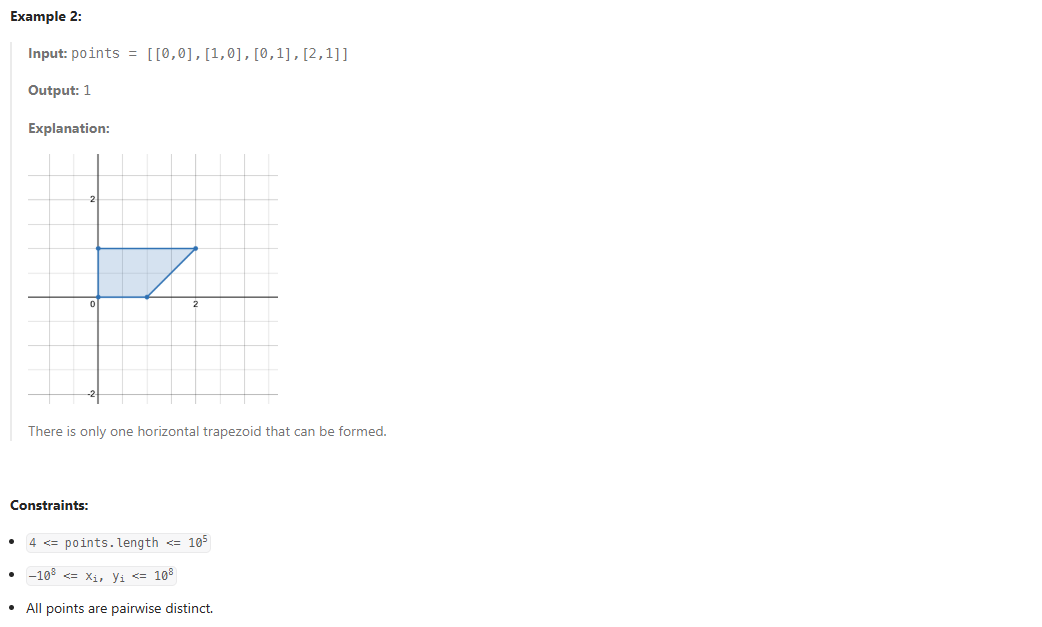
3623. Count Number of Trapezoids I

2. 나의 풀이

오늘부터는 조금 오래 걸리더라도 직접 풀어보고 안 되면 다른 풀이를 보기로 했다.
처음에는 기울기에 맞춰서 점들을 모아 4개의 점이 겹치지 않는 경우를 세었다.
그러나 시간복잡도가 너무 커져서 실패하고 말았다.
사실 이 풀이의 경우는 x축과 평행한 사다리꼴만 계산하면 되기도 했다.
결국 editorial의 풀이를 적용했다.
시간복잡도는 $O(n)$이다.

class Solution:
    def countTrapezoids(self, points: List[List[int]]) -> int:
        point_num = defaultdict(int)          # 각 y좌표별로 점의 개수를 세기 위한 딕셔너리
        MOD = 10**9 + 7                       # 문제에서 요구하는 모듈러 연산
        ans, total_sum = 0, 0                 # ans: 최종 사다리꼴 수, total_sum: 누적 수평선 수

        for point in points:
            point_num[point[1]] += 1          # 같은 y값을 가진 점의 개수를 카운트

        for p_num in point_num.values():
            edge = p_num * (p_num - 1) // 2   # 해당 y층에서 만들 수 있는 수평선 개수 = 조합 C(p_num, 2)
            ans = (ans + edge * total_sum) % MOD  
            # 현재 y층에서 생성된 수평선(edge) × 이전 y층까지 누적된 수평선(total_sum)
            # → 두 층을 묶어 만들 수 있는 모든 사다리꼴 수를 더함

            total_sum = (total_sum + edge) % MOD  
            # 현재 층의 수평선을 누적하여 다음 층 계산에 사용

        return ans                            # 최종 사다리꼴 수 반환

3. 다른 풀이

같은 y좌표에 있는 점 f개는 만들 수 있는 수평선 수는 z = C(f, 2) = f(f−1)/2 이다.
서로 다른 y층 i, j 에 대해 만들 수 있는 사다리꼴 수는 zᵢ · zⱼ 이므로, 모든 i<j 쌍의 합을 구해야 한다.
이를 직접 이중 반복문으로 계산하면 O(k²)이지만, (Σz)² − Σ(z²) = 2·Σ(zᵢzⱼ) 를 이용하면 전체를 한 번의 선형 반복(O(k))으로 계산 가능하다.
좌표 개수 n에서 y값 종류를 k라고 할 때 전체 시간복잡도는 $O(n + k)$이다.

class Solution:
    def countTrapezoids(self, points: List[List[int]]) -> int:
        freq = Counter(p[1] for p in points)    # 각 y좌표별 점 개수 세기
        Sum, c2 = 0, 0                           # Sum: 모든 수평선 수의 합, c2: 각 층의 수평선^2 합

        for f in freq.values():                  # y좌표별 점 개수 반복
            if f <= 1:                           # 점이 1개 이하라면 수평선이 없음
                continue
            c = f * (f - 1) // 2                 # 해당 y층에서 만들 수 있는 수평선 수 C(f, 2)
            Sum += c                             # 전체 수평선 누적 합
            c2 += c * c                          # 수평선 수의 제곱 누적 (나중에 중복 제거에 사용)

        # (Sum^2 - Σ c_i^2) / 2 = 서로 다른 두 y층에서 선택한 수평선 쌍의 개수
        return (Sum * Sum - c2) // 2 % (10**9 + 7)

4. 마무리

아무리 잘 풀리지 않더라도 직접 풀어보는 시간을 갖자.