1. 문제 소개

3583. Count Special Triplets

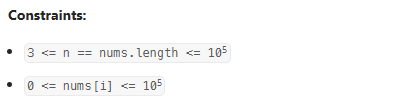
2. 나의 풀이

문제의 힌트는 빈도수 map을 사용해 배열을 한 번 순회할 때, 숫자 좌우에 나오는 값들을 추적하는 것이다.
Counter()를 사용해 순회한 숫자 좌우의 값을 추적해 더해서 풀었다.
시간복잡도는 $O(n)$이다.

class Solution:
    def specialTriplets(self, nums: List[int]) -> int:
        MOD = 10**9 + 7                 # 결과를 나눌 모듈러
        freq_prev, freq_next = Counter(), Counter(nums)
        # freq_prev: 현재 인덱스 이전 구간에 등장한 값들의 빈도
        # freq_next: 현재 인덱스 이후(포함) 구간에 등장한 값들의 빈도 (초기에는 전체)

        ans = 0                          # 정답(특별한 triplet 수)을 누적할 변수
        for n in nums:                   # nums를 왼쪽에서 오른쪽으로 한 번 순회
            target = 2 * n               # 가운데 값 n을 기준으로 사용할 타깃 값

            # 현재 위치의 값 n을 "가운데 원소"로 사용하려 하므로,
            # freq_next에서는 "아직 처리되지 않은 뒤쪽 구간"에 n이 있다고 가정하고,
            # 이 위치를 지나갈 때 n을 하나 제거하여 "앞으로는 뒤쪽에 없다"고 처리.
            freq_next[n] -= 1

            # 현재 원소 n을 가운데로 두었을 때,
            #   · 앞쪽에서 값이 target인 개수: freq_prev[target]
            #   · 뒤쪽에서 값이 target인 개수: freq_next[target]
            # 이 둘의 곱이, 이 n을 가운데로 갖는 special triplet의 개수가 된다.
            ans = (ans + freq_next[target] * freq_prev[target]) % MOD

            # 이제 n은 앞으로 "이전 구간"에 포함되므로 freq_prev에 반영
            freq_prev[n] += 1

        return ans                       # 누적된 special triplet 수 반환

3. 다른 풀이

다른 풀이는 위치 인덱스를 구축하고, 중앙값을 기준으로 triplet을 검사한 이후에 이진탐색으로 좌우 개수를 세었다.
시간복잡도는 $O(n\, logn)$이다.

class Solution:
    def specialTriplets(self, nums: List[int]) -> int:
        MOD = 10**9 + 7
        pos = defaultdict(list)     # 각 값 v가 등장한 모든 인덱스를 저장하는 딕셔너리

        # pos[v] = v가 등장한 모든 index 의 오름차순 리스트
        for i, v in enumerate(nums):
            pos[v].append(i)

        # arr 안에서 기준 인덱스 i보다 작은 index 개수, 큰 index 개수를 찾는 upper_bound 역할
        # 반환값: (i보다 작은 개수, i보다 큰 개수)
        def upper_bound(arr, i):
            l, r = 0, len(arr) - 1   # arr은 이미 정렬된 상태(인덱스를 순서대로 append했기 때문)
            while l < r:
                mid = l + ((r - l + 1) >> 1)
                # arr[mid] ≤ i 이면 mid까지는 i보다 작은 구간으로 인정
                if i >= arr[mid]:
                    l = mid
                else:
                    r = mid - 1
            # l 은 "i 이하인 마지막 인덱스"의 위치
            return l + 1, len(arr) - 1 - l   # (i보다 작은 개수, i보다 큰 개수)

        ans = 0
        # j = i 를 가운데 원소로 사용 (triplet 형태: (x, i, y))
        for i in range(1, len(nums) - 1):
            target = nums[i] * 2             # special 조건을 만족할 target 값

            # target 이 존재하고, target 인덱스가 최소 2개 이상이며, 앞쪽에도 존재하는 경우 검사
            if target in pos and len(pos[target]) > 1 and pos[target][0] < i:
                # pos[target] 중에서 i보다 작은 개수 l, i보다 큰 개수 r 을 구함
                l, r = upper_bound(pos[target], i)

                # nums[i] == 0 이면 target = 0 인데, 가운데가 포함될 수 있으므로 조정 필요
                # 가운데 index i 를 포함하지 않도록 조정
                if nums[i] == 0:
                    l -= 1   # 나 자신을 제외하여 i보다 작은 개수에서 1 감소

                # 가능한 triplet 수 = (왼쪽 개수 * 오른쪽 개수)
                ans = (ans + l * r) % MOD

        return ans

4. 마무리

오늘은 조금 힘들었지만, 원리를 알고나니 간단해졌다.