1. 문제 소개

1925. Count Square Sum Triples

2. 나의 풀이

푸는 방법은 간단하게 $a^2 + b^2 = c^2$를 적용하면 됐지만, 시간초과가 날까 걱정했다.
다행시 시간초과에 걸리지 않았고, 시간복잡도는 $O(n^2)$이다.

class Solution:
    def countTriples(self, n: int) -> int:
        ans = 0                              # 조건을 만족하는 (a, b, c) triplet 개수를 누적할 변수

        for a in range(1, n+1):              # a를 1부터 n까지 순회
            for b in range(1, n+1):          # b를 1부터 n까지 순회 (a와 독립적으로 전 범위 탐색)
                # a^2 + b^2 값에 대해, 그 근사 제곱근을 이용해 c를 추정
                c = int(sqrt(a * a + b * b))

                # c가 범위 [1..n] 이내이고, c^2가 정확히 a^2 + b^2 와 같다면 조건을 만족하는 triplet
                if c <= n and c*c == a*a + b*b:
                    ans += 1                 # 유효한 (a, b, c) 하나를 찾았으므로 카운트 증가

        return ans                           # 최종적으로 찾은 triplet 개수 반환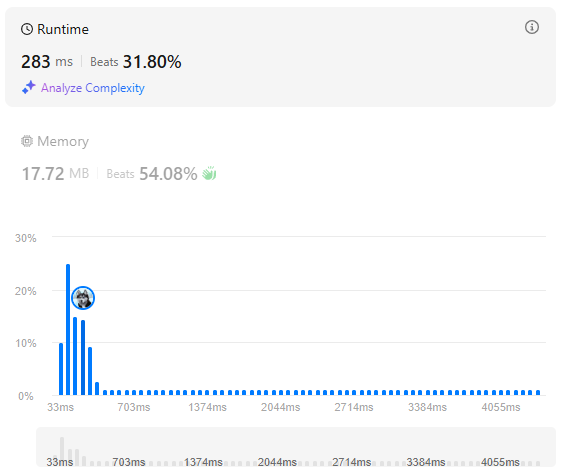

3. 다른 풀이

이 문제는 사실 피타고라스 삼각형을 만족한는 세 숫자를 찾는 것이고, 다음과 같은 공식을 적용할 수 있다.

시간복잡도는 $O(n)$에 근사한다.

from math import sqrt, gcd

class Solution:
    def countTriples(self, n: int) -> int:
        res = 0
        for u in range(2, int(sqrt(n)) + 1):        # u는 피타고라스 정수해 생성 공식의 큰 값
            for v in range(1, u):                   # v는 작은 값 (u > v)
                # (u, v)는 한 쪽만 홀수여야 하고(gcd 조건 포함) 서로소일 때만 primitive triple 생성 가능
                if (u - v) & 1 == 0 or gcd(u, v) != 1:
                    continue

                c = u * u + v * v                   # 피타고라스 삼각형에서 c(빗변)에 해당
                if c > n:                           # c가 n보다 크면 (a, b, c)에서 c ≤ n 조건 불만족
                    continue

                # 한 primitive triple이 k배 확장되면 (ka, kb, kc)도 valid.
                # kc ≤ n  →  k ≤ n // c  →  가능한 k의 개수는 (n // c)
                # (a, b)와 (b, a)는 다른 triple이므로 2를 곱함.
                res += 2 * (n // c)

        return res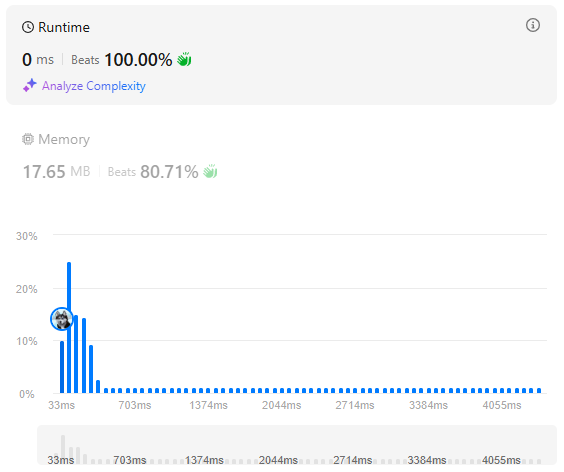

4. 마무리

쉬운 문제였지만 다른 방법을 볼 수 있어 좋았다.