1. 문제 소개

1351. Count Negative Numbers in a Sorted Matrix

2. 나의 풀이

이분탐색을 이용한 풀이다.
시간복잡도는 $O(n * log m)$이다.

class Solution:
    def countNegatives(self, grid: List[List[int]]) -> int:
        ans = 0                                           # 음수 개수 누적
        n = len(grid[0])                                  # 열 개수(각 row 길이)

        for row in grid:                                  # 각 행마다 독립적으로 처리
            left, right = 0, n                            # 이진 탐색 범위: [left, right)

            while left < right:                           # 첫 음수 위치(lower_bound)를 찾는 루프
                mid = (left + right) // 2                 # 중간 인덱스

                if row[mid] < 0:                          # mid가 음수라면, 첫 음수는 mid 포함 왼쪽에 있을 수 있음
                    right = mid                           # 오른쪽 경계를 mid로 당김
                elif row[mid] >= 0:                       # mid가 0 이상이면, 첫 음수는 mid 오른쪽에만 존재
                    left = mid + 1                        # 왼쪽 경계를 mid+1로 이동

            ans += n - left                               # left는 첫 음수 인덱스(없으면 n), 음수 개수는 n-left

        return ans                                        # 전체 음수 개수 반환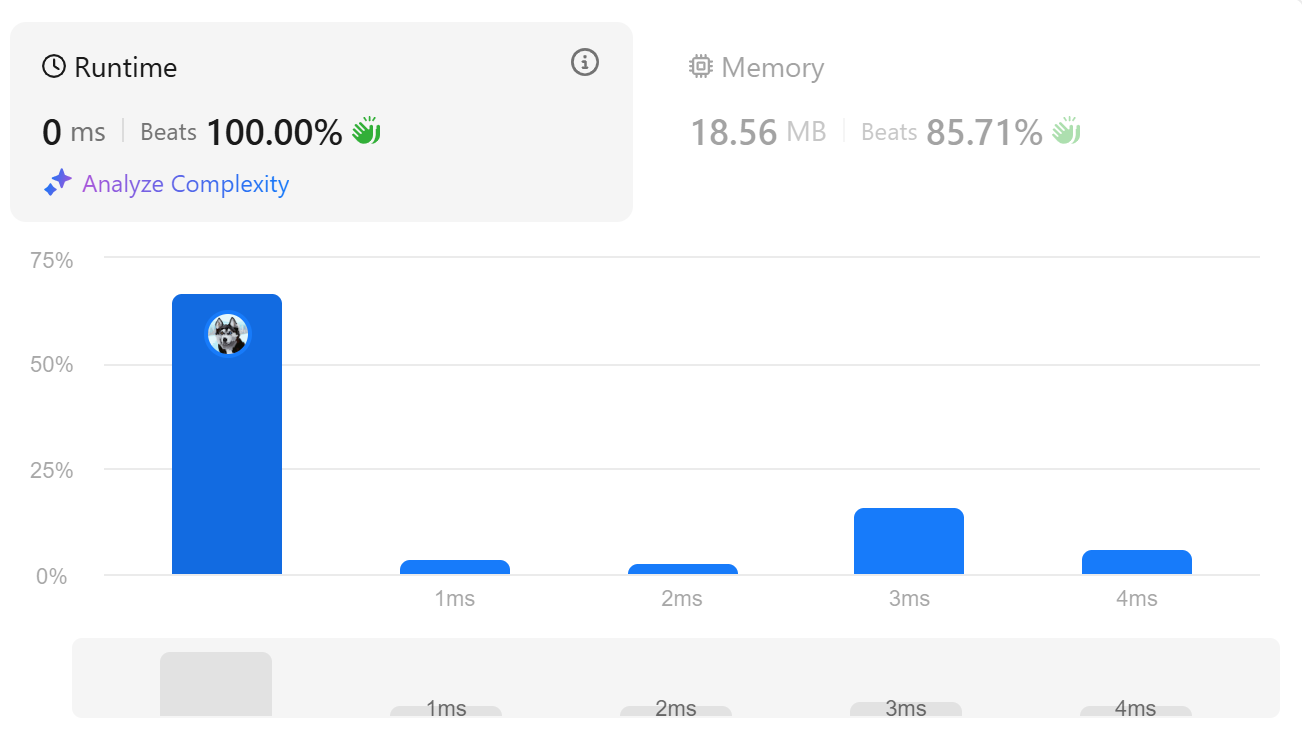

3. 다른 풀이

이미 정렬된 배열임을 이용하여 계단식으로 포인터를 움직여 푸는 방식이다.
이 경우 시간복잡도는 $O(n+m)$이다.

class Solution:
    def countNegatives(self, grid: List[List[int]]) -> int:
        ans = 0                                           # 음수 개수 누적
        n, m = len(grid), len(grid[0])                    # n: 행 개수, m: 열 개수
        i, j = n-1, 0                                     # 좌하단에서 시작(i는 아래에서 위로, j는 왼쪽에서 오른쪽으로)

        while i >= 0 and j < m:                           # 범위 내에서 포인터 이동
            if grid[i][j] < 0:                            # 현재 값이 음수면, 같은 행의 j..m-1은 모두 음수(내림차순 정렬)
                ans += m - j                              # 그 구간을 한 번에 더함
                i -= 1                                    # 위 행으로 이동(다음 행(위쪽)에서도 동일 논리 적용)
            else:                                         # 현재 값이 0 이상이면, 같은 열의 위쪽은 더 크거나 같으므로 음수 아님
                j += 1                                    # 오른쪽으로 이동(더 작은 값 쪽으로 가서 음수를 찾음)

        return ans                                        # 전체 음수 개수 반환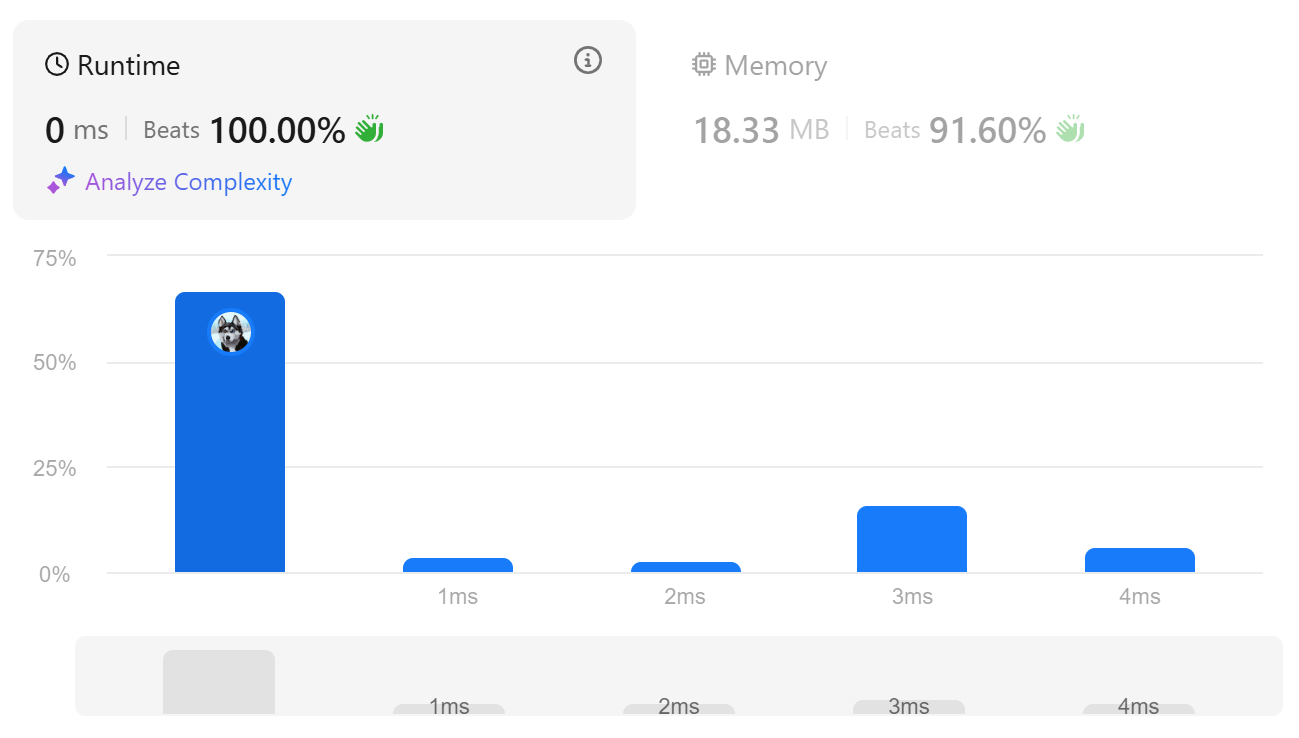

4. 마무리

둘 다 재미있는 풀이었다.
미리 정리된 배열의 힘이 느껴진다.