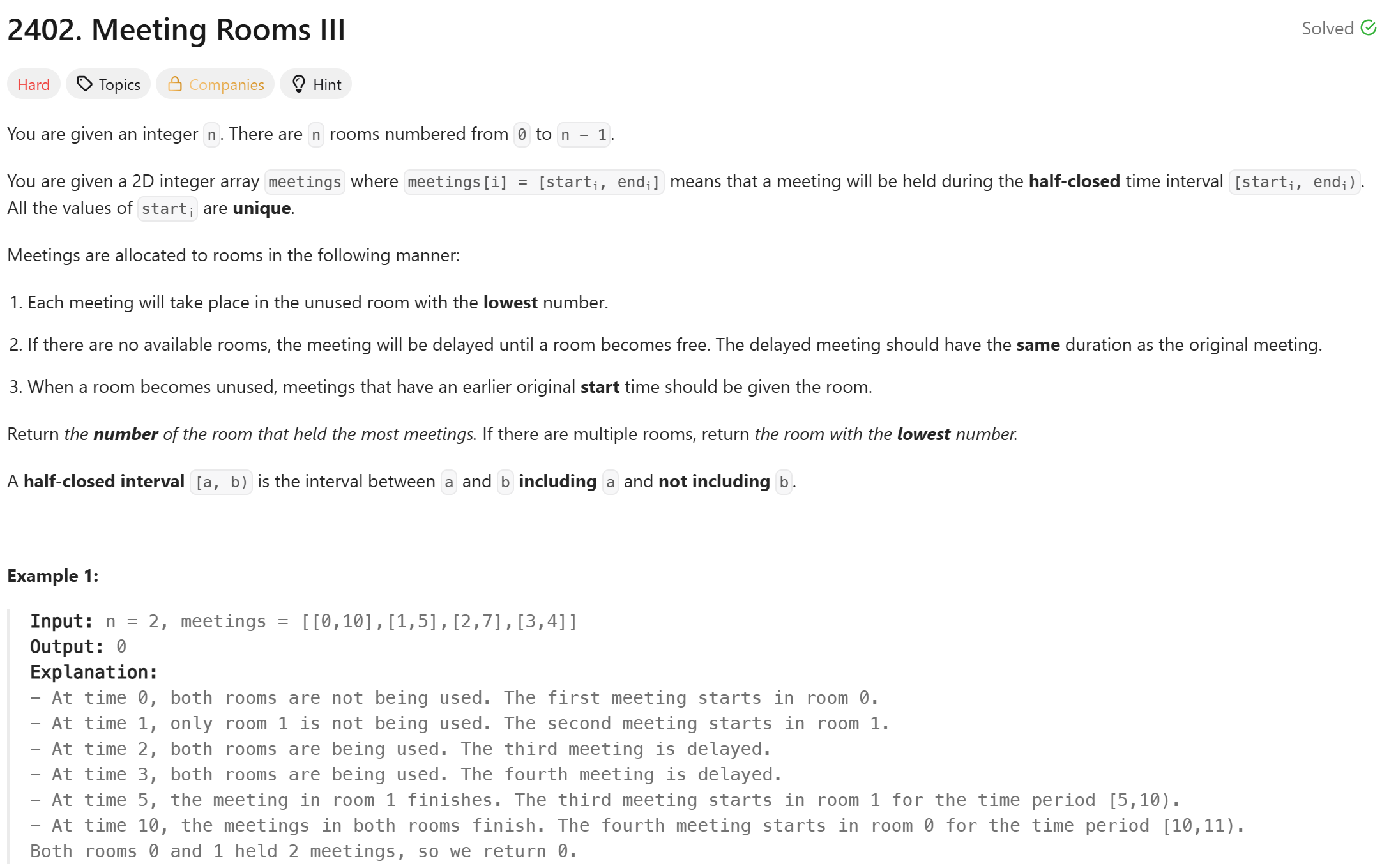
1. 문제 소개

2402. Meeting Rooms III

2. 나의 풀이

풀지 못했다.

3. 다른 풀이

Editorial의 풀이는 다음과 같다.
시간복잡도는 $O(M log M + M * n)$이다.

class Solution:
    def mostBooked(self, n: int, meetings: List[List[int]]) -> int:
        room_availability_time = [0] * n                 # 각 회의실이 다음으로 비는 시각(초기에는 모두 0)
        meeting_count = [0] * n                          # 각 회의실이 배정받은 회의 횟수 카운트

        for start, end in sorted(meetings):              # start 기준 정렬(동률이면 end 기준) 후 순서대로 처리
            min_room_availability_time = inf             # (사용 가능한 방이 없을 때) 가장 빨리 비는 시간 추적용
            min_available_time_room = 0                  # 가장 빨리 비는 방의 인덱스
            found_unused_room = False                    # start 시점에 즉시 배정 가능한 방을 찾았는지 여부

            for i in range(n):                           # 모든 방을 선형 탐색
                if room_availability_time[i] <= start:   # 이 방이 start 시점에 비어 있으면
                    found_unused_room = True             # 즉시 배정 가능
                    meeting_count[i] += 1                # 해당 방의 회의 수 증가
                    room_availability_time[i] = end      # 이 방은 end 시각까지 사용됨
                    break                                # "가장 작은 번호 방"이 우선이므로 첫 발견 즉시 종료

                # 즉시 배정 가능한 방이 없는 경우를 대비하여,
                # 가장 빨리 비는 방(availability가 최소인 방)을 추적
                if min_room_availability_time > room_availability_time[i]:
                    min_room_availability_time = room_availability_time[i]
                    min_available_time_room = i

            if not found_unused_room:                    # start 시점에 비어 있는 방을 못 찾은 경우
                room_availability_time[min_available_time_room] += end - start
                                                        # 가장 빨리 비는 방에서 기다렸다가,
                                                        # 회의 길이(end-start)만큼 종료 시간을 연장
                meeting_count[min_available_time_room] += 1
                                                        # 해당 방의 회의 수 증가

        return meeting_count.index(max(meeting_count))   # 최대 회의 수를 가진 방의 인덱스 반환(동률이면 가장 작은 인덱스)

4. 마무리

시간이 부족하기도 했고 어렵기도 했다.
다음에는 내가 직접 풀어야겠다.