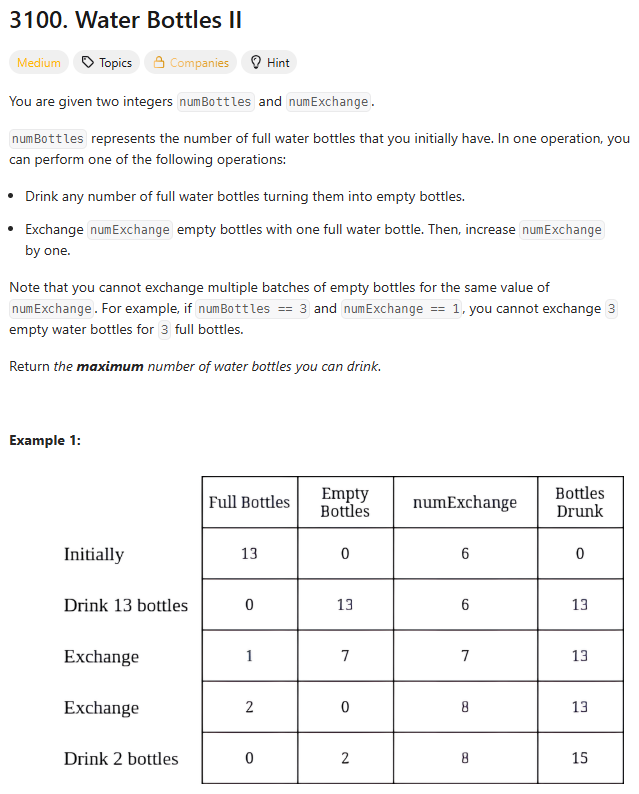
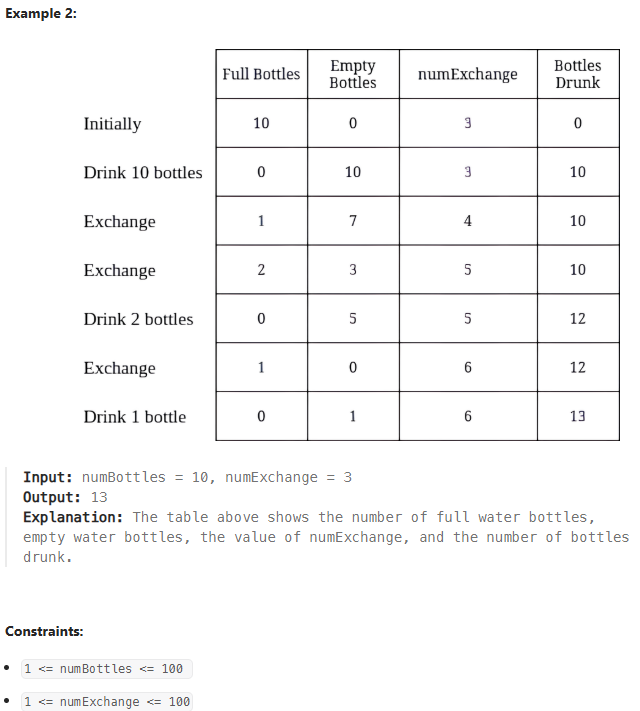
1. 문제 소개

3100. Water Bottles II

2. 나의 풀이법

어제와 비슷하지만, 교환에 필요한 빈 병이 계속 늘어나는 차이점이 존재한다.

class Solution:
    def maxBottlesDrunk(self, numBottles: int, numExchange: int) -> int:
        answer = 0
        while numBottles > 0:
            if numBottles >= numExchange:
                numBottles -= numExchange - 1
                answer += numExchange
                numExchange += 1
            else:
                answer += numBottles
                numBottles = 0
        return answer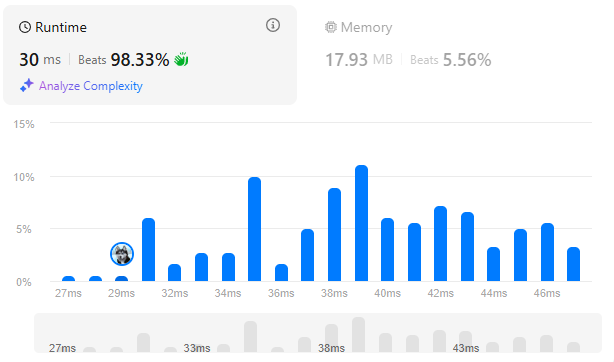

한 번에 좋은 성적을 거두었다.
내 풀이의 시간복잡도는 $O(n)$정도라고 할 수 있다.

3. 다른 풀이법

class Solution:
    def maxBottlesDrunk(self, numBottles: int, numExchange: int) -> int:
        ans = numBottles
        empty = numBottles
        while empty >= numExchange:
            ans += 1
            empty -= numExchange - 1
            numExchange += 1
        return ans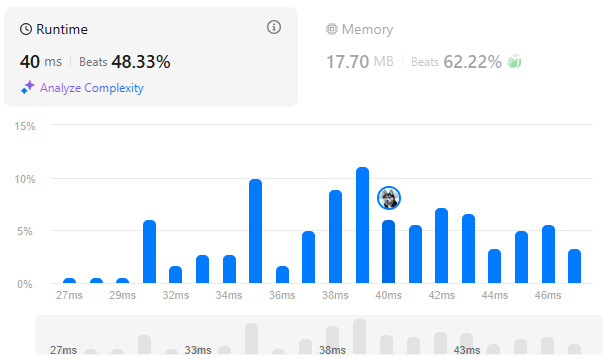

내 풀이와 비슷하지만 조금 다르다.
나는 매 루프마다 교환을 1번씩 처리하기에, 교환횟수에 시간복잡도가 비례하지만,
Editorial의 경우에는 교환횟수마다 numExchange가 1씩 커지기 때문에 시간복잡도가 $O(\sqrt n)$으로 줄어들게 된다.

4. 결론

class Solution:
    def maxBottlesDrunk(self, numBottles: int, numExchange: int) -> int:
        a = 1
        b = 2 * numExchange - 3
        c = -2 * numBottles
        delta = b * b - 4 * a * c
        t = math.ceil((-b + math.sqrt(delta)) / (2 * a))
        return numBottles + t - 1

아예 계산식을 구현해 시간복잡도를 $O(1)$로 만드는 방식도 존재한다.
결국 생각을 얼마나 깊게 하는가의 차이인 것 같다.