드디어 벼르고 벼르던 2022 카카오 인턴 문제를 풀었다. 처음 문제를 봤을때는 대체 이게 뭐지 하고 너무 어지러웠고 푸는 방법이 도저히 생각나지 않았다. 그래서 이 전 포스팅에서 올렸던 합승택시 요금 문제를 다시한번 풀어봤고 비록 크게 도움은 안됐지만 알고리즘의 기본 이해와 오랜만에 빡쌔게 하는 그래프 탐색을 해보니 기분이 좋았다.
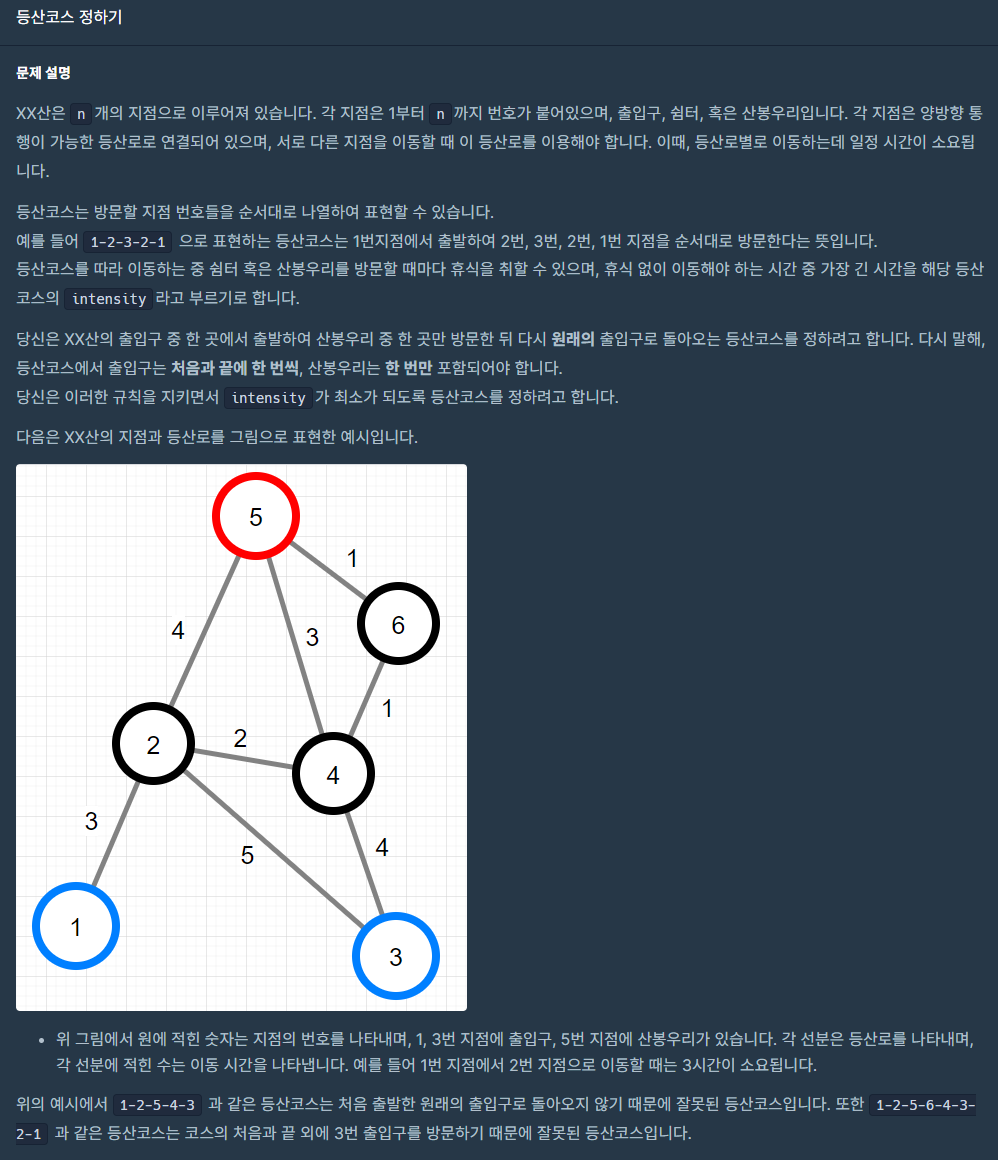
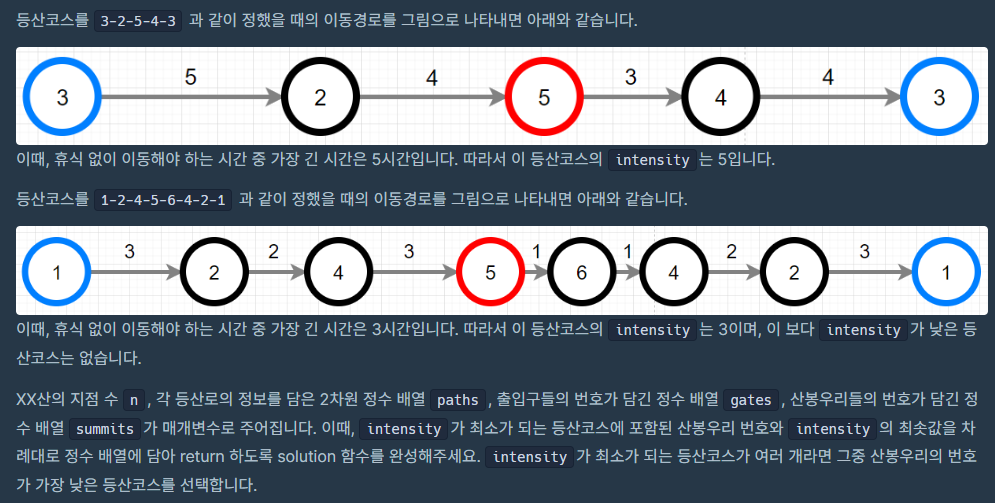
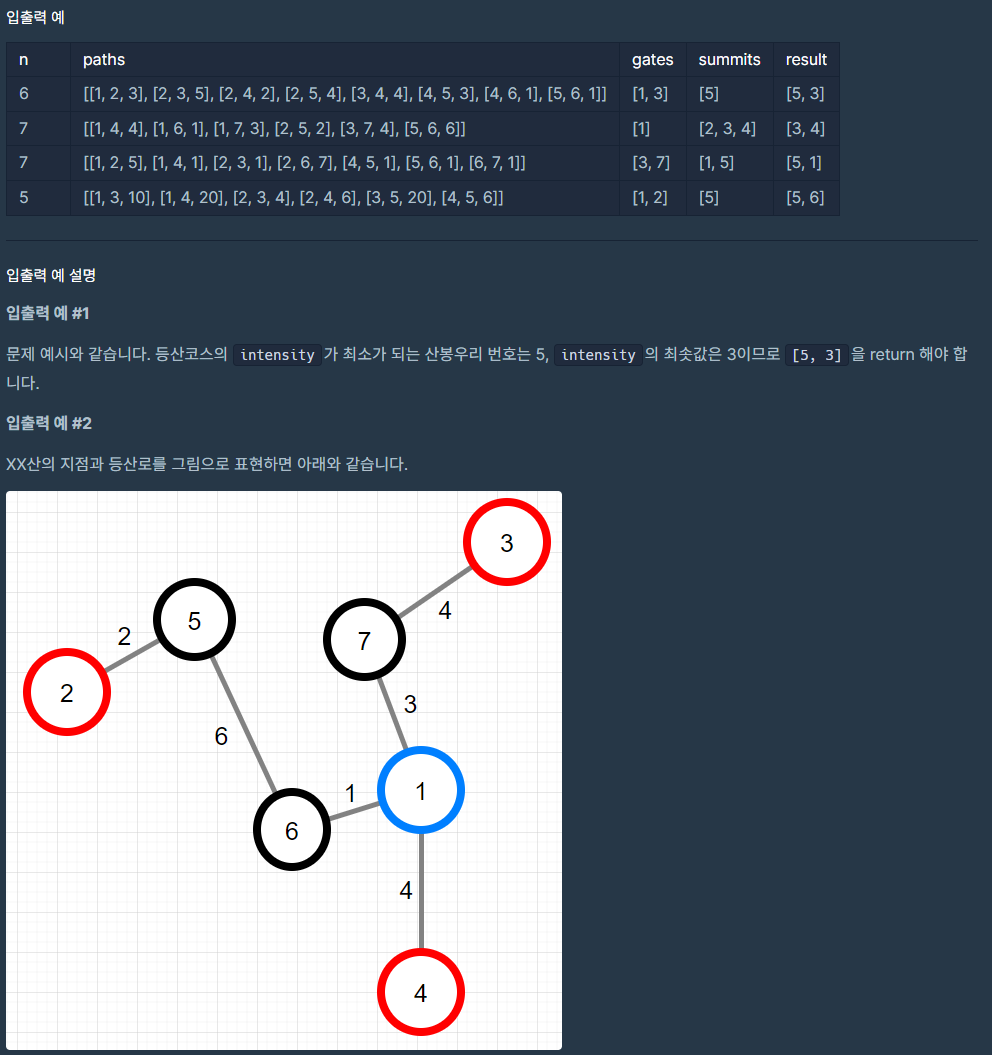
문제는 설명하기에는 너무 복잡할 정도로 문제가 길었는데 카카오는 좋은게 문제를 낼때 설명 자체가 굉장히 디테일해서 예시로 참고하기 좋다. 간단히 설명해서, entrance 로 들어갈 수 있는 노드가 따로 존재하고 summit 이라고 불리는 노드가 따로있다. 각 entrance 에서 출발 했을때 적합한 등산코스를 만들어야 하는데 이때 중요한건 intensity 라는 요소가 들어간다는 것이다. 각 edge 는 등산을 하는데 필요한 시간이고 쉬지 않고 등산코스를 만든다고 할때 이 시간이 최소화 되는 루트가 필요하다. 추가적으로 루트를 만들때 summit 이라고 불리는 노드가 꼭 하나 들어가야한다. 정리하자면,
- Intensity, 즉 등산에 필요한 시간이 최소화 되야한다
- Summit 노드는 단 "한번" 들어가야한다
- Entrance 로 분별되는 노드는 루트에 중복 되면 안된다.
솔직히 문제를 읽었을때 다익스트라가 가장 먼저 생각이 났다. 왜냐면은 등산로를 표현한 edge 에 시간이 다 달랐고 최소한의 intensity 를 구하는 문제였기 때문이다. 그런데 문제를 풀고 테스트케이스를 여러번 도전하고 나니 느꼈던 점은 단순 다익스트라가 아니였다.
이 문제는 등산에 필요한 최소 시간을 구하는거지 등산에 필요한 경로에 시간을 합친 최소를 구하는게 아니다. 일반적인 다익스트라는 내가 있는 현재위치 + 경로의 값이 다음 경로가 가진 시간보다 적으면은 경로를 계속 업데이트 해주는 방식인데 이 문제는 경로에 필요한 등산시간을 더하는게 아니고 각 노드마다 필요한 최소 등산 시간을 업데이트 해줬어야 했다. 변형된 다익스트라의 방법을 설명할때 더 자세히 적겠다.
그리고 2번과 3번의 조건을 성공시키기 위해 내가 생각했던 방법은 map 을 이용하는 거였다.
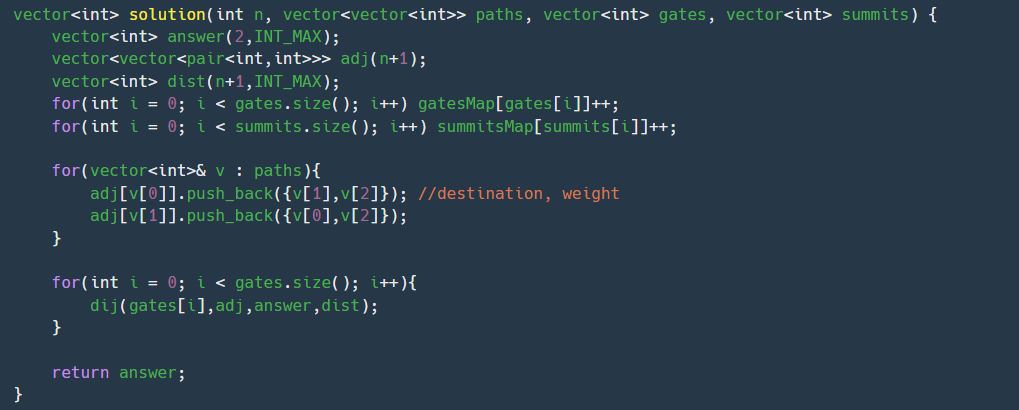
그래프를 연결 해주는것은 간단하다. 다만 나는 gatesMap, summitsMap을 글로벌로 만든후에 모두 저장해주었다. 그리고 entrance 를 읽으면서 해당 entrance, 그래프, 답, 거리표 를 넣어주었다.
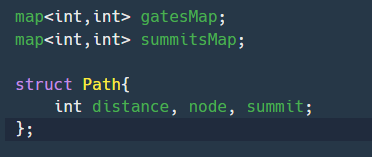
백준에서 그래프 탐색하던 방법이 익숙해서 이렇게 글로벌로 스트럭트를 만들어주었다.
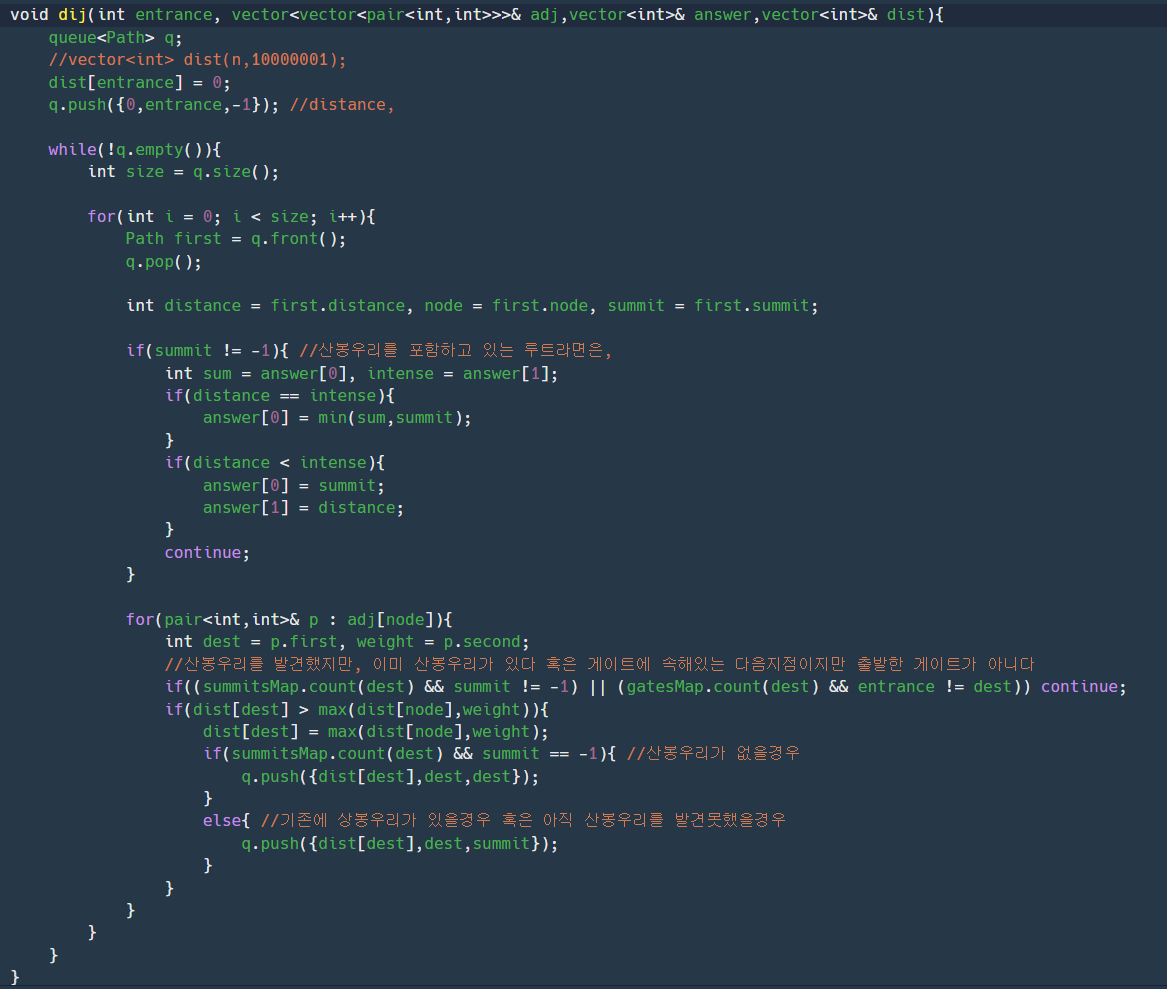
내 다익스트라 코드이다. 몇가지 주시할 점은 일반적인 다익스트라 코드에 쓰이는 priority_queue 를 안쓰고 일반 queue 를 썼다는 점이다. 코드를 좀 설명하자면은 다익스트라와 굉장히 유사하다, 그렇지만 문제에 조건에 맞춰서 조금씩 변형 해주었다.
먼저,
if(summit != -1){ //산봉우리를 포함하고 있는 루트라면은,
int sum = answer[0], intense = answer[1];
if(distance == intense){
answer[0] = min(sum,summit);
}
if(distance < intense){
answer[0] = summit;
answer[1] = distance;
}
continue;
}이 부분은 산봉우리를 포함하는 루트를 뜻한다. 산봉우리가 하나라도 포함되있다면 사실 그 루트는 이미 가능한 루트이기 때문에 answer[0] 과 answer[1] 을 계속 업데이트 해주었다.
for(pair<int,int>& p : adj[node]){
int dest = p.first, weight = p.second;
//산봉우리를 발견했지만, 이미 산봉우리가 있다 혹은 게이트에 속해있는 다음지점이지만 출발한 게이트가 아니다
if((summitsMap.count(dest) && summit != -1) || (gatesMap.count(dest) && entrance != dest)) continue;
if(dist[dest] > max(dist[node],weight)){
dist[dest] = max(dist[node],weight);
if(summitsMap.count(dest) && summit == -1){ //산봉우리가 없을경우
q.push({dist[dest],dest,dest});
}
else{ //기존에 상봉우리가 있을경우 혹은 아직 산봉우리를 발견못했을경우
q.push({dist[dest],dest,summit});
}
}
}이 코드가 가장 중요한 코드라고 생각한다. summitMap 과 gatesMap 을 활용해서 주석에 적은거와 마찬가지로 적당한 조건에서 skip 을 해줬다. 그리고 dist[dest] 를 업데이트 하는 과정에서 해당 노드가 가진 최소 등산시간 혹은 등산루트에서 필요한 시간에 가장 큰 값을 계속 저장해주었다. 그리고 산봉우리가 있고/없고에 차이로 queue 에 다른 값을 넣어주었다.
결론적으로 queue 를 썼던 이유는 우리가 굳이 최소 등산루트 시간 위주로 탐색할 필요가 없었기 때문이다. 결국 산봉우리를 지나는 루트에서 가지고 있는 최소 값이 중요했기 때문에 pq 를 썼을경우 21번 테스트 케이스에서 시간초과가 났었다.
내가 이 문제에서 너무 고전했던거는 놀랍게도 너무 멍청한 이유였다.
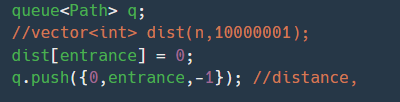
다익스트라를 함수로 만들었고 distance 노드를 계속 초기화 했기 때문이다. 계속 초기화 할 경우 각 entrance 를 지날때마다 결국 모든 노드를 다시 탐색하는 것이기 때문에 시간초과가 날 수 밖에 없었고 저거 하나 고치니깐 전부 통과했다.
어려운 문제라고 생각했는데 풀어보고 나니 쉬워보여서 아쉽다. 그래도 뿌듯했다.
배운점:
1. 다익스트라를 함수로 만들때 절대 distance 벡터를 초기화 하지말자 (필요한 경우 아니면)
2. pq 로 시간초과가 계속 난다면 queue 를 대신 써볼것
