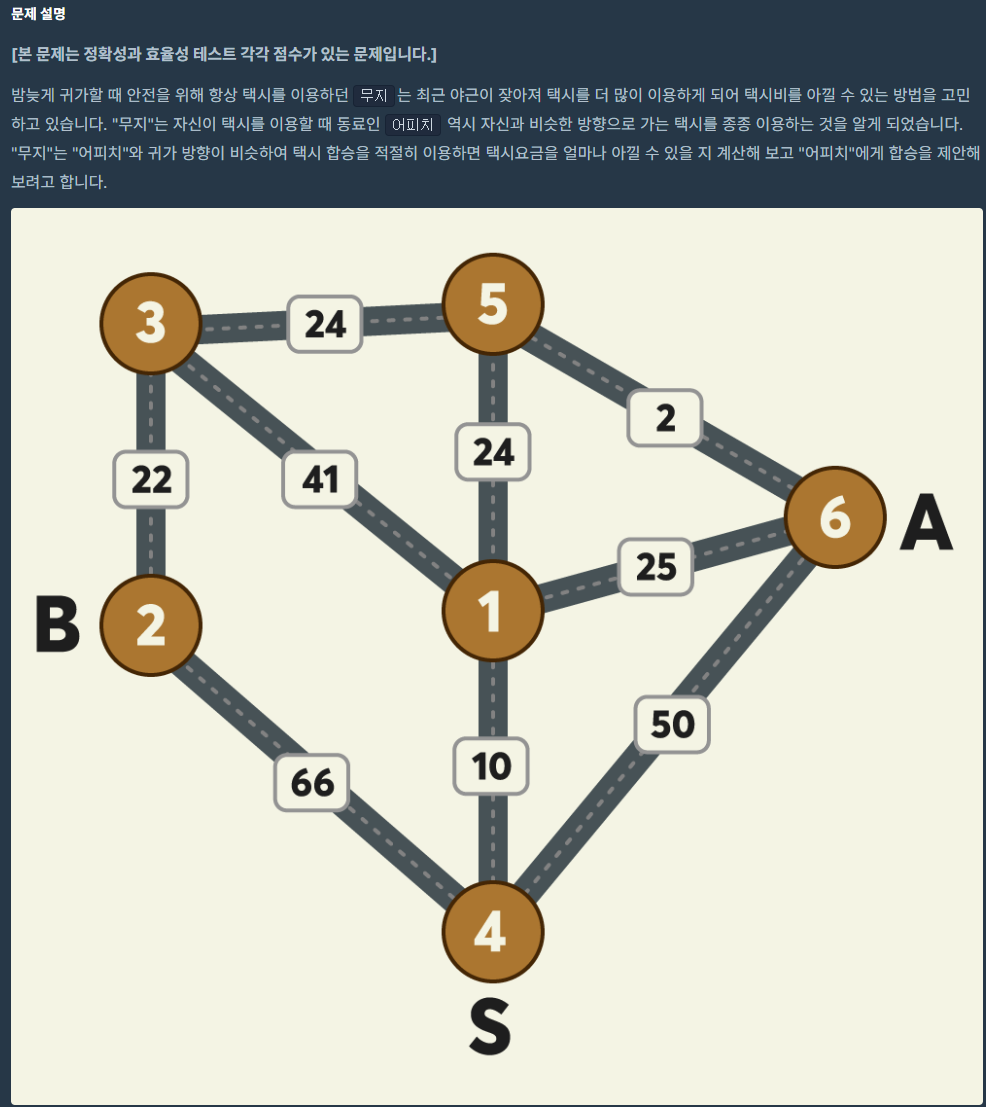

가장 짧은 경로를 구하는 다익스트라 문제를 풀어보고 싶었다. 최근에 경로탐색 문제에 빠져서 많이 풀게되는거 같은데 계속 도전해보고 싶은 마음이 크다.
이번 문제는 내가 GP 에서 있을때 풀어볼려고 시도했던 문제였는데 테스트케이스도 통과하지 못하고 포기하고 답을 봤던 문제였다.
시간이 꽤 지났고 문제를 다익스트라로 다시 풀어봤는데 적어도 테스트케이스는 내 힘으로 모두 통과했지만 전체 테스트 케이스에서 통과를 못했다.
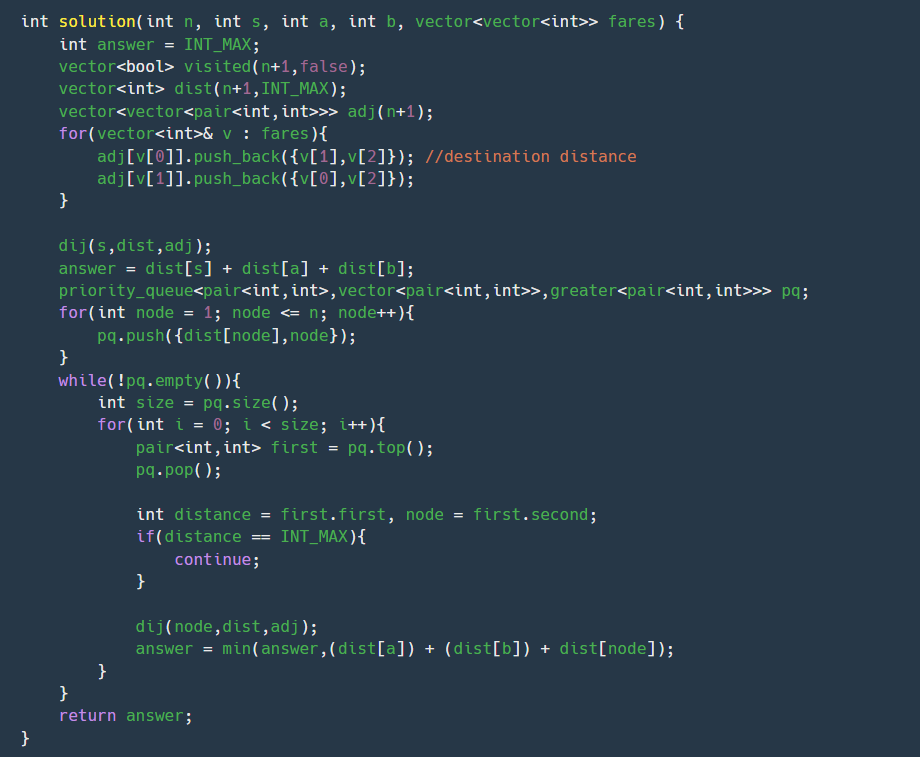
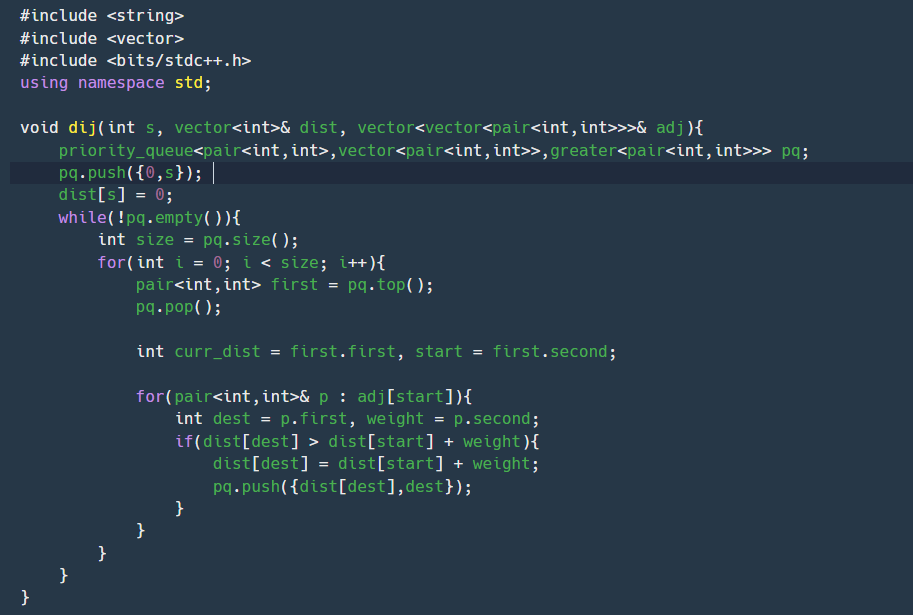
내가 실패한 코드고 조금 더 면밀히 분석해보고 싶었다. 일단 이 문제는 단순한 최소 경로 구하는 문제는 아니고 모든 정점에서 합승을 했다/안했다 가정하에 짧은 경로를 구하는 것이었다. 그리고 양방향으로 이어진 그래프였기 때문에 서로 연결해준 과정은 기본으로 깔아두겠다.
다익스트라를 구현했지만 테스트 케이스 외에는 실패했다. 그리고 그 원인중 하나로는 분명 어떤 테스트 케이스에서 나오는 가중치가 조금은 까다로웠을수도 있다.
솔직히 원인은 잘 모르겠다..
그런데 생각해보면 훨씬 더 쉽게 구할수 있는 다익스트라 방법이 있는데 내가 출발 하는 정점을 s 로만 두는게 아니고 a 와 b를 출발점으로도 두는 것이다. 기본적으로 다익스트라는 출발점에서 시작한 모든 정점을 가장 짧은 구간으로 저장할수 있는 메리트가 있고 s 출발점에 가장 짧은 루트, a 출발점에 가장 짧은 루트, b 출발점에 가장 짧은 루트를 다 따로 저장해두고 각 출발점에 저장된 모든 루트를 더 했을때 가장 짧은 구간이 합승 요금의 최저점 이었다.
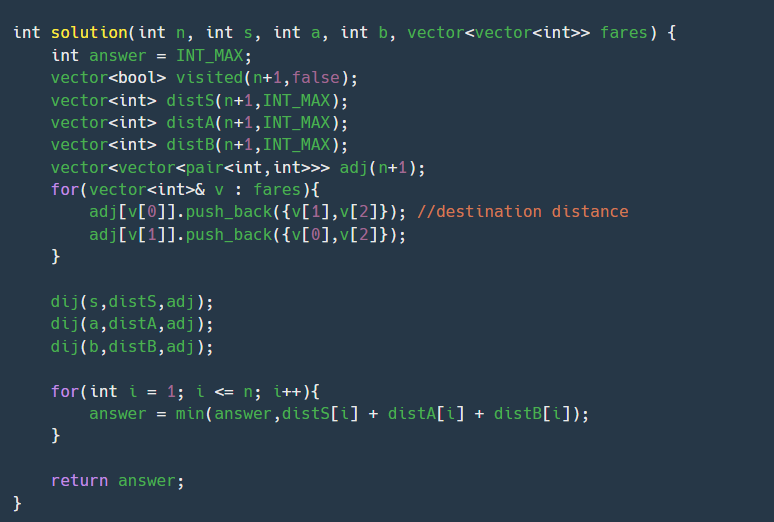
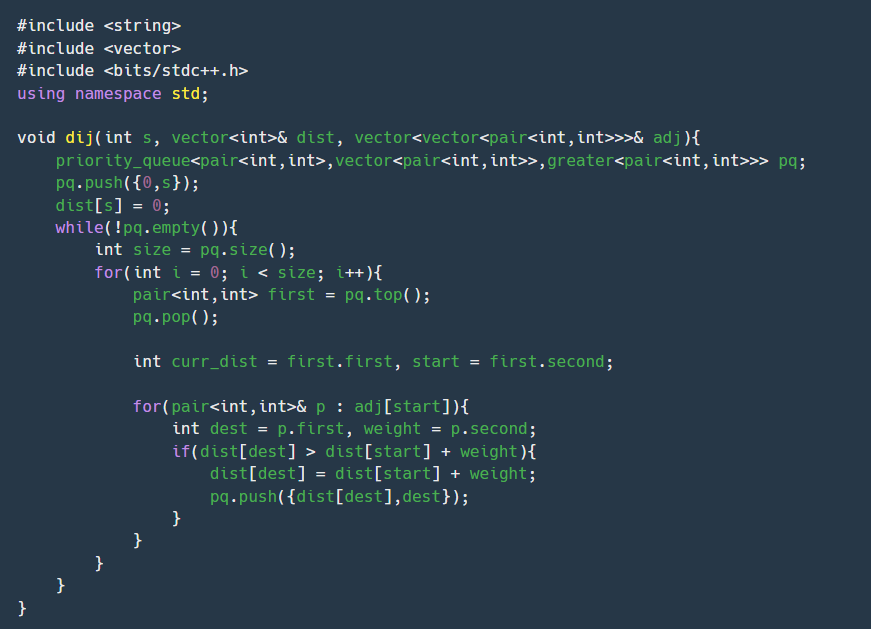
내가 실수한점은 visited 를 따로 구현 안해도 됐었는데 왜 썼는지 모르겠다. 결국 다익스트라에서 그래프 탐색 시점은 그 해당점에 거리가 더 짧을때인데 visited 는 아무 연관이 없었다. 이렇게 보면 꽤 쉬운 문제인데 너무 고전했던거 같고 이렇게 모든 정점에서 찾는 가장 짧은 루트는 플로이드 와샬 알고리즘이 더 적합했던거 같다.
배운점:
1. 다익스트라의 활용
2. 플로이드 와샬 알고리즘 공부 필요성
