리코체 로봇

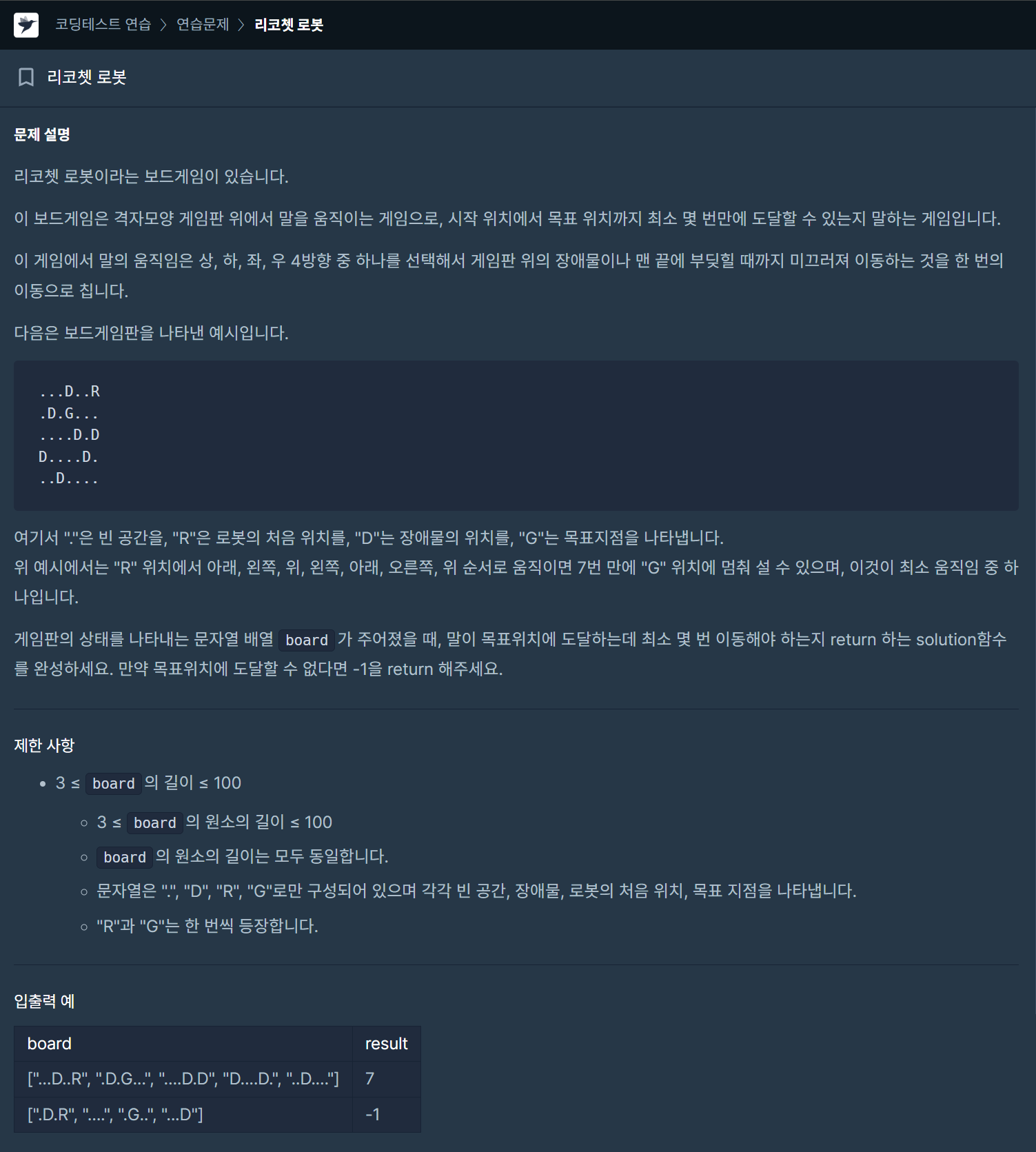
예전에..Leetcode 프리미엄 문제에서 봤던 굉장히 굉장히 비슷한 문제다.

일반적으로 우리가 아는 BFS에서 하나씩 상하좌우로 움직이는 로직이랑 다르게 이 문제는 한번 움직일때 무조건 끝까지 갈 수 있다는 로직이 붙어 있다.

이걸 구현하기 위해서.. 단순하게 룹을 사용했고 조건을 맞춰서 내가 원하는 지점에 도착할 수 있게 했다.

"가장 짧게 도착할 수 있는 구간을 구하시오" BFS, 이동할 수 있는 구간에서 가장 짧게 도착할 수 있는 루트는 BFS + 다익스트라 구현이 필요한거같다.

#include <string>
#include <vector>
#include <bits/stdc++.h> 
using namespace std;

struct Robot{
  int x, y, dist;   
};

vector<pair<int,int>> dir = {{0,1},{0,-1},{1,0},{-1,0}}; 

int solution(vector<string> board) {
    int answer = -1;
    queue<Robot> q; 
    vector<vector<bool>> visited(board.size(), vector<bool>(board[0].size(),false)); 
    for(int i = 0; i < board.size(); i++){
        for(int j = 0; j < board[i].size(); j++){
            if(board[i][j] == 'R'){
                q.push({i,j,0}); 
                visited[i][j] = true; 
                break; 
            }
        }
    }
    
    
    while(!q.empty()){
        int size = q.size(); 
        for(int i = 0; i < size; i++){
            Robot robot = q.front();
            q.pop(); 
            
            int x = robot.x, y = robot.y, dist = robot.dist; 
            
            //cout << x << ' ' << y << ' ' << dist << endl; 
            
            if(board[x][y] == 'G') return dist; 
            
            for(pair<int,int>& p : dir){
                int nX = x + p.first;
                int nY = y + p.second; 
                
                //if(nX < 0 || nY < 0 || nX >= board.size() || nY >= board[0].size() || board[nX][nY] == 'D' || visited[nX][nY]) continue; 
                while(nX >= 0 && nY >= 0 && nX < board.size() && nY < board[0].size() && board[nX][nY] != 'D'){
                    nX += p.first;
                    nY += p.second; 
                }
                
                nX -= p.first;
                nY -= p.second; 
                
                //visited[nX][nY] = true; 
                
                if(!visited[nX][nY]){
                    q.push({nX,nY,dist + 1}); 
                    visited[nX][nY] = true; 
                }
            }
        }
    }
    
    
    return answer;
}