[cs231n+michigan DL for CV] lecture 2: Image Classification (1)

지유경·2024년 7월 2일

CV Computer Vision DL cs231n

2024 Summer Seminar: Computer Vision

목록 보기

1/1

Image classification: A core computer vision task

What is Image Classification?

이미지 분류는 컴퓨터 비전의 중요한 핵심이다. 예를 들어, 이미지를 입력으로 사용하고 출력으로 레이블 중 하나를 이미지에 할당하는 작업이다.

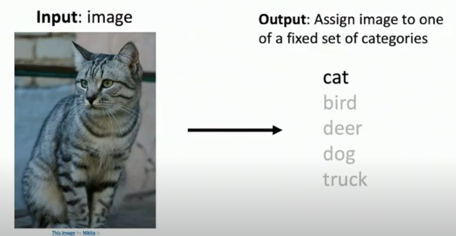
Problem: Semantic Gap

인간에게는 간단한 이미지 분류 작업이 컴퓨터에게는 어려운데, 그 이유는 semantic gap 때문이다. 인간은 이미지를 이미지 자체로 인식하고 직관적으로 이해가 가능하지만, 컴퓨터는 모든 것을 숫자로 인식한다. 컴퓨터에서 이미지는 0~255 사이의 pixel과 red, green, blue의 3개의 채널로 이루어진 거대한 숫자 집합에 불과하다. 이렇게 인간과 컴퓨터가 이미지를 바라보는 인식의 차이를 semantic gap (의미론적 차이)라고 한다.

Challenges: Viewpoint Variation

컴퓨터가 이미지를 숫자로 인식한다는 점에서 발생하는 다양한 문제들이 있다.
1. Viewpoint Variation
카메라를 조금만 움직여도 사진을 구성하는 픽셀 값들이 전부 변한다.

2. Intraclass Variation
유전적 다양성으로 인해 컴퓨터가 이미지 분류 작업이 어려워진다.
예를 들어서, 같은 고양이이지만 색상, 무늬 등의 생김새가 다를 경우 이미지 분류를 하는데 어려움이 생길 수 있다.

3. Fine-Grained Categories
2번과 비슷한 맥락일 수 있는데, 예를 들어서 이는 고양이 안에서도 품종별로 세분화 하는 작업을 일컫는다.

4. Background Clutter
배경으로 인해 식별이 어려운 경우를 말한다. 인식해야할 객체가 배경에 섞일 수도 있기 때문이다.

5. Illumination Changes
장면에서 일어나는 다양한 변화에도 이미지를 잘 분류하려면, 장면의 조명 조건을 변경하면서도 조명 변화에 강인한 분류기가 필요하다. 예를 들어서, 어둠 속에서 사진을 찍을 수도 있고 조명을 켠 채로 찍을 수도 있는 경우를 뜻하는 것이다.

6. Deformation
고양이처럼 변형이 가능한 물체(살아움직이는..) 종류들은 인식하기 더 어려울 수 있다.

7. Occlusion
아래 사진들처럼 고양이의 일부밖에 보이지 않는 상황도 있을 수 있는데, 이 경우에도 인식하기 어려울 수 있다.

Image Classification: Building Block for other tasks!

많은 문제들이 있음에도 불구하고 Image Classification을 연구하는 이유는 다양한 분야에서 유용하게 쓰이기 때문이다. 일례로, 의학 분야에서는 양성 종양과 악성 종양을 구분하는데 이미지 분류 작업을 사용하기도 한다. 그 밖에도 이미지 분류를 사용하여 아래와 같은 작업들이 가능하다.

1. Object Detection
이미지를 분류하는 것에서 어떠한 객체에 대해 Bounding Box를 그려주는 Localization 작업까지 수행할 수 있다.

2. Image Captioning
이미지에 캡션을 달아주는 작업으로, 이미지를 보고 어떤 이미지인지 언어로 설명해주는 작업을 말한다. 접근 방식으로는 크게 'Top-Down Approach'와 'Bottom-Up Approach'로 구분된다.

Top-Down Approach: 이미지를 통째로 시스템에 통과시켜 얻은 요점을 언어로 변환
-> 현재까지 가장 많이 쓰이고 있는 접근방식이지만, 이미지의 디테일한 부분에 집중하는 것이 상대적으로 어렵다.
-> Recurrent Neural Network (RNN)을 활용한 학습이 가능하며, 이 방식의 성능이 가장 좋다고 평가 받는다.
Bottom-Up Approach: 이미지를 부분적으로 접근하여 여러 부분들로부터 단어를 도출하고 이를 결합하여 문장을 생성
-> 이미지의 여러 부분으로부터 하나씩 단어들을 뽑아낸 뒤에 결합하기 때문에 조금 더 디테일한 부분을 반영할 수 있다.

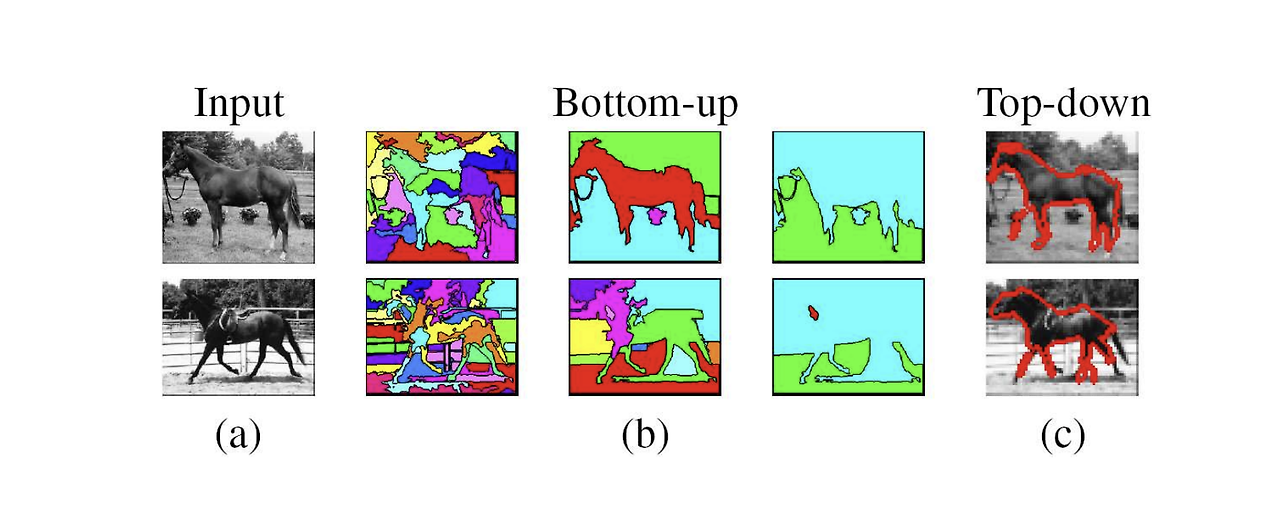
Attempts to Image Classification

이미지 분류를 위해 처음으로 시도된 방법 중 하나는 바로 가장자리 (edge)를 이용하는 것이었다. 가장자리를 추출하여 해당 가장자리의 특성 혹은 패턴을 찾으려고 하는 것이다.

자세히 이야기하면, 가장자리를 따라 outline을 만들어내고, 세 개의 선이 맞닿는 부분을 'corner'라고 정의한다. 고양이, 개 등 객체별 corner 집합의 규칙을 이끌어내 이미지를 구별한다는 것이다. 이 방식에도 문제점이 있는데, 1) Too weak. 고양이로 예를 들면 무늬, 자세 등에 너무 쉽게 영향을 받고, 2) Low scalability. 고양이, 개 등 객체별 집합을 모두 정의해야 하므로 확장성이 낮다.

이 문제점들을 해결하기 위해 등장한 것이 'Data-Driven Approach (데이터 중심 접근법)'이다.

Machine Learning: Data-Driven Approach

Collect a dataset of images and labels
Use Machine Learning to train a classifier
Evaluate the classifier on new images

Nearest Neighbor

분류를 위한 머신러닝 알고리즘으로, 이를 train function과 predict function 두개의 함수를 구현해야 한다.

train function: 모든 training data와 label을 기억한다.
predict function: 입력된 데이터를 training data와 비교함으로써 어떤 label을 가질지 예측한다.

Distance Metric to compare images

입력된 데이터를 training data와 비교하여 어떤 라벨을 가질지 예측하는 함수가 필요한데, 이에 사용할 수 있는 알고리즘 중 하나인 'L1(Manhattan) distance'에 대해서 알아보자.

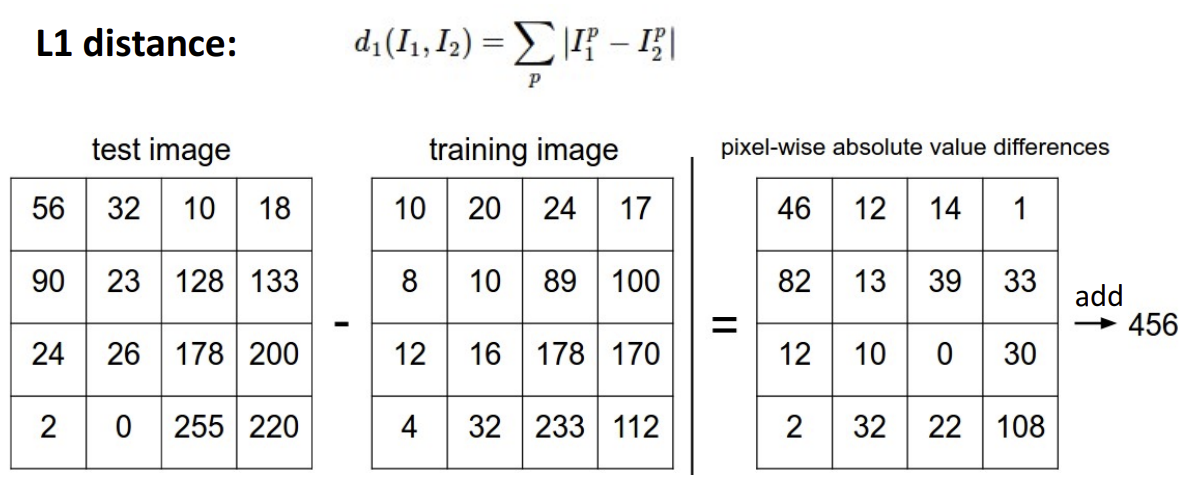
L1 distance 수식을 살펴보면, test image에서 training image 픽셀 값을 빼서 차이를 구하는 것을 볼 수 있다. 각 픽셀끼리의 차를 구한 뒤 결과 값을 합산하는 방식이다.

import numpy as np

class NearestNeibor :
    def __init__(self) :
        pass

    ### Memorize training data
    def train(self , X , y) :
        # X is N x D where each row is an examples. y is label which is 1-dim of size N
        # the nearest neighbor classifier simply remembers all the training data
        self.Xtr = X
        self.ytr = y

    def predict(self , X) :
        # X is N x D where each row is an example we wish to predict label for
        num_test = X.shape(0)
        # let's make sure that the output type matches the input type
        Ypred = np.zeros(num_test, dtype = self.ytr.dtype)

	### For each test image(loop over all test rows)
	### Find nearest training image & Return label of nearest image
	for i in xrange(num_test)
            # find the nearest training images to the i'th test image
            # using the L1 distance (sum of absolute value difference)
            distances = np.sum(np.abs(sel.Xtr - X[i,:]) , axis = 1)
            
            # get the index with smallest distance
            min_index = np.argmin(distances)
            
            # predict the label of nearest example
            Ypred[i] = self.ytr[min_index]
        
        return Ypred

코드를 살펴보면 다음을 알 수 있다.

predict function 정의부의 반복문에서 self.Xtr(입력받은 train data를 사용하여 학습한 내용)과 X[i, :](test data) 의 거리를 합을 구하는 것을 알 수 있다.
이를 통해, L1 distance가 가장 작은 것이 train data와 test data 사이의 차이가 가장 작다는 의미로, 이 차이의 최솟값을 갖는 라벨을 Ypred(결과)로 출력한다.

Problems of Nearest Neighbor

시간 복잡도
Nearest Neighbor에서 train function은 단순히 train data를 저장하므로 O(1)이다. 하지만, predict function에서 반복문을 통해 모든 test data와 train data의 차이를 구하므로 N개의 데이터가 주어졌을 때의 시간 복잡도는 O(N)이 된다. 이는 데이터가 많아질수록 시간 복잡도가 계속해서 증가한다고 볼 수 있다.
Decision Boundaries
Nearest Neighbor는 'Decision Boundaries'를 만들 때 문제가 발생한다.

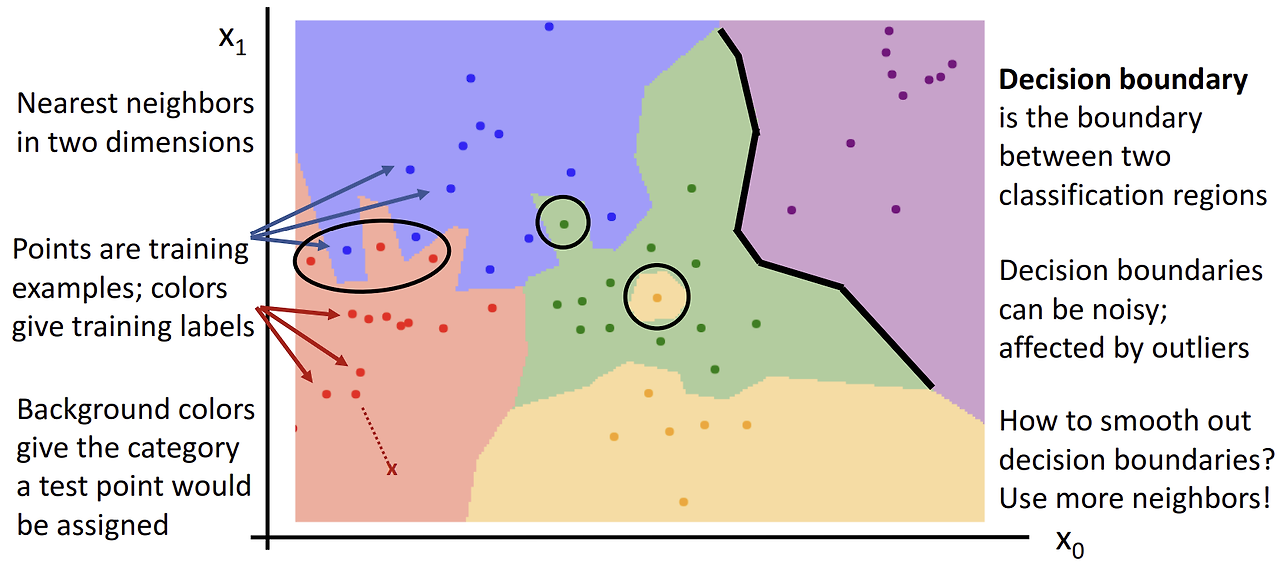
위 이미지에서 각각의 점이 train data이고 점의 색깔은 해당 데이터의 라벨이다. 배경 색은 test data가 주어졌을 때 할당될 라벨이라고 생각하면 된다.

여기서의 문제는

가장 가까운 위치의 데이터만을 이용하여 boundary를 만들기 때문에 이상치에 취약하다.
마찬가지로 가까운 위치의 데이터만을 이용하기 때문에 boundary의 경계면이 부드럽지 못하다. 이럴 경우에는 과적합이 일어날 수 있다.

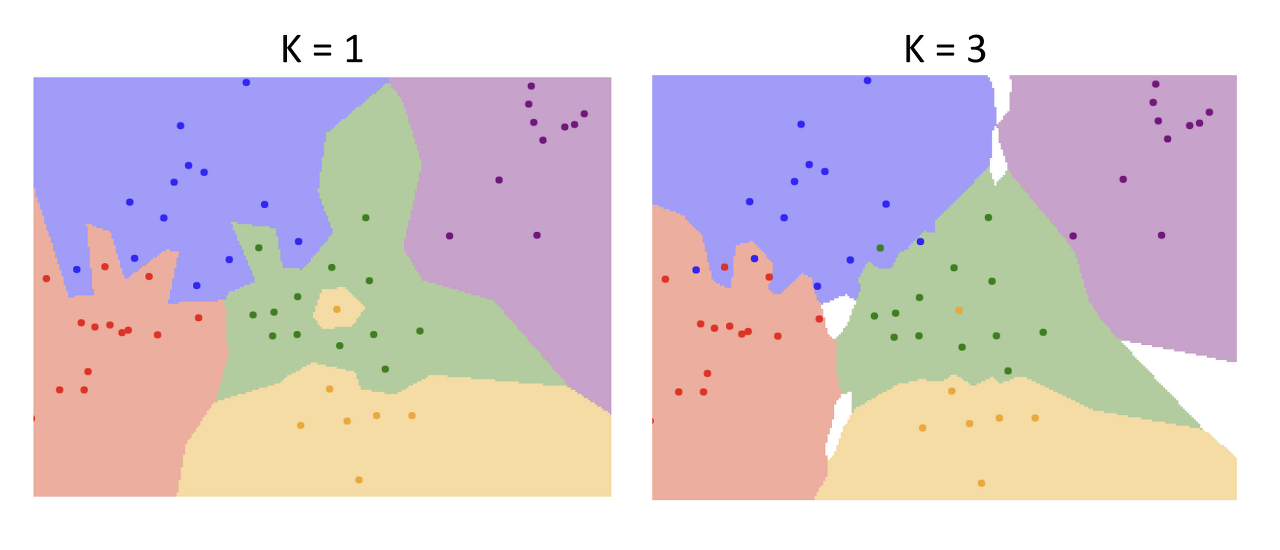
여기서 두번째 문제를 해결하여 경계선을 보다 스무스하게 만들기 위해 생각해낸 것이 'k-nearest neighbor'이다. 단 하나의 이웃만을 이용하는 기존 방식에서 나아가, k개의 이웃을 사용하여 가장 많은 득표수를 가진 클래스로 예측하는 방식이다.

K-Nearest Neighbor

아래의 사진을 통해 k의 수에 따라 경계면이 보다 부드럽게 변화한 것을 확인할 수 있다. 하지만, 경계 사이의 분류되지 않은 공백이 생기는 현상이 발생하는데 이 또한 knn이 해결해야 할 문제 중 하나이다. 공백은 추론하거나 임의로 결정하여 채울 수 있다.

L2 (Euclidean) distance

L1 distance 외에도 L2 (Euclidean) distance가 있다. 어떤 거리 척도를 사용하느냐에 따라서 boundary의 모양에 차이가 생긴다.

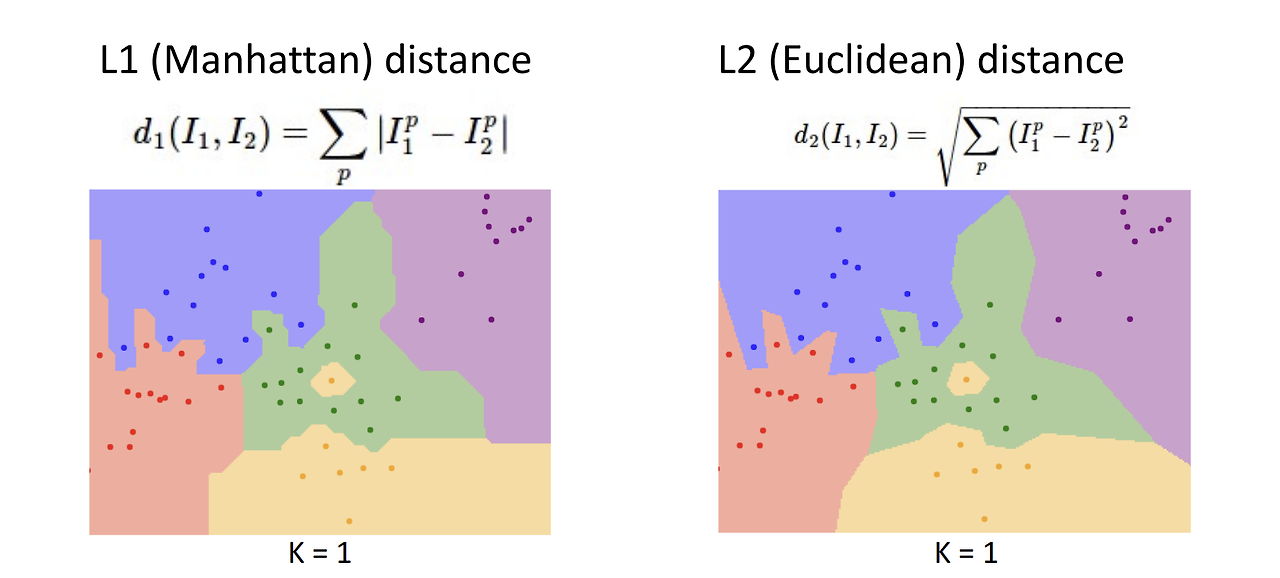
L1 distance: 각각의 벡터 요소들이 개별적인 의미를 가지고 있을 때 사용하는 거리 척도이다.
L2 distance: 벡터 요소들의 의미를 모르거나, 의미가 별로 없을 때 사용하는 거리 척도이다.

실제로 두 거리 척도의 수식을 보면 L1, L2 distance 모두 '거리' 개념이므로 양수가 나와야 한다는 점에서 같지만, 양수를 만들기 위해 사용한 방식이 다른 것을 알 수 있다. L1은 차이에 절댓값을 취하는 방식이라 test data에서 train data를 뺀 값 자체를 보존할 수 있다.

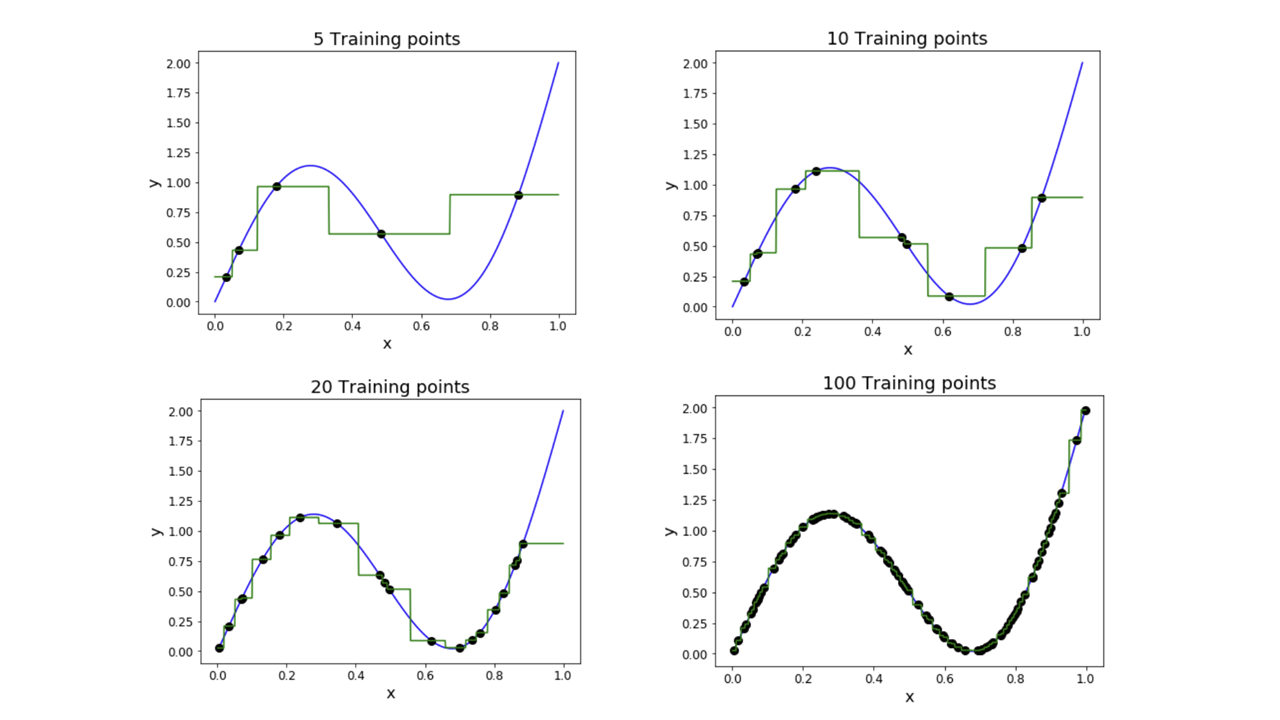
K-Nearest Neighbor의 특징: Universal Approximation

kNN은 충분히 많은 데이터가 주어지고 적절한 k값이 선택된다면, 거의 모든 함수 형태를 근사할 수 있다.(이론적으로는 어떤 함수든 근사할 수 있다고 하지만, 이를 위해서는 몇 가지 조건이 필요하다. 예를 들어, 함수가 특정 도메인에서 연속적이어야 하거나, 훈련 데이터 포인트 간의 간격이 일정해야 한다는 가정 등이 필요하다.) 이는 kNN이 데이터 분포의 세부적인 형태까지 포착할 수 있는 이유 중 하나이다. 또한, 선형 모델이 아니기 때문에 비선형적인 데이터를 잘 처리할 수 있다.

K-Nearest Neighbor의 문제점

- 차원의 저주: 차원이 늘어남에 따라 공간을 균일하게 메우기 위해 필요한 training point의 개수가 기하급수적으로 증가한다. image classification에서 보편적으로 사용하는 데이터셋의 이미지를 분류한다고 생각했을 때, 해당 데이터셋의 이미지 크기는 $32*32$ 이므로 해당 공간을 균일하게 메워 균등한 학습이 이루어지도록 하려면 $2^{32*32}$ 만큼의 training point가 필요하게 된다. image classification에서 kNN 알고리즘을 적용하는 것은 사실상 불가능하다는 뜻이다.