[CS/ Network] 컴퓨터 네트워킹 하향식 접근 8판 5장 네트워크 계층: 제어 평면 5.2 라우팅 알고리즘

5.2 라우팅알고리즘 342
5.2.1 링크 상태(LS) 라우팅알고리즘 344
5.2.2 거리 벡터(DV) 라우팅 알고리즘 348

• 라우팅 알고리즘의 목표 : 송신자부터 수신자까지 라우터의 네트워크를 통과하는 최소 비용 경로(루트)를 결정하는 것
• 라우팅 문제를 나타내기위해 그래프 사용
  • 그래프(graph)는 G(N,E)로 나타냄
  • N : 노드(node)의 집합
    • 네트워크 계층 라우팅 상황에서 그래프상의 노드는 패킷 전달 결정이 이루어지는 지점인 라우터를 나타냄
    • 노드는 각 네트워크를 나타내고 이러한 두 노드를 연결하는 에지는 두 네트워크 간의 연결(피어링(peering))을 나타냄
  • E : 에지(edge)의 집합
    • 노드들을 연결하는 에지는 라우터들 간의 물리 링크를 나타냄
  • 하나의 에지는 집합 N에 속하는 한 쌍의 노드로 표시됨.
    
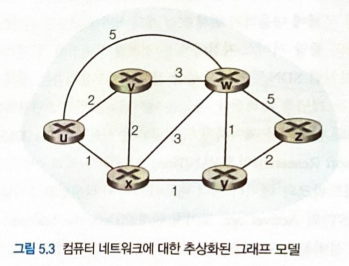
• 에지는 그 비용을 나타내는 값을 가짐
  • 비용 : 일반적으로 해당 링크의 물리 적인 거리, 링크 속도, 링크와 관련된 금전 비용 등을 반영
  • 집합 E에 포함된 어떤 에지（x, y）에 대해 c(x,y)는 노드 x와 y간의 비용을 의미
  • 만약 노드 쌍 (x,y)가 E에 포함되어 있지 않으면 c(x,y）= ∞로 둠
  • 지금은(그림에서) 무방향성 그래프만 고려하는데 방향성 그래프로 확장하는 것도 쉬움
  • 이웃 : 에지（x, y）가 집합 E에 속하면, 노드 y는 노드 x의 이웃이라고 함
• 라우팅 알고리즘의 목표 : 출발지 - 목적지 간 최소비용 찾기
  • 경로 : 그래프 상에서 노드의 연속
  • 경로의 비용 : 경로상 모든 에지 비용의 단순 합
  • 어떤 두 노드 x,y가 주어지면 일반적으로 두 노드 간에 많은 경로가 존재하고 각 경로는 비용을 가짐
  • 최소 비용 경로는 하나일 수도 있고 여러개일 수 있음.
  • 만약 그래프의 모든 에지가 같은 비용을 갖는다면 최소 비용 경로 = 최단 경로
    （즉 출발지와 목적지 사이에서 최소 개수의 링크만을 포함하는 경로）

라우팅 알고리즘을 분류하는 일반적인 방법
첫번째 방식 : 알고리즘이 중앙 집중형인지 분산형인지

• 중앙 집중형 라우팅 알고리즘（centralized routing algorithm)
  • 네트워크 전체에 대한 완전한 정보를 가지고 출발지와 목적지 사이의 최소 비용 경로를 계산
  • 즉，모든 노드 사이의 연결 상태와 링크 비용을 입력값
  • 각 정보는 계산 전 미리 알고 있어야 함.
  • 계산 자체는 한 장소（ex，그림 5.2의 논리적 중앙 집중형 컨트롤러)에서 수행되거나 모든 라우터 각각의 라우팅 모듈로 복사될 수 있음
  • 주요 특징 : 이 연결과 링크 비용에 대한 완전한 정보를 가짐
  • 링크 상태(link-state, LS) 알고리즘 : 전체 상태 정보블 갖는 알고리즘, 네트워크 내 각 링크의 비용읍 알고 있어야 함
• 분산 라우팅 알고리즘(decentralized routing algorithm)
  • 최소 비용 경로의 계산이 라우터들에 의해 반복적이고 분산된 방식으로 수행 됨.
  • 어떤 노드도 모든 링크 비용을 알지X
    • 대신 각 노드는 자신과 직접 연결된 링크에 대한 비용 정보만 가짐
  • ㄴ-> 반복된 계산, 이웃 노드와의 정보 교환 => 최소 비용 경로 계산
  • 거리 벡터(distance-vector,DV) 알고리즘 : 각 노드가 네트워크 내 다른 모든 노드까지 비용(거리)의 추정값을 벡터 형태로 유지

두번째 방식 : 정적 알고리즘과 동적 알고리즘

• 정적 라우팅 알고리즘(static routing algorithm)
  • 경로는 아주 느리게 변함 -> 종종 사람이 개입한 결과
• 동적 라우팅 알고리즘(dynamic routing algorithm)
  • 네트워크 트래픽 부하(load)나 토폴로지(물리적 링크같은 것들) 변화에 따라 라우팅 경로를 변환
  • 주기적으로，혹은 토폴로지나 링크 비용의 변경에 직접적으로 응답하는 방식으로 수행
  • 장점 : 네트워크 변화에 빠르게 대응
  • 단점 : 경로의 루프(loop)나 경로 진동(oscillation) 같은 문제에 취약

세번째 방식 : 라우팅 알고리즘이 부하에 민감한지 아닌지

• 부하에 민감한 알고리즘(load-sensitive algorithm)
  • 링크 비용은 해당 링크의 현재 혼잡 수준을 나타내기 위해 동적으로 변함
  • 현재 혼잡한 링크에 높은 비용을 부과한다면，혼잡한 링크를 우회하는 경로를 택함
• 부하에 민감하지 않은 알고리즘
  • 오늘날 인터넷 라우팅 알고리즘(RIP，OSPF, BGP 등)
  • 링크 비용이 현재(또는 가장 최근)의 혼잡을 반영하지 않기 때문에 민감x

👀 5.2.1 링크 상태(LS) 라우팅 알고리즘

• 네트워크 토폴로지와 모든 링크 비용을 알고있음
• ㄴ 각 노드가 연결된 링크의 식별자와 비용 정보를 담은 링크 상태 패킷을 브로드캐스트하게 함으로써 가능
  • 링크 상태 브로드캐스트(link-state broadcast) 알고리즘에 의해 수행
  • ㄴ-> 모든 노드는 네트워크에 대한 동일하고 완벽한 관점을 가짐
  • ㄴ-> 다른 노드와 똑같은 최소 비용 경로 집합을 계산 가능
• 다익스트라 알고리즘
  • 밀접하게 관련된 알고리즘 : 프림 알고리즘
  • 하나의 노드(출발지, u라고 지칭)에서 네트워크 내 다른 모든 노드로의 최소 비용 경로를 계산
  • 반복적인 알고리즘
    • k번째 반복 : k개의 목적지 노드에 대해 최소 비용 경로가 알려짐
    • 이 k개의 경로는 모든 목적지 노드 경로 중에서 가장 낮은 비용을 가짐
  • D(v)： 알고리즘의 현재 반복 시점에서 출발지 노드부터 목적지 v까지의 최소 비용 경로의 비용
  • p(v): 출발지에서 v까지의 현재 최소 비용 경로에서 v의 직전 노드
  • N'： 노드의 집합. 출발지에서 v까지의 최소 비용 경로가 명확히 알려져 있다면, v는 N'에 포함됨.
• 중앙 집중형 라우팅 알고리즘은 초기화 단계와 반복 부분으로 구성됨.
  • 반복 부분의 수행 횟수 = 네트워크의 노드 수
  • 반복 부분 수행이 종료되면 출발지에서 모든 노드로의 최단 경로 산출

출발지 노드 u를 위한 링크 상태(LS) 알고리즘

1	Initialization:
2 		Nr = {u}
3 		for all nodes v
4 			if v is a neighbor of u
5 				then D (v) = c (ur v)
6 			else D(v) = ∞
7
8 	Loop
9 		find w not in N' such that D (w) is a minimum
10 		add w to N'
11 		update D (v) for each neighbor v of w and not in N’:
12 			D (v) = min (D (v) , D (w) + c (wr v) )
13 			/ * new cost to v is either old cost to v or known
14 			least path cost to w plus cost from w to v */
15 	until = N

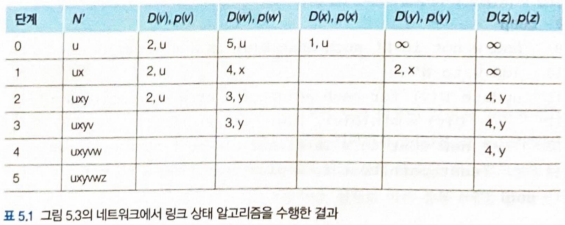
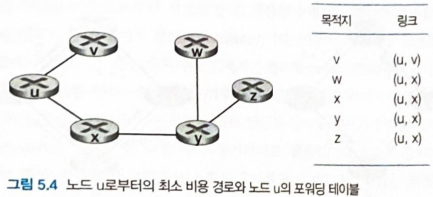
• 그림 5.3의 u에서 목적지까지 모든 최소 비용 경로 계산 과정
  • 표의 각 행은 각 반복이 끝난 후의 알고리즘의 변숫값
  • 그냥 다익스트라 알고리즘이므로 자세한 설명은 생략함. 모르면 구글 검색ㄱㄱ
    
    
• 다익스트라 알고리즘의 계산 복잡도
  • n개의 노드（출발지 노드 제외)가 있다면 최악의 경우 찾아야 하는 노드의 총수
    :n(n + 1）/2 => O(n^2)의 복잡성
  • 힙 데이터 구조를 사용하면 좀더 개선될 수 있음
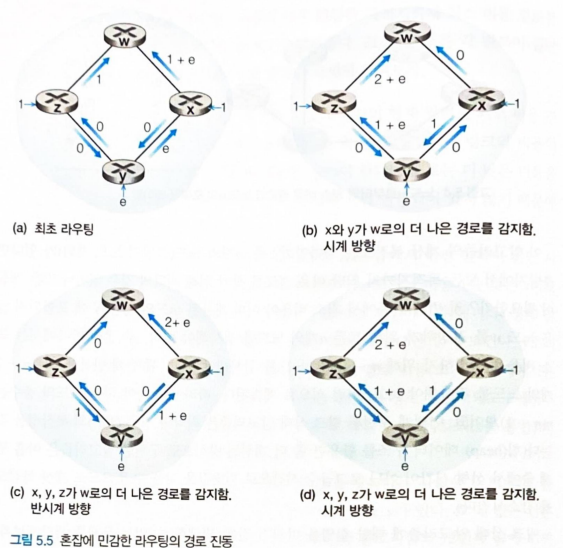
• 발생할 수 있는 진동 문제
  • 링크 비용은 대칭적이지 않음
  • 아래 그림에서 대충 경로 탐지하는 과정중에 최소 비용 경로가 시계방향->반시계방향->시계방향 막 바뀜
• 이러한 진동 문제 해결 방법
  • 1. 링크 비용이 해당 링크가 전달하는 트래픽의 양에 의존하지 않도록 하는 방법
    • 라우팅의 한 가지 목적이 매우 혼잡한 링크를 회피하는 것이므로 떙
  • 2. 모든 라우터가 동시에 링크 상태 알고리즘을 실행하지 못하도록 하는 것
    • 라우터들이 동일한 주기 간격으로 링크 상태 알고리즘을 수행한다 하더라도 각 노드에서의 알고리즘의 실행 시각은 같지않을 것
    • 흥미롭게도 라우터들이 스스로 동기를 맞춤
    • ㄴ= 라우터들이 알고리즘을 각기 다른 시작 시각, 같은 주기를 갖도록 해서 실행하더라도 점진적으로 결국엔 서로 동기화 됨.
    • ㄴ 이러한 자기 동기화는 각 노드가 링크 상태 정보를 송신하는 시각을 임의로 결정하게 함으로써 회피
      

🚗 5.2.2 거리 벡터(DV) 라우팅 알고리즘

• DV 알고리즘의 특징
  • 분산적(distributed) : 각 노드는 이웃으로부터 정보를 받고, 계산을 수행하며，계산된 결과를 다시 그 이웃들에제 배포한다는 점
  • 반복적(iterative) : 이웃끼리 더 이상 정보를 교환하지 않을 때까지 프로세스가 지속된다는 점(자기 종료 가능 : 계산을 멈추라는 신호가 없어도 알아서 멈춤)
  • 비동기적(asynchronous) : 톱니바퀴 돌듯이 모든 노드가 서로 정확히 맞물려 동작할 필요가 없다는 점
• 최소 비용 경로의 비용들 사이의 중요 관계 : 벨만-포드(Bellman-Ford) 식
  노드 x부터 y까지 최소 비용 경로의 비용을 dx(y)이라고 하면,
  dx(y) = minv {c(x, v) + dv(y))
  • minv는 x의 모든 이웃에 적용
  • 직관적
    • x ->v -> y까지의 최소 경로 비용 : c(x, v) + dv(y)
    • 반드시 하나의 이웃 v로 가는 것부터 시작해야 하므로, x에서 y까지의 최소 비용은 모든 이웃 노드 v에 대해 계산된 c(x, v) + dv(y) 중 최솟값이 됨.
  • 실질적인 중요성 : 벨만-포드 식의 해답은 각 노드 포워딩 테이블의 엔트리를 제공
    • x에서 y까지 최단 경로가 v를 거치는 것이라면 v에 패킷 전달
      = 노드 x의 포워딩 테이블에는 v가 지정되어 있어야함.
  • 실질적인 공헌 : DV 알고리즘에서 일어나는 이웃 간 통신의 형식을 제안한다는 점
• 기본 아이디어 : 그냥 벨만 포드 알고리즘임
  • 벨만-포드 알고리즘은 음의 간선이 있는 다익스트라라고 보면 됨
  • Dx = [Dx(y) : y in N]을 노드 x에서부터 N에 속한 모든 다른 노드 y까지의 비용 추정 값의 벡터라고 하면, DV 알고리즘으로 각 노드x는 다음과 같은 라우팅 정보를 유지
    • 각 이웃 노드 v 중에서 x에 직접 접속된 이웃 노드까지의 비용 c(x，v)
    • 노드 x의 거리 벡터, 즉 x로부터 N에 있는 모든 목적지 y로의 비용 예측값을 포함하는 벡터 Dx= [Dx(y): y in N]
    • 이웃 노드들의 거리 벡터들, 즉 v가 x의 이웃이라고 하면 Dv = [Dv(y)：y in N]
  • 노드 x가 이웃 w에게서 새로운 거리 벡터를 수신하면，x는 w의 거리 벡터를 저장하고 벨만-포드 식을 사용하여 다음처럼 자신의 거리 벡터를 갱신
    Dx(y) = minv{c(x，v) + Dv(y)} (N에 속하는 각 노드 y에 대해)
  • 만약 이 갱신으로 인해 노드 x의 거리 벡터가 변경된다면，노드 x는 이 수정된 거리 벡터를 자신의 이웃들에게 전송 -> 이웃들도 자신의 거리 벡터를 갱신
  • 모든 노드가 거리 벡터를 비동기적으로 교환하는 동작을 계속하다 보면，비용 추정값 Dx(y)는 노드 x에서 노드 y까지의 실제 최소 비용 경로의 비용인 dx(y)로 수렴

거리 벡터 (DV) 알고리즘

• DV 유사 알고리즘은 실제로 인터넷의 RIP，BGP, ISO IDRP, Novell IPX, 최초의 ARPAnet 등을 포함하여 많은 라우팅 알고리즘에서 사용

각 노드 x에서

1 	initialization:
2 		for all destinations y in N:
3 			Dx(y)=c(x, y) /* 만약 y가 이웃이아니라면 c (x,y) = ∞*/
4 		for each neighbor w
5 			Dw(y) = ? for all destinations y in N
6 		for each neighbor w
7		send distance vector Dx = [Dx(y) : y in N] to w
8
9	 loop
		/*각 노드는 이웃으로부터의 갱신을 기다림*/
10 		wait (until I see a link cost change to some neighbor w or
11 			until I receive a distance vector from some neighbor w
12
	/* 각 목적지 y에 대해 x는 v*(y)를 결정하고 y에 대해 포워딩 테이블도 갱신*/
13 		for each y in N:
			/* 업데이터를 수신하면 새로 거리 벡터를 계산*/
14 			Dx(y) = minv(c (xz v) + Dv (y) ) /*최솟값을 갖게하는 이웃v*/
15	/*  새로운 거리 벡터를 이웃들에게 배포 */
16 	if Dx(y) changed for any destination y
17 		send distance vector Dx=[Dx (y): y in N] to all neighbors
18
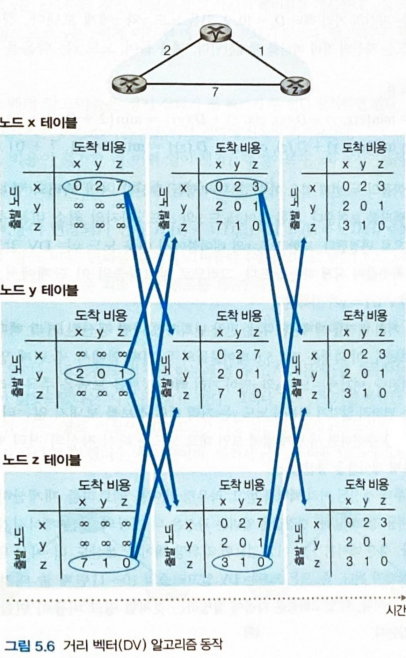
19 	forever

• 그림 5.6 : 세 노드로 이루어진 단순한 네트워크에서의 DV ALG의 동작
  • 알고리즘의 동작은 동기적 방식이다. 즉，모든 노드가 동시에 이웃에게서 거리 벡터를 받고，새로운 거리 벡터를 계산해서 변화가 있다면 그들의 이웃에게 알림
  • 이웃으로부터 갱신된 거리 벡터 수신 -> 라우팅 테이블 엔트리를 재계산 -> 목적지까지 최소 비용 경로의 비용 변경값을 알리기
  • 위 과정을 더 이상의 갱신 메시지가 없을 때까지 계속
  • 갱신 메시지가 없으면, 라우팅 테이블 계산도 없고 알고리즘은 정지 상태
  • ㄴ= 즉，모든 노드는 DV 알고리즘의 10〜11 번째 줄 대기 명령을 수행
    

거리 벡터(DV) 알고리즘: 링크 비용 변경과 링크 고장

• 그림 5.7(a) : y에서 x로의 링크 비용이 4에서 1로 감소한 상황
  • 거리 벡터 알고리즘은 정지 상태가 될 때까지 두 번만 반복하면 됨.
    • t0 : y가 링크 비용이 4->1 감지 -> 자기 거리 벡터 갱신 -> 이웃에게 알림
    • t1 : z는 y로부터 갱신 정보 수신 -> 자기 거리 벡터 갱신 -> 이웃에게 알림
    • t2 : y는 z로부터 갱신 정보 수신 -> 자기 거리 벡터 갱신 -> 정지 상태
  • 비용이 감소한다는 소식은 신속히 퍼짐
• 그림 5.7(b) :y에서 x로의 링그 비용이 4에서 60으로 증가한 상황
  • 1. 링크 비용이 변경되기 전 : Dy(x)=4, Dy(z)=1, Dz(y)=1，Dz(x)=5
    • t0 : y가 링크 비용이 4->1 감지
      • ㄴ> 자기 거리 벡터 갱신
        Dy(x) = min{c(y, x) + Dx(x), c(y，z) + Dz(x)} = min{60 + 0, 1 + 5| = 6
      • 이때 우리는 z 경유하는 비용이 잘못된 것 알지만 가장 최근에 y에게 x에 도착하려면 5의 비용이 필요하다 말했던 사실 뿐이라 y는 모름
    • t1 : x로 가기 위해 y는 z로 경로 설정을 하고，z는 y로 경로 설정을 하는 라우팅 루프 발생 -> 영원히(또는 포워딩 테이블이 변할 때까지) 왔다 갔다 돌아버림
  • 2. t1 : z에게 새로운 거리 벡터를 알림
  • 3. t1 쪼굼 이후 : z 거리 벡터 받음 -> y->x 최소 비용이 6임을 알게됨
       -> z는 y에 도달하기 위해 비용 1 이 필요하다는 사실을 알고 있으므로 x로의 새로운 최소 비용 Dz(x)= min{50 + 0, 1 + 6} = 7을 계산 -> x까지의 최소 비용이 증가 = t2 시각에 새로운 거리 벡터를 y에 알림
  • 4. z의 새로운 거리 벡터 수신 -> y는 Dy(x) = 8을 결정 -> 거리벡터 z에게 전송 -> z는 Dz(x) = 9로 결정 -> 이 거리 벡터를 y에게 전송
  • => z의 y를 통한 경로 비용 계산값이 50보다 커질 때까지 이 루프를 44번 반복(y와 z 간의 메시지 교환)됨 => 링크 비용 증가는 천천히 알려짐
  • 만약 4에서 60이 아니라 10000이면? -> ㅈ댐 = 무한 계수 문제(count-to-infinity problem)

거리 벡터 알고리즘: 포이즌 리버스 추가

• 라우팅 루프를 포이즌 리버스(poisoned reverse)라는 방법을 사용해 방지
  • 만약 z가 y를 통해 목적지 x로가는 경로 설정을 했다면，z는 y에게 x까지의 거리가 무한대라고 알림
  • z는 y를 통과해서 x로 가는 동안은 이러한 거짓말을 계속함. -> y는 z를 통해 x로 가는 경로 시도X
• 하지만 모든 무한 계수 문제 해결X
  -（단순히 직접 이웃한 2개의 노드가 아닌）3개 이상의 노드를 포함한 루프는 포이즌 리버스로는 감지 불가

링크 상태 알고리즘과 거리 벡터 라우팅 알고리즘의 비교

• DV와 LS 알고리즘은 경로를 계산할 때 서로 대비되는 방법을 취함
  • DV 알고리즘 : 각 노드는 오직 직접 연결된 이웃과만 메시지를 교환하지만，자신으로부터 네트워크 내 모든 노드로의 최소 비용 추정값을 이웃들에게 제공
  • LS 알고리즘 : 전체 정보를 필요로 함 -> 모든 라우터에 LS 알고리즘이 구현되면，각 노드는 브로드캐스트를 통해 통신하지만，오직 자신에 직접 연결된 링크의 비용만 알린다.

LS과 DV 알고리즘 속성 비교

• 각각 장단점을 가지기에 뭐가 더 낫다고 말할 순 없음 -> 둘다 잘 쓰고있음
• 메시지 복잡성
  • 링크 상태 알고리즘
    • 각 노드는 모든 링크 비용을 알아야 함 -> O(|N||E|）개의 메시지가 전송
    • 링크 비용이 변할 때마다 새로운 링크 비용이 모든 노드에게 전달되어야 함.
  • 거리 벡터 알고리즘
    • 매번 반복마다 직접 연결된 이웃끼리 메시지를 교환
    • 알고리즘의 결과가 수렴하는 데 걸리는 시간은 많은 요소에 좌우됨
    • 링크 비용이 변할 때, 어떤 노드의 최소 비용 경로에 변화를 준 경우에만 수정된 링크 비용 전파
• 수렴 속도
  • 링크 상태 알고리즘
    • O(|N||E|）개의 메시지를 필요로하는 O(|N|^2）알고리즘
  • 거리 벡터 알고리즘
    • 천천히 수렴하고 알고리즘이 수렴하는 동안 라우팅 루프가 발생 or 무한 계수 문제 발생 가능
• 견고성 : 만약 라우터가 고장나거나 오동작하거나 파손된다면?
  • 링크 상태 알고리즘
    • 라우터는 연결된 링크에 대해 잘못된 비용 정보를 브로드캐스트할 가능성O
    • 노드는 링크 상태 브로드캐스트를 통해 받은 패킷을 변질시키거나 폐기할 가능성O
    • BUT 각 링크 상태 노드는 자신의 포워딩 테이블만 계산
      ㄴ-> 경로 계산 = 어느 정도 분산 수행
      ㄴ=> 어느 정도의 견고성 O
  • 거리 벡터 알고리즘
    • 한 노드의 잘못된 계산은 전체로 획산될 가능성O = ㅈ댐
    • 각 반복마다 한 노드의 거리 벡터 계산이 이웃에게 전달
      -> 다음 반복에서 이웃의 이웃에게 간접적으로 전달하기 때문