📖 그래프 심화 (Graph)

📌 위상정렬 (Topological Sorting)

✅ 위상 정렬이란

• 순서가 있는 작업을 차례로 진행해야 할 때 순서를 결정해 주기 위해 사용하는 알고리즘

• 사이클이 없는 방향 그래프의 모든 노드를 주어진 방향성에 어긋나지 않게 순서를 나열하는 것

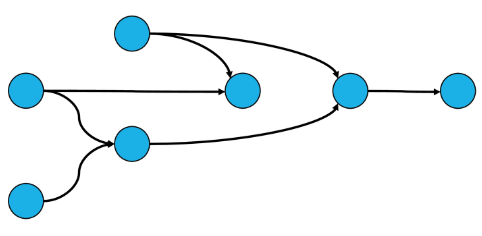
✅ DAG (Directed Acyclic Graph : 유향 비사이클 그래프)

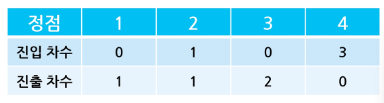
• 진입 차수 (in-degree) : 특정 노드로 들어오는 간선 개수

• 진출 차수 (out-degree) : 특정 노드에서 나가는 간선의 개수

📌 위상정렬 - Queue 구현

✅ Queue를 활용한 위상 정렬 방법

1. 진입 차수가 0인 모든 노드를 Queue에 삽입

2. Queue가 공백 상태가 될 때까지 반복 수행

   2-1> Queue에서 공백상태가 될 때까지 반복 수행 (연결된 노드의 진입 차수를 감소 시킨다.)
   2-2> 새롭게 진입 차수가 0이 된 노드를 Queue에 삽입한다.

• Queue에서 꺼내지는 순서(Queue 들어온 순서)가 위상 정렬을 수행한 결과이다.

✅ Queue를 활용한 위상 정렬 - pseudo code

// G : 인접리스트
// in_degree : 진입차수 저장배열
// Q : 큐

Topological_sort() {
	Q <- indegree가 0인 노드 삽입
    while(!Q_isEmpty) {
    	node = deQueue
        for v in G[node] {
        	in_degree[v] -= -1
            
            if(in_degree[v] == 0)
            	enQueue(v)
        }
    }
}

📌 위상정렬 - Stack 구현

✅ Stack을 활용한 위상정렬 방법

1. 진입 차수가 0인 모든 노드에서 DFS 탐색 수행

2. DFS 수행
   `
   2-1) 해당 노드를 방문 표시
   2-2) 인접하면서 방문하지 않은 노드가 있다면 DFS 재귀 호출
   2-3) 함수 리턴 하기 전 Stack에 현재 노드 저장

3. Stack이 공백 상태가 될 때까지 pop

• Stack에서 꺼내지는 순서를 뒤집으면 위상 정렬을 수행한 결과이다.

✅ Stack을 활용한 위상정렬 - pseudo code

// G : 인접리스트
// in_degree : 진입차수 저장배열
// Stack : 스택
// visited : 방문배열

Topological_sort(v) { // v : 노드
	visited[v] = True
    for u in G[v] {
    	if(visited[u] == False)
        	Topological_sort(u)
    }
    Stack.push(v)
}

for i in 노드번호 {
	if (in_degree[i] == 0) {
    	Topological_sort(i)
    }
}

✅ 위상 정렬 특징

1. 모든 정점을 방문하기 전에 Queue가 공백 상태가 되면 사이클이 존재하는 것 (사이클이 존재하면 진입 차수가 0이 될 수 없다.)

2. 그래프의 유형은 DAG

3. 여러 해답이 존재할 수 있다. (진입 차수가 0인 값이 동시에 생성이 된다면 작성한 코드 방법에 따라 답이 달라진다.)

4. 시간 복잡도 O(V+E)