백준 2003번

수 들의 합 2

문제

N개의 수로 된 수열 A[1], A[2], …, A[N] 이 있다. 이 수열의 i번째 수부터 j번째 수까지의 합 A[i] + A[i+1] + … + A[j-1] + A[j]가 M이 되는 경우의 수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N(1 ≤ N ≤ 10,000), M(1 ≤ M ≤ 300,000,000)이 주어진다. 다음 줄에는 A[1], A[2], …, A[N]이 공백으로 분리되어 주어진다. 각각의 A[x]는 30,000을 넘지 않는 자연수이다.

출력

첫째 줄에 경우의 수를 출력한다.

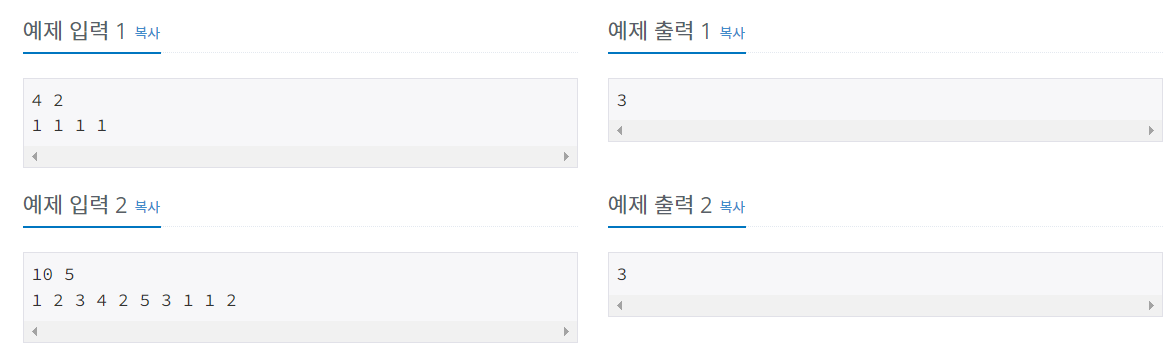
예제

알고리즘 분류

• 두포인터

코드

import java.util.*;
import java.io.*;

public class Main {	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine(), " ");
		
		int N = Integer.parseInt(st.nextToken());
		int M = Integer.parseInt(st.nextToken());
		
		st = new StringTokenizer(br.readLine(), " ");
		int arr[] = new int[N];
		
		for(int i=0; i<N; i++)
			arr[i] = Integer.parseInt(st.nextToken());
		
		System.out.println(Func(arr, M));
	}
	
	public static int Func(int[] arr, int M) {
		int count = 0;
		int startPoint = 0, endPoint = 0;
		int len = arr.length;
		int sum = 0;
		
		while(true) {
			if(sum >= M)
				sum -= arr[startPoint++];
			else if(endPoint >= len)
				break;
			else
				sum += arr[endPoint++];
			
			if(sum == M)
				count++;
		}
		
		return count;
	}
}

풀이

이 문제는 투 포인터 알고리즘을 활용한다.
구간 중 첫 부분을 포인터로 두고, 구간의 마지막 부분도 포인터로 둔다.
두 포인터를 조절하면서 조건을 맞추는 구간의 개수를 센다.
이 때 조건을 맞추기 위해 여러 장치가 필요하다.

이 부분은 다른 블로그에 깔끔하게 정리되어 있어서 큰 도움을 얻었다.
출처 : https://maivve.tistory.com/223

S는 시작점 포인터, E는 끝점포인터이다.
이 방식을 활용하면 시간복잡도 또한 최대 O(N)까지 줄일 수 있다.