✏️ 확률분포 내용까지 공부해서 다시 정리하기
In a parametric model, you know which model exactly you will fit to the data, e.g., linear regression line. In a non-parametric model, however, the data tells you what the 'regression' should look like.
Let me give some concrete examples.
Parametric Model: 𝑦𝑖=𝛽0+𝛽1𝑥𝑖+𝑒𝑖
Here you know what the regression will look like: a linear line.
Non-Parametric Model: 𝑦𝑖=𝑓(𝑥𝑖)+𝑒𝑖
where f(.) can be any function. The data will decide what the function f looks like. Data will not tell you the analytic expression for f(.), but it will give you its graph given your data set.
The reason why people say that there is inherently no difference between parametric and non-parametric regression is that the function f(.) can be perfectly approximated by an infinite-parameter model, which is parametric.
People mostly prefer parametric models because it is easier to estimate a parametric model, easier to do predictions, a story can be told according to a parametric model (e.g., if X goes up by 1 unit then Y will go up by 𝛽
units etc.), and the estimates have better statistical properties compared to those of non-parametric regression.
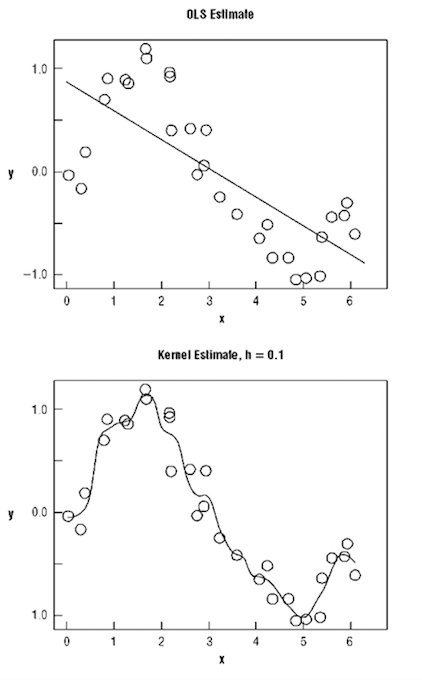
Here is a picture where both parametric and non-parametric regression results are shown. OLS (linear regression line) predicts a negative relationship between X and Y. Nonparametric estimation fits a 'highly wiggly' function to the data (most of the times you can choose the smoothness of the function).