Paper : https://arxiv.org/abs/2303.03755
Github : https://github.com/wix-incubator/DLT

💡 로 표시된 부분은 제가 이해한 내용을 적은 부분입니다. 오류가 있다면 댓글로 남겨주세요 🙏🏻

Abstract

시각적 레이아웃 생성은 그래픽 디자인의 중요한 구성 요소다. 구성 요소 속성의 부분 집합에 레이아웃 생성을 조건부로 할 수 있는 기능은 사용자 상호 작용이 포함된 실제 애플리케이션에서 매우 중요하다.

최근에는 diffusion 모델이 다양한 영역에서 고품질의 생성 성능을 보여 주었다. 그러나 이산(클래스) 및 연속(위치, 크기) 속성의 혼합으로 이루어진 레이아웃의 자연적 표현에 diffusion 모델을 적용하는 방법은 불명확하다.

조건부 레이아웃 생성 문제에 대처하기 위해, 본 논문에서는 DLT라는 joint discrete-continuous diffusion model을 소개한다. DLT는 transformer-based 모델로, 모든 레이아웃 구성 요소 클래스, 위치 및 크기의 임의의 하위 집합에 대한 조건부를 가능하게 하는 유연한 conditioning 메커니즘을 갖추고 있다.

본 논문의 방법은 다양한 레이아웃 생성 데이터셋에서 다양한 메트릭과 조건 설정에 따라 최신의 생성 모델을 능가한다. 또한, 제안한 conditioning 메커니즘과 joint continuous-diffusion 프로세스의 효과를 검증한다. 이 joint 프로세스는 다양한 범위의 혼합 discrete-continuous generative 테스크에 효과적으로 적용될 수 있다.

1. Introduction

---

그래픽 디자인의 중요한 측면은 레이아웃 생성이다. 캔버스나 문서에 시각적 구성 요소를 배열하고 크기를 조절하는 것이다. 잘 설계된 레이아웃은 사용자가 제시된 정보를 쉽게 이해하고 효율적으로 상호 작용할 수 있도록 한다.

고품질의 레이아웃을 생성하는 능력은 모바일 앱 및 웹 사이트의 사용자 인터페이스, 정보 슬라이드를 위한 그래픽 디자인, 잡지, 과학 논문, 인포그래픽, 실내 장면 등 다양한 응용 분야에서 필수적이다.

이를 위해, 생성적 적대 신경망(GANs), 변이형 오토인코더(VAEs), masking completion과 같은 모델링 접근 방식이 새로운 레이아웃을 생성하기 위해 탐구되었다.

이러한 접근 방식은 Recurrent Neural Networks (RNNs) 및 Graph Neural Networks (GNNs)과 같은 다양한 아키텍처를 사용한다. 최근에 제안된 Transformer 기반 접근 방식은 다양한 응용 프로그램 및 사용자 요구 사항에 대한 다양하고 신뢰할 수 있는 레이아웃을 생성하는 데 효과적이다.

레이아웃은 종종 여러 속성으로 구성된 구성 요소의 집합으로 나타낸다. 이는 클래스, 위치 및 크기와 같은 여러 속성으로 구성된다.

NLP의 최근 발전에 따라, 일반적인 방법은

• 구성 요소를 discrete attribute tokens의 시퀀스로 모델링하고

• 모든 속성 토큰을 연결한 것으로 레이아웃을 모델링하는 것이다.

모델은 출력 시퀀스를 생성하기 위해 self-supervised objective (다음 단어 완성 또는 unmasking)을 사용하여 훈련된다.

Discretization process는 위치 및 크기와 같은 기하 속성을 구간으로 나누는 과정이다. 그러나 이산 토큰을 사용하면 (기하학) 데이터의 자연적 표현, 즉 연속적인 데이터를 고려하지 못하며, 이는 레이아웃 구성의 해상도가 낮거나 더 작은 데이터셋에서 잘 표현되지 않는 큰 sparse vocabulary로 이어질 수 있다.

사용자 상호 작용이 필요한 많은 실제 그래픽 디자인 응용 프로그램에 대한 제어 가능한 레이아웃 생성을 제공하는 것이 중요하다.

• 사용자가 구성 요소 클래스 또는 일부 구성 요소와 같은 특정 구성 요소 속성을 고정하고

• 나머지 속성 (위치 및 크기) 또는 구성 요소를 생성할 수 있도록 하려고 한다.

반복 기반 masking completion 접근 방식에서 이러한 조건이 추론 중에만 수행되는데, 이는 모델에게 반복적인 개선 과정 중에 조건이 부분적으로 주어진 부분과 생성된 부분을 구분할 수 있는 능력을 제공하지 않는다. 이러한 분리의 부족은 생성 프로세스에서 모호성을 야기할 수 있으며, 결과적으로 최적의 성능을 발휘하지 못할 수 있다.

Diffusion 모델은 최근에 상당한 관심을 받은 생성적 접근 방식이다. 연속적인 diffusion 모델은 텍스트에서 이미지로의 변환, 비디오 생성, 오디오와 같은 다양한 작업 및 도메인에서 놀라운 생성 능력을 보여 주었다.

Diffusion 모델이 이산 공간으로 확장되었음에도 불구하고, 여전히 연속적이고 이산적 특징으로 구성된 표현을 가진 생성 작업에 이러한 모델을 적용하는 방법에 대한 도전이 남아 있다.

본 논문에서는 레이아웃 생성 및 유연한 편집을 위한 Diffusion Layout Transformer (DLT)를 소개한다.

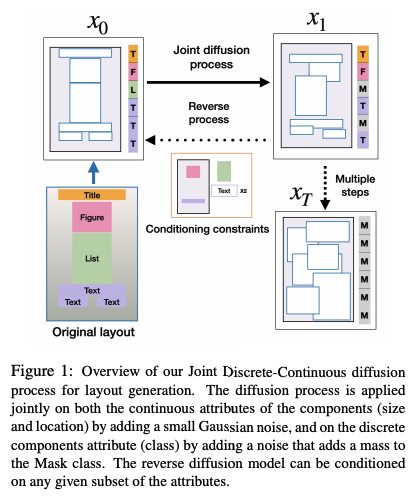
전통적인 diffusion 모델과는 달리, 연속-이산 결합 diffusion 프로세스에 기반한 새로운 프레임워크를 제안하고 유도된 최적화 목적에 대한 이론적 근거를 제시한다.

트랜스포머-인코더 아키텍처를 사용하여, 레이아웃 구성 요소의 연속적인 속성 (크기 및 위치)과 이산적인 속성 (클래스)에 대해 diffusion 프로세스를 함께 적용한다.

모델은 레이아웃의 이산적 표현에 의존하는 트랜스포머 기반 모델의 중요한 한계를 해결한다. 이는 레이아웃 구성의 해상도가 낮아지고 레이아웃 구성의 다양성이 제한될 수 있다.

본 논문의 프레임워크는 유연한 레이아웃 편집을 제공한다. 이는 제공된 레이아웃 구성 요소의 속성 (클래스, 크기 및 위치) 중 임의의 하위 집합에 조건을 걸 수 있도록 한다.

마스킹 완성 접근 방식과 달리, 추론 중에만 조건이 적용되는 것이 아니라, diffusion 이미지 인페인팅 기술에서 영감을 받아 모델이 레이아웃 조건부 작업을 수행하도록 명시적으로 훈련시킨다.

조건 임베딩을 사용하여 어떤 레이아웃 속성에 diffusion 프로세스를 적용할지 제어한다. 이렇게 하면 모델이 반복적인 개선 과정 중에 조건 부분과 생성 부분을 분리할 수 있다. 실험 결과는 이러한 설계 선택이 추론 기반 조건부보다 모델의 성능을 크게 향상시킨다는 것을 보여준다.

DLT 모델의 효과성을 다양한 그래픽 디자인 작업의 인기 있는 레이아웃 데이터셋을 사용하여 여러 일반적인 메트릭에 대해 평가함으로써 연구한다. 광범위한 실험을 통해 제안된 모델이 레이아웃 합성 및 편집 작업에서 최신의 레이아웃 생성 모델을 능가하는 것을 보여준다. 이때 모델의 런타임 복잡성은 이러한 모델과 동등하다.

다양한 대안을 비교함으로써, joint diffusion 프로세스 와 conditioning 메커니즘이 모델의 강력한 생성 능력에 기여하는 것을 보여준다. 본 논문의 joint discretecontinuous diffusion 프레임워크는 일반적인 설계를 갖고 있으며, 따라서 텍스트+이미지, 텍스트+오디오 등의 다른 도메인에도 적용할 수 있다.

2. Related work

---

Layout synthesis

데이터 기반 생성적 방법을 사용하여 고품질, 현실적이고 다양한 레이아웃을 생성하는 작업은 최근 몇 년간 계속해서 주목받고 있다. 이 문제를 해결하기 위해 여러 생성적 방법이 제안되었다.

• LayoutGAN : Generator를 훈련하여 가우시안/균일 분포를 레이아웃 구성 요소의 위치/카테고리로 매핑하는 것으로, 와이어프레임을 렌더링하고 픽셀 기반 discriminator를 훈련시키는 방식이다.

• LayoutVAE : 두 가지 유형의 변이형 오토인코더를 소개한다. 첫 번째 유형은 구성 요소의 카테고리 수의 분포를 학습하고, 두 번째 유형은 카테고리에 따라 조건을 걸어 구성 요소의 위치와 크기를 예측한다.

최근 NLP의 발전으로, 트랜스포머 기반 언어 모델을 레이아웃 생성 작업을 해결하기 위해 제안했다.

• LayoutTransformer : 표준 트랜스포머 디코더 모델이 사용되어 레이아웃 구성 요소의 속성을 생성하는 데 적용되었으며, 이러한 구성 요소는 사전순으로 정렬된다. 훈련은 이전 구성 요소의 속성을 주어졌을 때 다음 속성을 예측하는 selfsupervised objective으로 수행된다.

• BLT : 양방향 트랜스포머 인코더가 사용되어 레이아웃 구성 요소의 속성을 예측한다. 생성된 레이아웃의 품질을 향상시키기 위해, 가장 낮은 확률의 속성을 다시 마스킹하여 반복적으로 레이아웃 속성을 개선한다.

이전 방법과는 달리, 본 논문의 생성적 방법은 diffusion 프로세스를 기반으로 한다. 이는 다양한 분야에서 강력한 생성 능력을 보여주고 있다.

Layout conditioning

사용자 상호 작용이 필요한 많은 실제 그래픽 디자인 응용 프로그램에 적용 가능하도록 하기 위해, 조절 가능한 레이아웃 생성을 위한 다양한 방법이 제안되었다.

• LayoutGAN++ : Generator와 discriminator를 트랜스포머 기반 아키텍처로 대체하여 LayoutGAN을 개선한다. 잠재 공간에서 비선형 최적화 문제를 정의하고 해결함으로써 레이아웃 생성에 대한 제약 조건을 추가하는 방식을 제안한다.

VAE의 경우,

• Neural design network : 그래프 기반 조건부 VAE 모델을 사용하여 레이아웃 생성을 일련의 상대적인 디자인 속성 집합에 제한하는 방법을 제안했다.

• VTN : 조건부 VAE 접근 방식으로, 조건이 RNN에 의해 사전 분포로 매핑되거나 트랜스포머 인코더에 의해 수행된다.

• BLT : 잠재 공간에서 제한을 가하는 조건부 접근 방식과 달리, 단순히 conditioned component attributes를 unmasking 함으로써 수행된다.

BLT과 유사하게, 본 논문의 접근 방식도 동일한 유연한 조절 가능한 conditioning을 허용하며, 추론 중에 모델은 명시적으로 conditioning attributes에 대한 정보를 받는다. 그러나 훈련 중 조건부 시나리오의 최적화를 수행하는 것을 제안하여 모델의 성능을 향상시킨다.

Diffusion Generative Models

Diffusion 모델은 reverse Markov noising 프로세스를 parameterize하는 신경 생성 모델의 한 종류다. Continuous diffusion의 경우, 샘플에 작은 양의 가우시안 노이즈가 추가된다.

Continuous diffusion 모델은 텍스트에서 이미지로의 변환, 비디오 생성, 텍스트에서 3D로의 변환, 그리고 오디오와 같은 다양한 작업 및 모달리티에서 강력한 생성 능력을 보여 주었다.

최근에는 트랜스포머 기반 diffusion 모델이 텍스트에서 이미지로의 생성 및 인간의 동작 생성과 같은 다양한 작업에서 최고 수준의 성능을 보여주었다. 이러한 연구를 바탕으로, 본 논문의 diffusion 모델도 트랜스포머-인코더 아키텍처를 기반으로 한다.

Discrete diffusion process

Diffusion 프로세스를 이산적인 경우로 일반화하기 위해, Structured denoising diffusion models in discrete state-spaces는 카테고리의 확률 벡터에 Markov noising 프로세스를 적용하는 것을 제안한다.

이 방법의 효과는 image captioning 테스크에서 나타났으며, 여기서 stationary distribution은 [MASK] 흡수 클래스에 모든 질량을 가지고 있다.

stationary distribution (정적 분포)
: Markov chain의 균형 상태를 나타낸다.

💡 "[MASK] 흡수 클래스에 모든 질량을 가지고 있다"는 것은 마스크로 지정된 특정 클래스가 나타날 확률이 가장 높다는 것을 의미한다.

레이아웃 생성 작업의 자연적인 표현은 연속적인 (크기와 위치) 및 이산적인 (카테고리) 구성 요소 속성을 모두 포함한다.

본 논문의 접근 방식은 이전 방법과 달리 연속적인 또는 이산적인 diffusion 프로세스를 적용하는 대신, joint distribution에 diffusion 프로세스를 적용한다.

3. Method

---

본 논문의 목표는 제약 조건 c에 의존하여 레이아웃을 생성하는 것이다. 레이아웃은 각각의 구성 요소 Bi가 포함된 N개의 구성 요소 집합으로 나타내어진다.

여기서 각 구성 요소 Bi는 레이아웃 내에서 구성 요소의 위치와 크기를 설명하는 바운딩 박스와 구성 요소 클래스로 구성된다.

BLT와 유사하게, 조건은 레이아웃 구성 요소의 모든 위치, 크기 및 클래스의 하위 집합이다. 특히, 무조건적인 레이아웃 생성도 c = ∅로 설정함으로써 지원된다.

💡 c = ∅로 설정함으로써 제약 조건을 적용하지 않고 레이아웃을 생성할 수 있다. 사용자가 특정한 제약이나 조건을 주지 않고 모든 구성 요소의 위치, 크기, 클래스를 자유롭게 생성할 수 있다. 따라서 무제한의 자유도를 가진 레이아웃을 생성할 수 있는 옵션을 제공한다.

3.1. Diffusion model

---

Denoising diffusion probabilistic models의 프레임워크를 따르면, Diffusion 프로세스는 T step {x¯t}_t^T=0으로 모델링된다. 여기서 x¯0 ∼ q(¯x0)는 실제 데이터 분포에서 샘플링되고, 순방향 프로세스는 x¯t+1 ∼ q(¯xt+1|x¯t)에 따라 샘플링된다. 여기서 q(¯xt+1|x¯t)는 미리 정의된 (알려진) 분포다.

Diffusion 모델은 parameterized된 reverse diffusion 프로세스를 다음과 같이 정의한다:

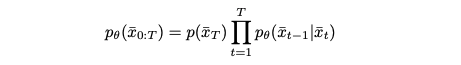
pθ(¯x0)을 실제 데이터 분포 q(x0)와 일치하도록 맞추는 작업은 negative loglikelihood에 대한 variational bound를 최적화함으로써 수행된다.

이 variational bound는 세 가지 항의 합으로 표현될 수 있다:

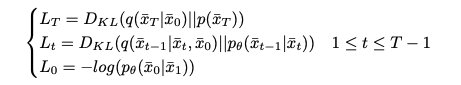
LT가 상수이므로 최적화 프로세스에서 무시할 수 있다.

Continuous diffusion models

연속적인 프로세스에서 함수들은 위첨자 c로 표시한다. 순방향 프로세스는 가우시안 노이즈를 추가함으로써 수행된다.

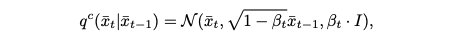
여기서 상수 분산 βt ∈ (0, 1) (초매개변수)가 단계의 크기를 제어한다.

T → ∞일 때, x¯T ∼ N(0, I)를 근사화할 수 있다. 이 경우, pcθ(¯xt−1|x¯t)는 가우시안 분포의 특성을 따르는 모수(parameter)를 사용하여 정의되며, Lct는 닫힌 형식으로 계산할 수 있다.

본 논문의 설정에서, 레이아웃 내의 모든 바운딩 박스에 diffusion 프로세스를 적용한다: x¯0 ∈ R^NX4, 여기서 N은 구성 요소의 최대 수다.

Reverse diffusion 프로세스의 경우, 모델 Fcθ(¯xt, c, y¯t)를 훈련하여 직접 노이즈에서 x¯0을 예측한다. 여기서 y¯t는 다음 단락에 설명된 것처럼 diffusion 프로세스에서 클래스 정보를 전달한다.

최종 손실 Lbox는 손실 Lct의 reweighted 버전으로, 목적을 간소화하고 경험적으로 더 나은 결과를 이끌어 낸다:

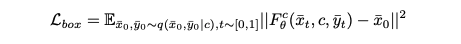
Discrete diffusion models

Discrete 프로세스에서 함수들을 위첨자 d로 표시한다. Discrete diffusion 프로세스는 Structured denoising diffusion models in discrete state-spaces에서 정의되었다.

이 설정에서, K개의 범주를 가진 이산 확률 변수 y0 . . . , yT ∈ {1, . . . , K}가 있다. y0은 데이터 분포에서 샘플링되며, forward noising 프로세스는 Markov transition matrix에 의해 정의된다:

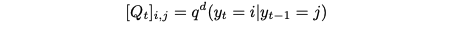
본 논문의 경우, 레이아웃 구성 요소의 모든 클래스에 이산 diffusion 프로세스를 적용한다: y¯0 ∈ {0, .., K}^N. K번째 범주로 absorbing state를 가진 transition matrix를 선택한다.

💡 transition matrix with an absorbing state
: Markov chain에서 특정 상태로 이동한 후 더 이상 다른 상태로 이동할 수 없는 상태를 나타낸다. 이러한 상태를 "흡수 상태" 또는 "흡수 상태로의 이동"이라고도 한다.

따라서 특정 상태로의 이동이 흡수 상태로만 가능한 Markov chain의 transition matrix를 의미한다.

이 경우 i < K일 때:

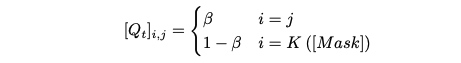
그리고 i = K일 때:

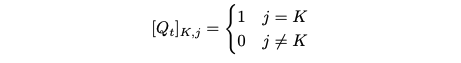
다시 말해, 만약 클래스가 [Mask]이면 동일한 상태로 유지된다. 그렇지 않으면, 확률 β로 클래스가 그대로 유지되고, 확률 1 − β로 [Mask]로 변경된다. T → ∞일 때 y¯T = [Mask]^N을 근사화할 수 있다는 것에 주목해야 한다.

Reverse diffusion 프로세스에서는, 모델 Fdθ(¯xt, c, y¯t)를 훈련하여 구성 요소의 클래스 확률 P˜θ(˜y0|y¯t, x¯t, c)를 직접 예측한다. Reverse diffusion probability의 parameterization은 forward process를 사용하여 정의된다:

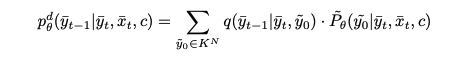
이 경우, 일반적인 교차 엔트로피 손실은 Ldt의 reweighted function이다:

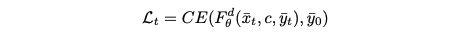
Class category에 대한 objective은 다음과 같다:

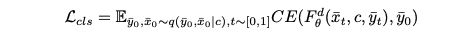
Combined diffusion process

Layout diffusion process는 데이터 분포에서 (¯x0, y¯0)를 샘플링하여 얻는다. forward diffusion 프로세스는 x¯0, y¯0에 독립적으로 연속 프로세스 qc와 이산 프로세스 qd를 적용하여 얻는다.

모델은 결합된 목적 함수로 훈련된다:

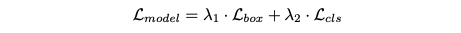
결합된 손실의 이론적 동기는 reverse process의 joint distribution을 이전 단계에 대해 독립적으로 parameterizing함으로써 설명된다:

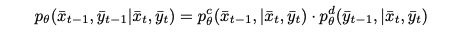
이 분해에서, 연속 부분과 이산 부분의 확률은 여전히 이전 diffusion 단계의 연속 좌표와 이산 클래스에 모두 의존한다.

이러한 매개변수화를 통해 독립적인 분포에 대한 KL-divergence의 가벼운 특성으로 인해 다음과 같이 얻을 수 있다:

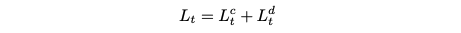
따라서 최종 손실은 joint distribution negative log-likelihood 함수의 간소화된 reweight optimization이다.

Sampling

추론 단계에서는 x¯0 ∼ N(0, I), y¯0 = [Mask]^N을 샘플링한다. 각 단계 t에서는 Fcθ(¯xt, c, y¯t), Fdθ(¯xt, c, y¯t)를 적용하여 x¯pred, y¯pred를 얻는다(여기서 클래스 예측은 확률 벡터로 유지된다).

그런 다음 노이즈를 적용하고 다음과 같이 샘플링한다:

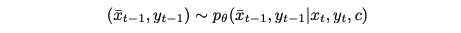
3.2. Model

---

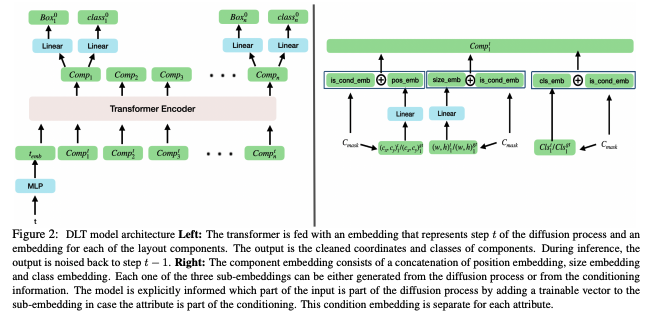
Fθ의 기본은 다층 Transformer 인코더다.

Transformer 네트워크의 입력

: 구성 요소의 임베딩 벡터 세트와 프로세스의 시간 단계 t를 인코딩하는 임베딩

• 시간 임베딩은 MLP 네트워크의 결과로, 시간을 Transformer 임베딩 차원으로 주입한다.

Transformer 인코더의 출력

: 각 구성 요소에 대한 임베딩

• 이는 상자 헤드와 클래스 헤드로 전달된다.

• 상자 헤드는 상자 좌표를 직접 예측하고, 클래스 헤드는 클래스 로짓을 예측한다.

• 클래스 임베딩은 세 가지 다른 임베딩의 연결로 구성된다.

  • 위치 임베딩

  • 크기 임베딩

    • 위치 및 크기 임베딩은 각각 구성 요소의 중심과 크기를 가져와 Linear 레이어로 구현된다.

  • 클래스 임베딩

    • 클래스 임베딩은 각 클래스에 대한 별도의 임베딩 벡터를 보유하는 임베딩 레이어로 구현된다.

3.3. Conditioning Mechanisms

---

레이아웃 편집을 유연한 conditioning 아키텍처를 사용하여 제안한다. 이 아키텍처는 사용자가 conditioning의 일부로 지정되는 특정 레이아웃 정보를 선택할 수 있는 기능을 제공한다. 이는 BLT와 유사한 기능이다.

초기 diffusion image-inpainting 작업을 따라, BLT에서의 편집 과정은 추론 단계에서만 수행되며 알려진 정보를 reverse diffusion 과정에서 노이즈로 대체함으로써 이루어진다. 그러나 최근 diffusion image-inpainting 분야의 발전을 바탕으로, 명시적으로 모델을 레이아웃 편집을 수행하도록 훈련시킨다.

Condition 임베딩(이진 임베딩 레이어로 구현)을 추가하여 편집을 수행하는데, 이는 모델에게 입력 중 어느 부분이 condition되었는지와 diffusion 프로세스의 일부인지를 알려준다.

훈련 중에는 모든 구성 요소의 위치, 크기 및 클래스 중 무작위 하위 집합에 대해 condition을 부여한다. 본 논문에서는 손실을 unconditioned information에만 적용한다.

4.7. Results

---

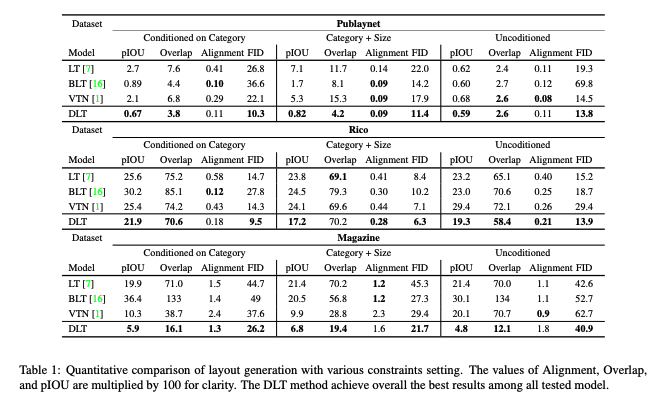
각 모델은 네 번의 시험을 거쳤다. Table 1에서 메트릭의 평균 결과를 보고한다. BLT 모델은 조건부 시나리오에서 LT 모델보다 더 잘 수행되지만, LT 모델은 무조건적인 설정에서 더 나은 성능을 보인다.

그러나 본 논문의 모델은 모든 테스트된 메트릭에 대해 두 시나리오 모두에서 테스트된 방법을 통계적으로 유의한 마진으로 능가한다.

유일한 예외는 일부 경우에 BLT 모델이 더 잘 수행되는 정렬 점수다. 이는 바운딩 박스 차원의 이산화에서 작은 bin 수(32) 때문이다. 이 이산화는 생성된 레이아웃의 구성 요소의 해상도를 제한한다.

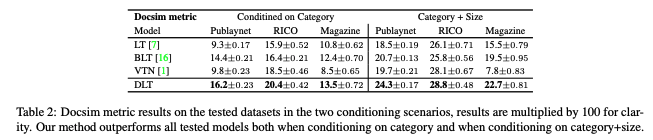
생성된 레이아웃과 조건부 레이아웃 사이의 Docsim 측정 결과는 Table 2에서 확인할 수 있다. 본 논문의 모델은 이 메트릭에 대해서도 조건부 시나리오에서 베이스라인 모델을 능가한다.

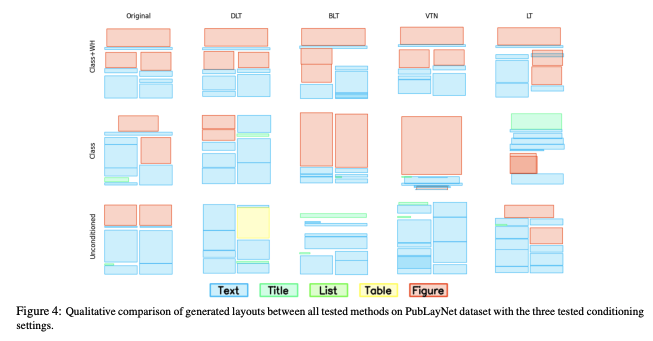
더 나아가, Figure 4는 일반적인 실패 사례를 강조하는 생성된 레이아웃의 질적 비교를 제공한다.

4.8. Key components Analysis

---

제안한 방법의 효과를 조사하기 위해 모델의 주요 구성 요소에 대한 제거 연구를 실시했다.

Conditioning Mechanism

---

3.3에 제시된 조건부 메커니즘을 다음 두 가지 대안과 비교한다:

• 추론 중에만 편집 수행하기
• 조건 임베딩 제거

추론 중에만 편집 수행하기

모델을 무조건적인 설정에 따라 훈련시킨다. 추론 단계에서는 reverse diffusion 과정에서 노이즈를 조건부 정보로 재정의한다. 이 접근 방법(이산 경우)은 BLT의 조건부 접근 방법과 동등하다.

조건 임베딩 제거

여전히 훈련 중에 4.5절에 설명된 세 가지 조건부 설정 중에서 샘플링하되, 약간의 수정으로 구성 요소의 절반에 대한 조건을 추가로 부여한다(무작위 선택). 이 옵션에서 조건 임베딩을 제거한다.

이것은 모델이 입력이 diffusion 프로세스의 일부인지 실제 조건 입력인지에 대한 명시적인 정보를 갖지 않음을 의미한다. DLT 모델은 옵션 (2)에서와 동일한 샘플링으로 훈련되었다.

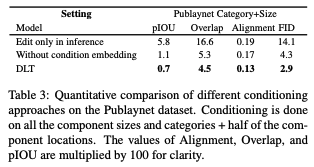
Publaynet 데이터 세트에서 모든 구성 요소의 카테고리 + 크기를 조건으로 하거나 구성 요소의 절반의 모든 정보를 조건으로 하는 경우에 대한 비교는 Table 3에 제공된다. 추론 중에만 조건을 부여하는 것은 모델의 성능을 상당히 저하시켰으며, 조건 임베딩을 추가하면 결과가 더 개선된다. 이 정보(어떤 구성 요소가 조건부인지)는 모델이 조건부 모호성을 해결하고 생성된 구성 요소를 조건부 구성 요소에 맞추는 데 도움이 된다.

Joint Continues-Discrete diffusion process

제안한 연속-이산 결합 diffusion 과정의 효과를 평가하기 위해 두 개의 순차적인 diffusion 과정을 독립적으로 실행하는 것과 비교한다. 첫 번째 비교된 모델에서는 먼저 카테고리에 대한 이산 diffusion 과정을 실행한다.

훈련 중에는 섹션 4.5에서 설명한 무조건적인 설정을 박스 위치와 크기에 대한 조건으로 대체하여 모든 상자의 위치와 크기를 제로로 설정한다. 이렇게 함으로써 모델은 각 샘플마다 이산 프로세스 또는 연속 프로세스 (둘 다가 아닌 하나만)를 반전시키도록 훈련된다.

추론에서는 먼저 구성 요소 카테고리에 대한 이산 diffusion 프로세스를 실행한 다음 예측된 카테고리를 고려하여 이산 diffusion 프로세스 결과에 대한 연속 reverse diffusion 프로세스를 실행한다. 두 번째 비교 방법에서는 먼저 연속 reverse diffusion 프로세스를 실행한 다음 이산 reverse 프로세스를 실행한다.

훈련 중에는 무조건적인 설정을 두 가지 설정으로 대체하여 이를 수행한다.

• 모든 카테고리가 마스크 토큰과 같은 상태로 condition이 지정된 구성 요소 위치 + 크기에서 연속 diffusion 프로세스를 실행한다.

• 구성 요소의 위치 + 크기에 대한 condition으로 이산 diffusion 프로세스를 실행한다. 또한 이 방법에서도 각 샘플에 대해 모델을 이산 diffusion 프로세스 또는 연속 diffusion 프로세스를 반전시키도록 훈련한다.

추론에서는 먼저 모든 카테고리가 마스크 토큰과 같은 상태로 condition이 지정된 연속 역 diffusion 프로세스를 실행하여 구성 요소 위치를 예측한 다음 박스 위치를 조건으로하는 이산 역 diffusion 프로세스를 실행한다.

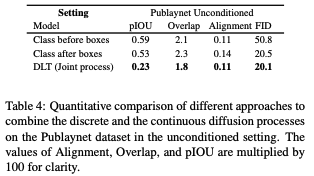
Publaynet 데이터 세트에서 무조건적인 설정에 대한 결과를 Table 4에 제공한다. 제안한 연속-이산 결합 diffusion 프로세스가 순차적인 diffusion 프로세스를 능가한다. 또한 주의할 점은 연결 모델의 추론 시간이 두 배 빠르다는 것이다.

5. Conclusions and future work

---

이 연구에서는 레이아웃 구조의 부분 정보가 주어진 상황에서 합성 레이아웃을 생성하기 위한 새로운 방법을 제안한다. DLT 모델은 레이아웃 구성 요소의 카테고리와 차원에 대해 연속-이산 결합 diffusion 프로세스를 수행하는 Diffusion layout transformer다.

모델은 조건 임베딩을 사용하여 입력에 대한 유연한 조건을 제공하여 어느 구성 요소 부분에 diffusion 프로세스가 적용되는지 명시적으로 지정한다.

세 가지 다른 조건 설정에 대한 세 공개 데이터 세트에서의 실험 결과는 제안한 방법의 효과성과 유연성을 보여주며 기존 방법을 능가한다는 것을 입증한다. 또한 모델의 주요 구성 요소의 효과를 탐구한다.

다양한 대안을 비교함으로써 연속-이산 결합 프로세스와 조건 메커니즘의 추가 가치를 보여준다. 현재 작업의 한계는 구성 요소의 내용을 고려하지 않고 생성 프로세스를 진행한다는 점이다. 이 정보는 생성 프로세스의 많은 모호성을 해소하는 데 매우 중요하며 결과를 크게 개선할 수 있다.

DLT 변환기의 임베딩 입력이 레이아웃 구성 요소를 나타내므로 구성 요소 임베딩에 구성 요소 내용에 대한 더 많은 정보를 인코딩하여 본 논문의 솔루션을 확장하는 것이 자연스럽다. 앞으로 이 방향을 더 탐구할 계획이다.