💛 간략한 PCA(Principal Component Analysis, 주성분분석)

PCA란?
주성분분석이란 여러 개의 반응변수로 얻어진 다변량 데이터에 의해 분산-공분산 구조를 선형결합식(주성분)으로 설명하고자 하는 분석 방법이다. N개의 개체와 p개의 변수를 저차원 그래프에 타점하고, 개체들을 분류하여 특성을 파악한다.

PCA의 목적
차원축소 및 주성분을 통한 데이터 해석

PC란?
모평균 벡터와 모분산행렬을 가진 벡터가 선형결합이나 회전변환을 통해 새로운 좌표축을 형성할 수 있다. 이렇게 생성된 새로운 축은 데이터의 변동을 최대로 설명해주고, 공분산 구조에 대한 해석을 용이하도록 만들어줄 수 있는데 이를 주성분(PC, Principal Component)이라고 한다.

• 제1주성분: 변동을 최대로 설명해주는 방향으로 변수들의 선형 결합식
• 제2주성분: 제1주성분 다음으로 변동을 가장 많이 설명해주는 변수들의 선형결합식이고 제1주성분과 독립(주성분의 기하학적 의미는 서로 직교관계)
  위의 출처, R로 PCA하는 과정을 상세히 설명한 블로그

💛 Scree Plot

Scree Plot: PCA 분석 후 주성분 수를 선정하기 위해 고유값-주성분의 분산 변화를 보는 그래프로, 고유값 변화율이 완만해지는 부분이 필요한 주성분의 수이다. (Scree: 비탈, 자갈을 의미한다.)

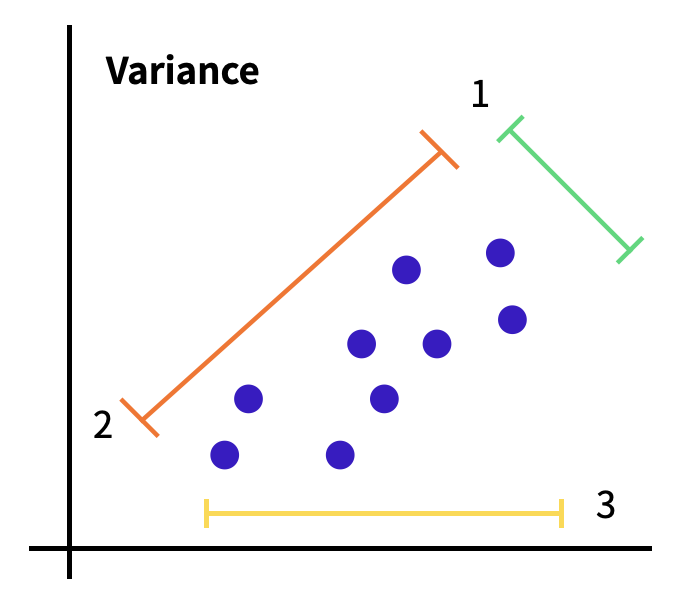
주어진 데이터가 보라색이라면 1번 축, 2번축, 3번 축으로 나누어서 차원축소를할 수 있다. 어떠한 축들로 차원축소를 하는 것이 더 분산이 클 지 확인하여 차원축소를 하는 것이 PCA이다. 그렇다면 어떤 축을 선택하는 것이 좋을 지 선택해야한다. 이를 위한 시각화 중 하나가 스크리 플롯이다.

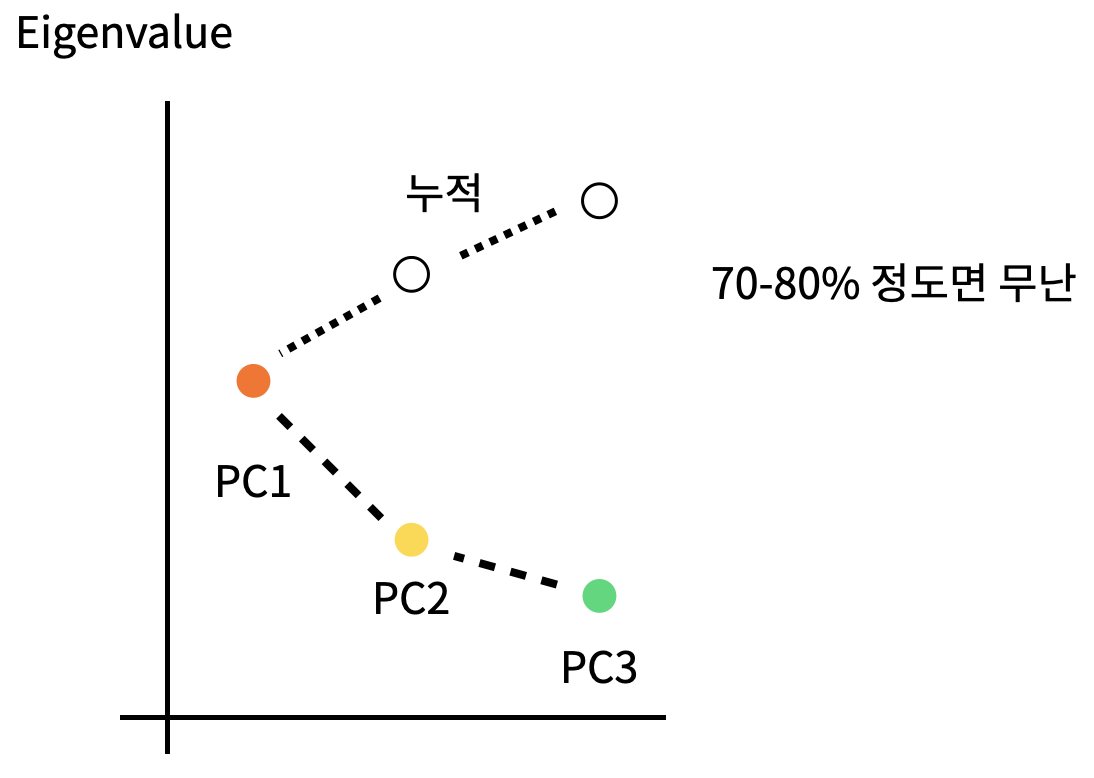
가로축은 PC의 개수, 세로축은 고유값을 선택하는 것이 일반적이었다.
해당 데이터를 몇 퍼센트 정도 설명하고자 하는 지에 따라 누적 퍼센트값을 표시하는 경우도 많았다.

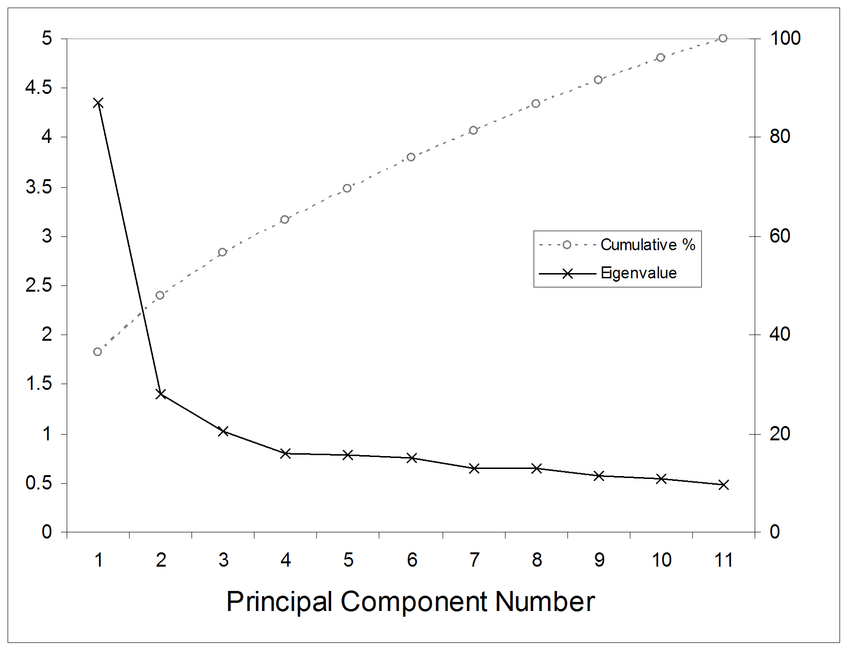
python 예제

#모듈 준비
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
%matplotlib inline
from sklearn.datasets import make_blobs
from sklearn import decomposition

#데이터셋 만들기
X1, Y1 = make_blobs(n_features = 10, n_samples = 100, centers = 4, random_state = 4, cluster_std = 2) 
## random하게 simulation data 생성
#10차원의 센터4개인 데이터로 정하겠다(그룹끼리 얼마나 퍼지는가 설정하는 파라미터)

#PCA를 진행하여 fit한 데이터셋으로 만들어 줌.
pca = decomposition.PCA(n_components = 4)
pc = pca.fit_transform(X1)

#데이터프레임으로 만들어주며 PC로 변환한 값을 만들어준 뒤 cluster라는 새로운 행을 만듦.
pc_df = pd.DataFrame(data = pc, columns = ['PC1', 'PC2', 'PC3', 'PC4'])
pc_df['Cluster'] = Y1
pc_df.head()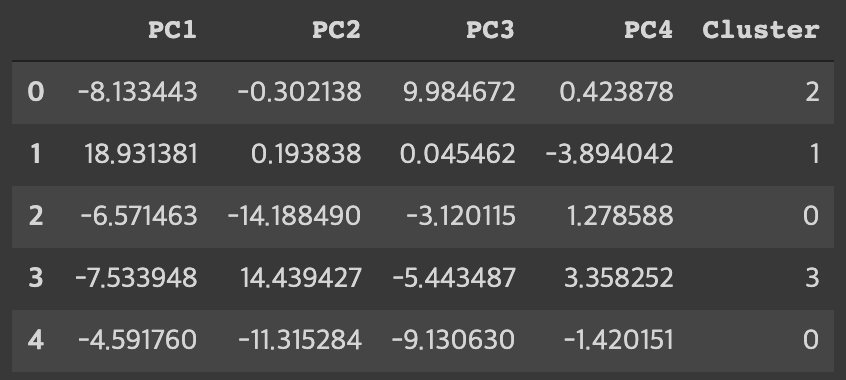

여기서부터 scree plot을 그린다.

def scree_plot(pca):
    num_components = len(pca.explained_variance_ratio_)
    ind = np.arange(num_components)
    vals = pca.explained_variance_ratio_ 
    
    ax = plt.subplot()
    cumvals = np.cumsum(vals)
    ax.bar(ind, vals, color = ['#00da75', '#f1c40f',  '#ff6f15', '#3498db']) # Bar plot
    ax.plot(ind, cumvals, color = '#c0392b') # Line plot 
    
    for i in range(num_components): #라벨링(바 위에 텍스트(annotation) 쓰기)
        ax.annotate(r"%s" % ((str(vals[i]*100)[:3])), (ind[i], vals[i]), va = "bottom", ha = "center", fontsize = 13)
     
    ax.set_xlabel("PC")
    ax.set_ylabel("Variance")
    plt.title('Scree plot')
    
scree_plot(pca)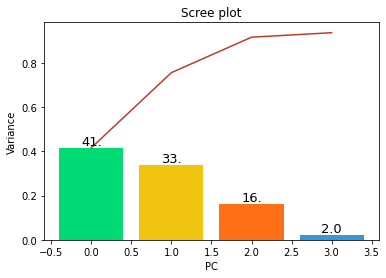

결과값은 위와 같고 10차원의 데이터를 2차원으로 축소했을 때 PC를 3개를 고르면 약 90%를 설명할 수 있다는 해석을 할 수 있다.