내가 만든 예측모델이 정말 적절한지 평가하기 위해서는 문제 상황에 적합한 평가지표를 사용해야하며 특히 분류 모델인지, 회귀 모델인지에 따라 평가지표는 완전히 다르다.

각 예측모델의 평가지표 공식문서

• sklearn에 내장되어 있는 평가지표 : scikit_learn metrics
• 분류(classification) 모델에 쓰이는 평가지표 : classification-metrics
• 회귀(regression) 모델에 쓰이는 평가지표 : regression-metrics

분류문제

분류문제에서 타겟 클래스의 비율이 70% 이상 차이날 경우에는 정확도만 사용하면 적절한 판단을 할 수 없다. '정밀도(precision)','재현율(recall)', 'ROC curve', 'AUC' 등을 같이 사용해야한다.

정밀도, 재현율, 조화평균

# precision, recall, f1-score

from sklearn.metrics import classification_report

y_pred = pipe.predict(X_val)
print(classification_report(y_val, y_pred))

AUC

# AUC score

from sklearn.metrics import roc_auc_score

y_pred_proba = pipe.predict_proba(X_val)[:,-1]
print('AUC score: ',roc_auc_score(y_val, y_pred_proba))

ROC curve

# ROC curve

from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt

plt.scatter(fpr, tpr, color='blue')
plt.plot(fpr, tpr, color='green')
plt.title('ROC curve')
plt.xlabel('FPR')
plt.ylabel('TPR')

불균형 클래스

타겟 특성의 클래스 비율이 차이가 많이 날 경우가 있다.(사실 현업에서는 데이터가 불균형인 경우가 훨씬 많다고 한다.) 데이터의 클래스가 불균형일 경우 예측에 지장을 줄 수 있다. 클래스의 불균형을 맞추는 기술은 적은 범주의 데이터가 유의미할 때 주로 사용된다.

Handling Imbalanced Datasets in Deep Learning
만약 예측 모델로 집을 살지 말지 결정한다면 '집을 산다'가 매우 정확할 경우 '집을 사지 않는다' 클래스에 있는 데이터는 크게 중요하지 않을 것이다. 하지만 '집을 산다'에 해당되는 데이터의 양보다 '집을 사지 않는다.'에 들어갈 데이터가 일반적으로 더 많을 것이기 때문에 내가 만든 모델은 '집을 사지 않는다.' 쪽에 더 편향될 것이다. 왜냐하면 데이터가 상대적으로 적은 '집을 산다' 쪽의 예측이 별로 정확하지 않을 것이기 때문이다.
이를 해결하는 방법 중 하나는 '집을 산다' 쪽의 데이터에 가중치를 두어 예측의 정확도를 높이는 것이 있다.

대부분 scikit-learn 분류기들은 class_weight와 같은 클래스의 밸런스를 맞추는 파라미터를 가지고 있다.

• 데이터가 적은 범주 데이터의 손실을 계산할 때 가중치를 더 곱하여 데이터의 균형을 맞추거나
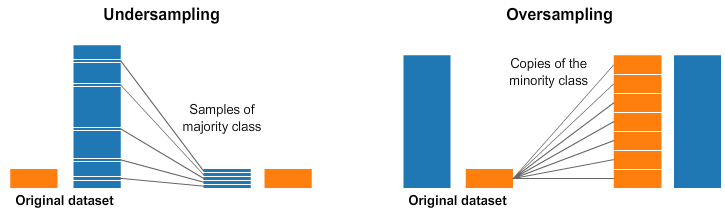
• 적은 범주의 데이터를 추가 샘플링(oversampling)하거나 많은 범주 데이터를 적게 샘플링(undersampling)하는 방법이 있다.

분류 모델 : 범주의 비율 확인하기

class_weight에서 원하는 비율을 적용하거나 class_weight ='balance'옵션을 사용한다.

# 범주의 비율 확인하기

y_train.value_counts(normalize = True)

False와 True에 해당하는 데이터가 전체 데이터의 몇 퍼센트를 차지하는지 나온다.

# class_weights 계산
# n_samples/(n_classes * np.bincount(y))
custom = len(y_train)/(2 * np.bincount(y_train))
custom

False와 True 클래스의 가중치가 array 형식으로 나온다.

# 위의 가중치를 적용한 pipeline 만들기
pipe = make_pipeline( 
	OrdinalEncoder(),
        DecisionTreeClassifier (max_depth = 5, class_weight = {False:custom[0], True:custom[1]}, 
        random_state = 2)
        
pipe.fit(X_train, y_train)
print('검증 정확도: ', pipe.score(X_val, y_val))

위의 분류 문제의 학습 결과를 다양한 평가지표로 확인해보자

# 정밀도, 재현율, f1-score 등을 확인하기

y_pred = pipe.predict(X_val)
print(classification_report(y_val, y_pred)

# AUC score

y_pred_proba = pipe.predict_proba(X_val)[:,-1]
print('AUC score: ',roc_auc_score(y_val,y_pred_proba))

fpr, tpr, thresholds = roc_curve(y_val, y_pred_proba)
plt.scatter(fpr, tpr, color = 'blue')
plt.plot(fpr, tpr, color = 'green')
plt.title('ROC curve')
plt.xlabel('FPR')
plt.ylabel('TPR')

회귀 모델: 타겟의 분포 확인하기

회귀분석에서는 타겟의 분포가 비대칭 형태인지 확인해야한다.

선형 회귀모델은

• 일반적으로 특성과 타겟 간의 선형 관계를 가정한다.
• 특성 변수들과 타겟 변수의 분포가 정규분포 형태일 때 좋은 성능을 보인다.

특히 타겟 변수가 왜곡된 형태의 분포(skewed)일 경우, 예측 성능에 부정적인 영향을 미친다.

# 타겟 분포가 right(positively) skewed 혹은 left(negatively) skewed 되어 있는지 확인하기

sns.displot(target)

타겟이 right-skewed되어 있다면 로그 변환을 사용해보기.
log-transform을 하면 비대칭 분포 형태를 정규분포 형태로 변환시켜준다.

• log1p : ln(1 + x), numpy의 함수로, log(1+x)를 해준다.
• expm1 : exp(x)-1, log1p의 역수이다.

plots = pd.DataFrame()
plots['original'] = target
plots['transformed'] = np.log1p(target)
plots['backToOriginal'] = np.expm1(np.log1p(target))

fig, ax = plt.subplots(1, 3, figsize = (15, 5))

sns.histplot(plots['original'], ax = ax[0]);
sns.histplot(plots['transformed'], ax = ax[1]);
sns.histplot(plots['backToOriginal'], ax = ax[2]);

이렇게 정규분포 형태로 변환을 각각의 훈련, 검증, 테스트 셋에게 해주기

# transformedTargetRegressor
from sklearn.model_selection import train_test_split

df = df[df[target].notna()]

train, val = train_test_split(df, test_size=260, random_state=2)

features = train.drop(columns =[target]).columns

X_train = train[features]
y_train = train[target]
X_val = val[features]
y_val = val[target]

from cateogry_encoders import OrdinalEncoder
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestRegressor
from sklearn.compose import TransformedTargetRegressor

pipe = make_pipeline(
    OrdinalEncoder(),
    SimpleImputer(),
    RandomForestRegressor(random_state = 2)
)

tt = TransformedTargetRegressor(regressor = pipe,
                func = np.log1p, inverse_func = np.expm1)

tt.fit(X_train, y_train)
tt.score(X_val, y_val)