들어가기 앞서, 분산과 표준편차 다시 보기!

분산(variance)이란 데이터가 얼마나 퍼져있는지 측정하는 방법.
각 값의 평균으로부터 차이를 제곱한 것의 평균이다.

분산의 연산 방법
$v$ =$\frac{\sum{(X_{i} - \overline{x})^{2}} }{N}$ = $\sigma^{2}$

이러한 분산은 떨어진 정도를 나타내주지만 데이터의 스케일에도 영향을 받는다.
같은 정도로 퍼져있는 데이터 100개와 같은 정도로 퍼져있는 데이터 20000개의 데이터의 분산의 크기는 차이가 있을 수 밖에 없다.

분산은 각 값들의 평균으로부터 차이의 제곱을 해주기 때문에 거리의 크기 값을 비교할 수 있다. 분산이 크면 클수록 평균에서 멀리 떨어진 것이고 작으면 작을수록 평균에 모여있는 것이다.

분산의 차이는 비교하고자 하는 두 분산을 나눠 비율을 구해준다.

분산을 계산하는 방법은 모집단이냐 샘플이냐에 따라 달라진다. 모집단의 분산 $\sigma^{2}$은 모집단의 parameter(aspect, property, attribute, etc)이며, 샘플의 분산 $s^{2}$은 샘플의 statistic(estimated attribute)이기 때문이다.

샘플의 분산은 모집단의 분산을 예측한 값이다. 일반적으로 샘플의 분산을 계산할 때는 N-1(자유도)로 나누어야 한다. 왜냐하면 샘플의 분산을 구할 때 샘플의 평균을 구해야하니까 그 파라미터의 개수(1)를 빼주기 때문이다. 그냥 n으로 나누게 되면 샘플이 모집단에서 치우쳐져있는 곳에 있었을 경우 그 치우쳐진 값은 모집단의 분산에 큰 영향을 미치는데 그 샘플에서의 분산에는 영향이 작다. 따라서 분모에 n-1을 해주면 n으로 나누었을 때보다 커지므로 과소평가된 샘플의 분산이 커져서 좀 더 모집단의 분산과 가까워질 수 있게 되는 것이다.

---

표준편차(standard deviation)는 분산의 값에 루트를 씌운 것이다. 데이터의 스케일에 영향을 받는 분산에 비해 루트를 씌운 표준편차는 스케일에 대한 영향을 덜 받을 수 있다.

---

⭐️ Covariance (공분산)

Covariance(공분산)이란 1개의 변수 값이 변화할 때 다른 변수가 어떠한 연관성을 나타내며 변할지를 측정하는 것이다.
$cov(x,y)$

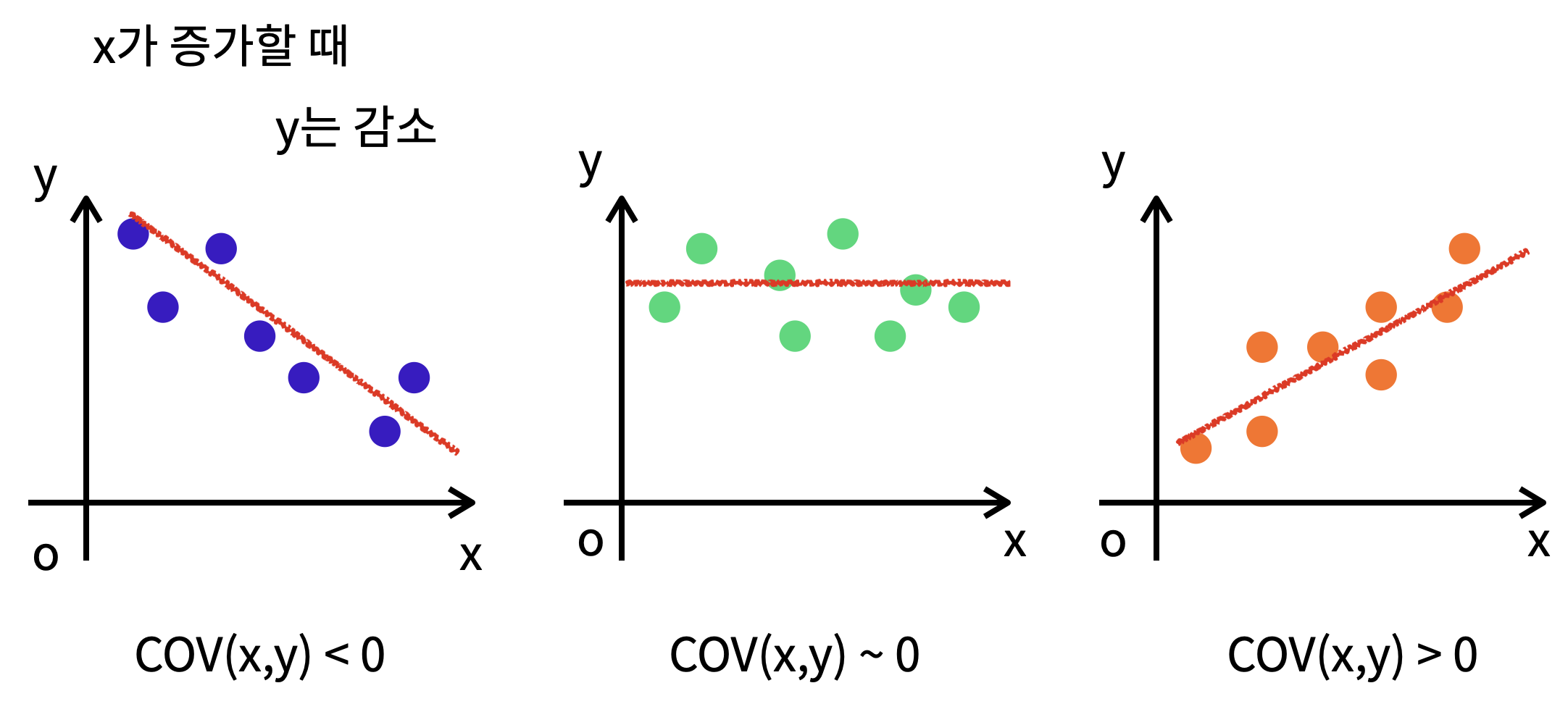
$cov(x,y) < 0$ : y의 값이 높을 때 x의 값이 낮다.
$cov(x,y)과 0이 유사한 값$ : 변수 들의 높고 낮음에 대한 관련성을 알 수 없다.
$cov(x,y) > 0$ : y의 값이 높을 때 x의 값이 높다.

공분산의 값이 크다면 두 변수 간의 연관성이 크다고 해석할 수 있다!
하지만 분산은 데이터의 스케일에 영향을 많이 받기 때문에 값이 크다고해서 무조건 연관성이 크다고 할 수 없다. 연관성이 적더라도 큰 스케일을 가지고 있다면 연관성이 높지만 작은 스케일을 가진 변수들에 비해서 높은 공분산 값을 가지게 된다.

import numpy as np

np.cov(x, y)

>>>[[x,x의 공분산, x,y의 공분산],
 [y,x의 공분산, y,y의 공분산]]

이 때, x,y의 상관계수만을 확인하려면 다음과 같이 입력하면 된다.

np.cov(x, y)[0][1]

⭐️ Correlation coefficient (상관계수)

Correlation coefficient (상관계수)란 공분산의 스케일을 조정하여 -1에서 1까지로 정해진 범위 안에서 양이나 음의 방향으로 선형연관성이 얼마나 큰지에 대한 값을 갖도록 하는 것이다. 상관계수는 numerical한 데이터에 대해서만 적용할 수 있다.
$cor(X,Y)$ = $r$ = ${cov(X,Y)} /{\sigma_{X}\sigma_{Y}}$

여기서 설명하는 상관계수는 numerical한 데이터에 대해서 적용할 수 있다.

😍상관계수의 장점😍
1. 공분산은 이론상 모든 값을 가질 수 있어 비교하기가 어렵지만 상관계수는 -1부터 1까지의 값으로 정해지기 때문에 비교하기 쉽다.
2. 공분산은 항상 스케일과 단위에 영향을 받지만 상관계수는 스케일과 단위에 영향을 거의 받지 않는다.
3. 상관계수는 데이터의 평균 혹은 분산의 크기에 영향을 받지 않는다.

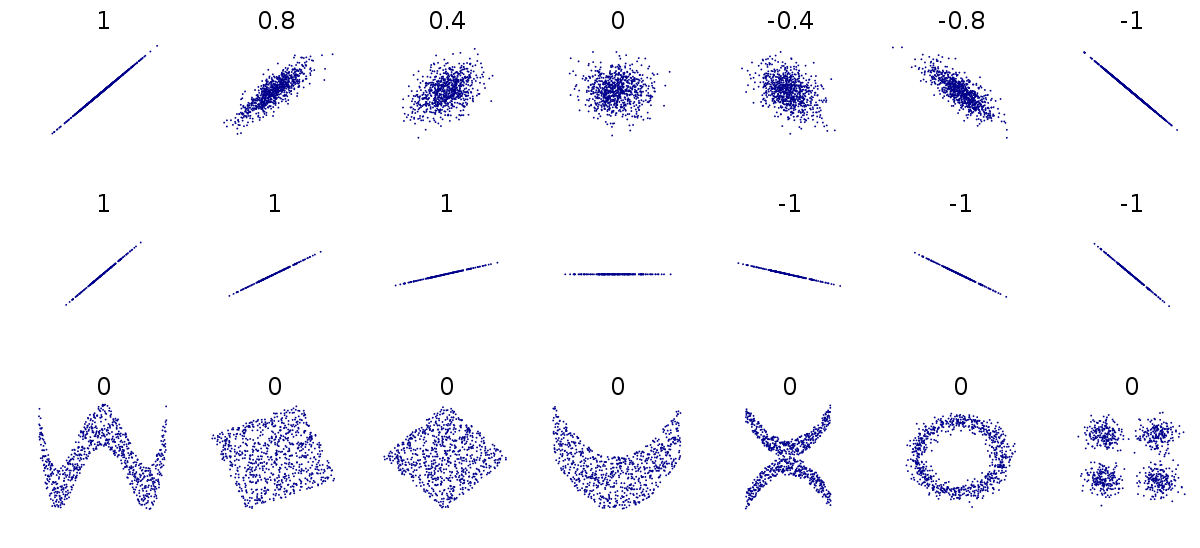
상관계수가 1이다. = 한 변수가 다른 변수에 대해서 완벽한 양의 선형 관계를 가지고 있다.
상관계수가 -1이다. = 한 변수가 다른 변수에 대해서 완벽한 음의 선형 관계를 가지고 있다.
상관계수가 0이다. = 두 변수의 선형연관성이 없다.

import numpy as np

np.corrcoef(x, y)

>>> [[x,x의 상관계수, x,y의 상관계수],
 [y,x의 상관계수, y,y의 상관계수]]

이 때, x,y의 상관계수만을 확인하려면 다음과 같이 입력하면 된다.
순서를 유의해야한다!

np.corrcoef(x, y)[0][1]

❗️ 이 상관계수를 제곱하면 X와 Y분산(=변화량)이 서로 공통되는 부분을 알 수 있다.
: 예를 들어 x와 y의 상관계수가 0.5이면 그 제곱은 0.25이다.
: X의 분산 중 25%를 Y와 공유한다.
: x의 분산 중 25%가 Y로 설명할 수 있다.

Spearman correlation(categorical한 데이터의 상관계수를 구하는 방법)

참고! non-parametric

spearman correlation coefficient는 값들에 대해서 순서 혹은 rank를 매기고, 그를 바탕으로 correlation을 측정하는 non-parametric한 방식이다.

import scipy.stats

scipy.stats.spearmanr(x, y).correlation

⭐️ Orthogonality(데이터의 직교성, 수직성)

Orthogonality(직교성, 수직성)
벡터 혹은 매트릭스가 서로 수직으로 있는 상태

Orthogonality의 의미

• 두 벡터 혹은 매트릭스의 상관관계가 없다.
• 공분산, 상관계수가 모두 0이다.
• 특수한 케이스로 독립성의 부분집합이라고 할 수 있다.
  내적(inner)한 값은 0이다.

+) inner(내적)값이 0인 두 벡터, 혹은 매트릭스는 수직이다. = 상관관계가 없다.

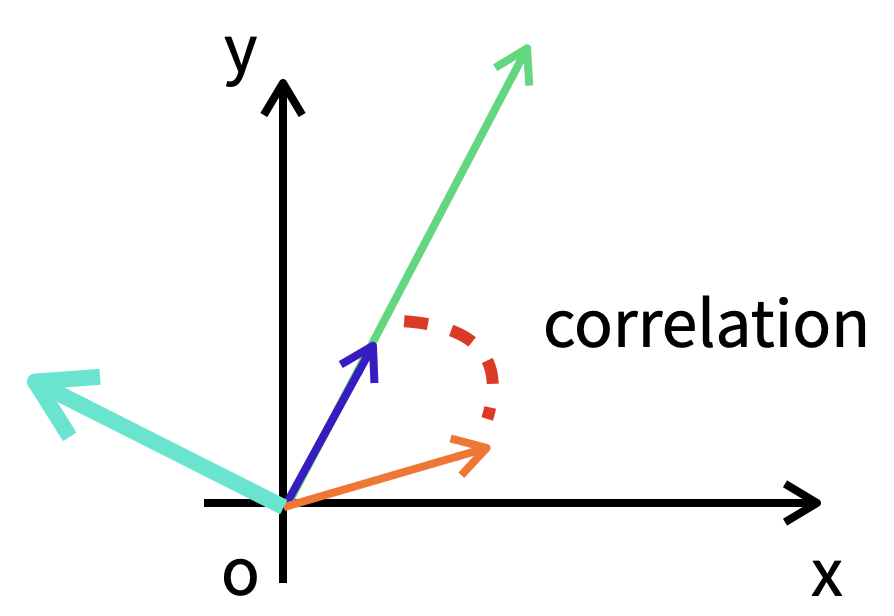
• 하나가 증가할 때, 다른 하나도 증가 하는 경향을 파악하는 것이 공분산이다.
• 단, 수직인 벡터는 다른 벡터와 상관 관계가 전혀 없다.
• 민트색 벡터는 보라색과 연두색 벡터와 수직으로 만나는데 이 둘은 상관관계가 없다. = 독립적인 데이터이다.

선형 관계가 있다 vs 상관 관계가 없다

데이터가 (벡터가) 선형 관계가 있는 것과 상관 관계가 없는 것이 어떤 의미를 가질까?

---

💎 데이터사이언스에서의 활용

좌표 상에 있는 거의 모든 벡터는 다른 벡터와의 상관이 작게라도 있다.
(공분산의 개념을 생각해보자! 하나가 증가하면 다른 하나도 증가하는 경향을 파악하는 것이 공분산이다!)
단, 수직인 벡터만 상관관계가 없다.

❓ 데이터들이 서로 어떤 관계를 갖는지 파악할 수 있는 지표로서 분산, 공분산, 상관계수,직교성을 배운 게 아닐까?

❓ 데이터나 벡터가 선형 관계가 있는 것과 상관 관계가 없는 것은 어떤 의미를 가질까?