프로세서와 메모리 사이에 놓여, CPU에서 고속으로 접근해야 할 데이터를 모아놓은 공간 (SRAM을 사용)
CPU가 Main Memory까지 접근하는 시간이 매우 오래 걸리므로, 최근에 사용된 데이터를 Cache에 저장해 속도를 현저히 줄일 수 있다.
Cache Hit
Cache에 CPU가 요구하는 데이터가 존재하여, Disk I/O를 하지 않고 원하는 데이터를 사용하는 것
Cache Miss
Cache에 CPU가 요구하는 데이터가 없어서 Disk I/O를 하여 원하는 데이터를 사용하는 것
- Miss Penalty
Miss가 난 경우에 데이터를 사용하기까지 걸리는 시간 - Miss Rate
1 - hit ratio,misses / accesses
Access Time = hit time + miss rate * miss penalty
Access Time을 줄이려면 Miss를 최소하해야 한다.
Build Cache
기본적으로 Direct Mapped, Set Associative방법
+ Block Size, Replacement/Write Policy
Cache Design
Direct Mapped
Modulo방식을 사용
Cache[Block % n] = Memory[Block]
Hit rate가 Working Set Size까지는 급격히 증가하지만, 그 이후에는 거의 증가하지 않는다.
Tag, Valid bit가 존재
- Tag
Address의 앞부분(뒷부분은 index)
Tag가 Cache의 Tag와 일치할 때 Cache Access - Valid bit
Cache에 존재하는지 아닌지를 판단하는 bit
Larger Block Size
많이 사용되는 데이터들이 있으므로, 여러 개의 데이터들을 한꺼번에 가져오기 위함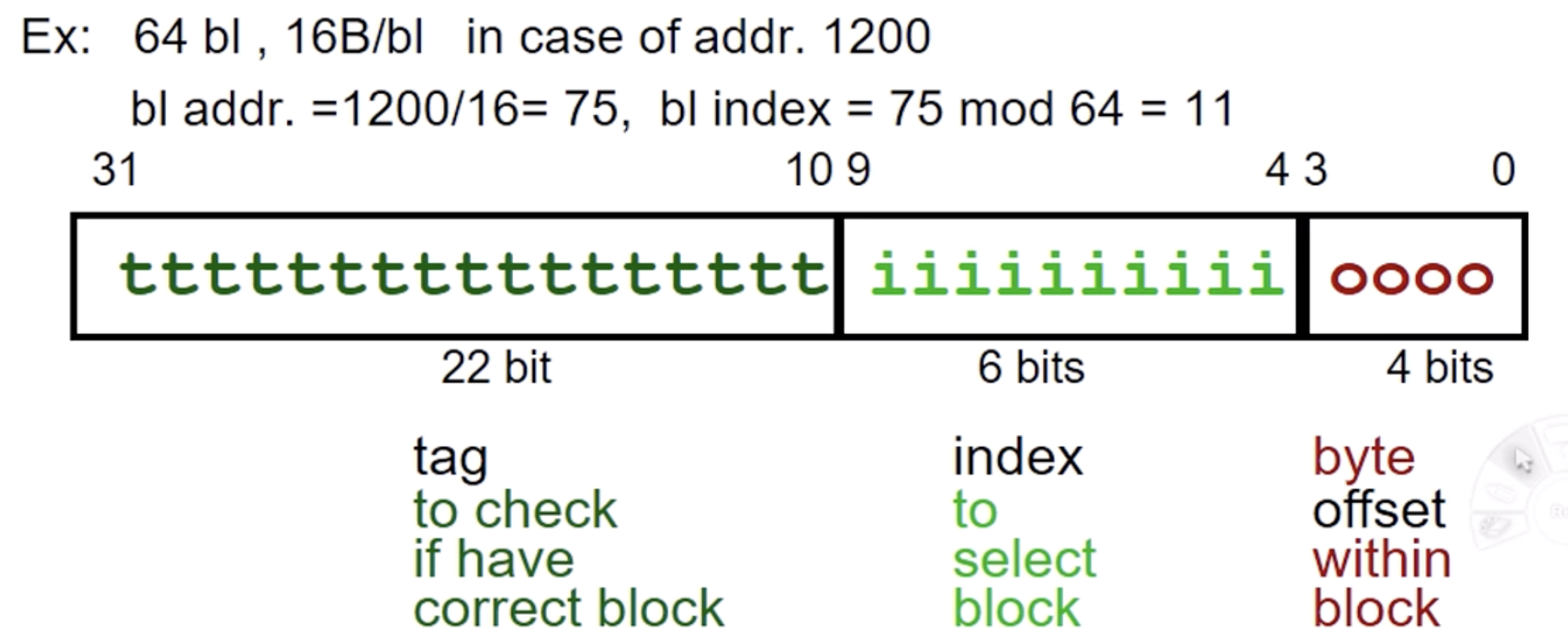
위에서 블록 당 16byte라고 할 때, 1200번째 데이터는 1200 / 16 = 75, 75 % 64 = 11이므로
1200번째 데이터는 75번 블록의 11번 째 인덱스에 위치
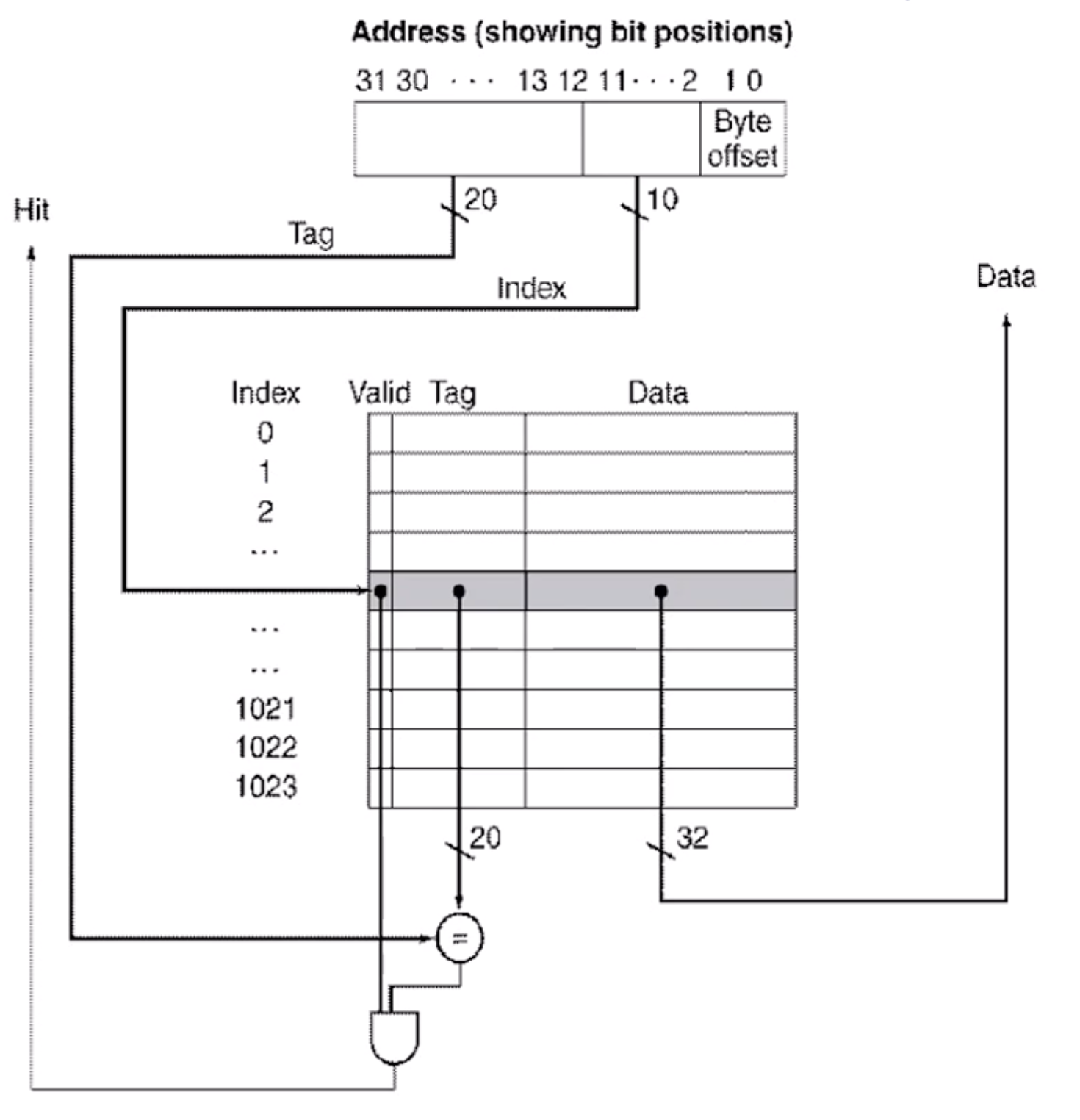
위의 Address에서, Index로 먼저 Cache에서 데이터를 찾고, Valid bit가 1이고 Tag가 같으면 데이터를 사용하고, 그렇지 않은 경우에는 다른 메모리에서 데이터에 접근해야 한다.
이 때 Tag와 Valid bit로 인해 Block Size가 16KB인 시스템의 Cache Block Size는 18.4KB로 공간이 추가적으로 생기는 문제가 생긴다.
Block Size Tradeoff
Block Size를 크게 한 경우, miss rate를 줄일 수 있지만
miss가 난 경우 miss penalty가 굉장히 커지게 된다.
따라서 Block Size를 적절히 정해주는 것이 중요
Average Memory Access Time (AMAT) =Hit Time + Miss Penalty * Miss Rate
Conflict Miss
기본적으로 Cache는 Main memory보다 크기가 작으므로, Miss가 계속 날 수밖에 없지만
이 miss를 줄이는 것이 중요하다.
Set Associative Mapping
Fully Associative Cache
Cache의 전체 Tag를 모두 비교해서 데이터를 가져오는 방식
비교 횟수가 어마어마하게 많아서, 하드웨어가 굉장히 바빠지기 때문에 주로 사용되지는 않는다.
A-way Set Associative
Fully Associative Cache의 단점을 보완한 방식
A-way에서 A는 1, 2, 4, 8, ...이다.
A개의 Tag를 동시에 비교하는 방식
A = 1 --> Direct Mapped
A = Max --> Fully Associative
아래는 4-Way Associative Mapping
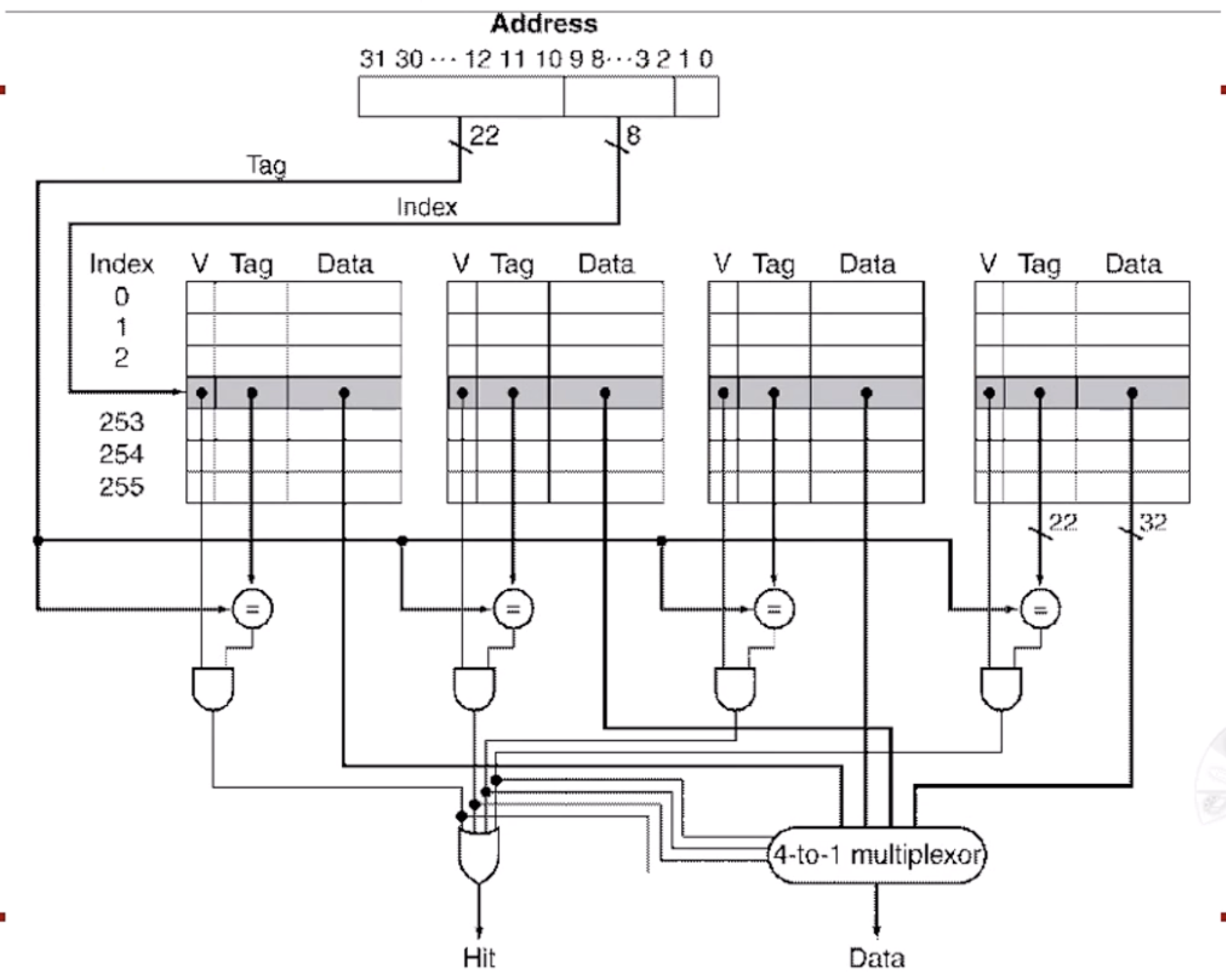
- Overhead가 많이 발생
- 비교가 많으므로 시간이 좀 걸릴 수 있음
- Replacement시 과정이 복잡
Seperate Instruction / Data
Harvard vs. Princeton Architecture
Havard
하버드에서는 이를 분리해서 구성
L1 Cache에서는 분리해서 구성Princeton
프린스턴에서는 이를 같이 구성, 폰 노이만이 이에 기여
L2, L3 Cache에서는 같이 구성
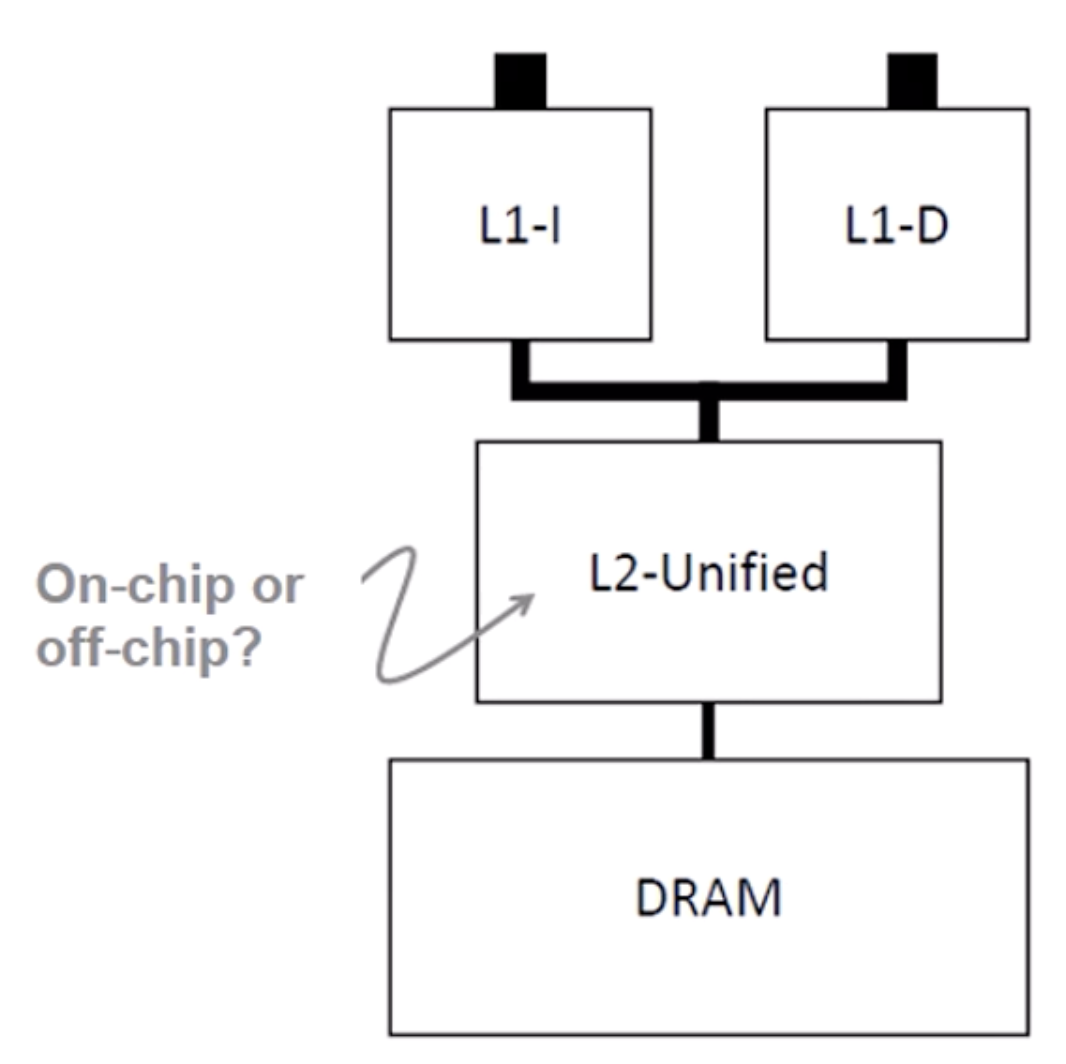
Instruction Cache miss와 Data Cache miss를 잘 다루어 Pipeline에서 문제가 없도록 해야 함
Multy-Level Cache
Miss Penalty를 개선하기 위해 Cache를 여러 단계(L1, L2, LLC(L3))로 나누어 Cache를 구성
1 Cache
AMAT = L1 Hit Time + L1 Miss Rate * L1 Miss Penalty
2 Caches
AMAT = L1 Hit Time + L1 Miss Rate * (L2 Hit Time + L2 Miss Rate * L2 Miss Penalty)
Software Memory Hierarchy
소프트웨어에서 현재 사용될 데이터가 일시적인지를 판단하여 Cache를 구성하는데 도움을 줌
Measure Cache Performance
