[Quantum Computing] Week 10 : 양자 회로의 기초 II

Week 10 : 양자 회로의 기초 II

Multiple qubits

• 양자 컴퓨팅에서 다중 큐비트(Multiple Qubits) 개념을 설명
  • 임의의 단일 큐비트 A,B는 이전 강의에서 배운것과 같이 아래 식으로 정의된다.
    $|\psi\rangle_A = \alpha|0\rangle_A + \beta|1\rangle_A$
    $|\psi\rangle_B = \alpha|0\rangle_B + \beta|1\rangle_B$
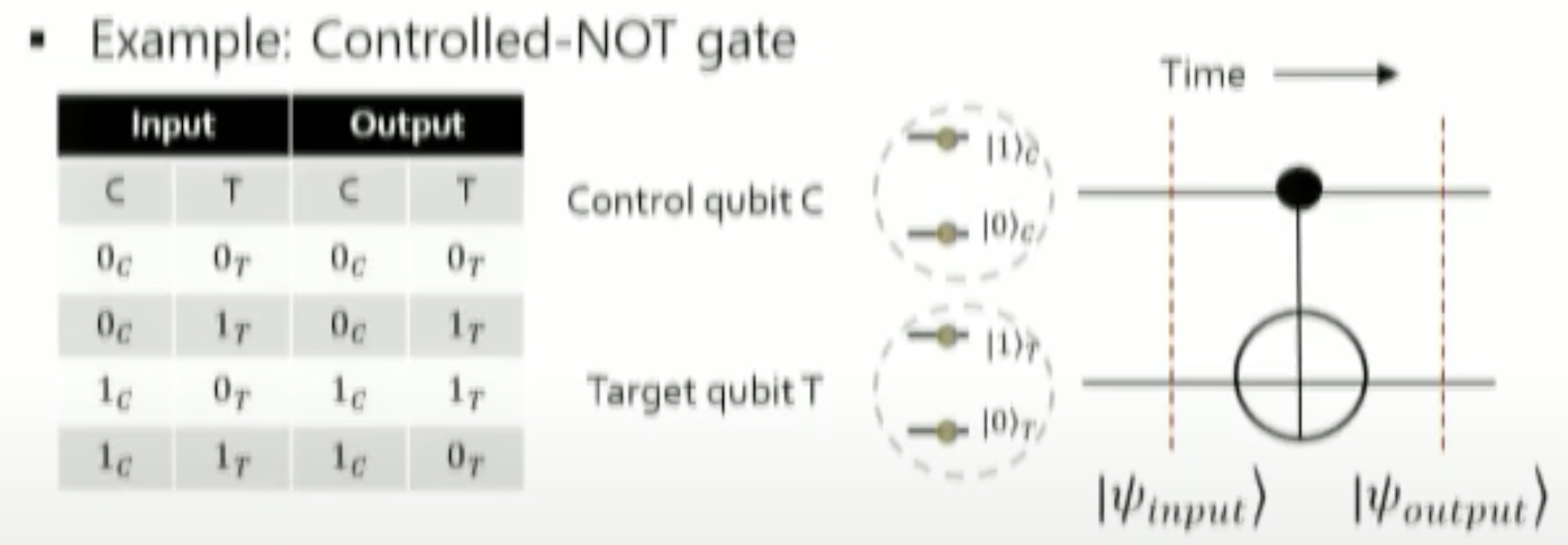
  • 이후 예시로, qubit A의 상태에 따라 qubit B에서 NOT 게이트를 적용할지 말지 조절하는 아래와 같은 Controlled-NOT Gate(CNOT Gate)가 있다고 가정
    
  • 각각의 큐비트가 서로 독립적인 경우만 가정한다면 위 게이트를 양자역학적으로 설명할 수 없음..이때 각각의 큐비트를 나타내는 basis 벡터들은 각각의 독립적인 Hilbert Space 내에 존재함.
  • 그러나 두 큐비트의 상태를 상호작용 하는 결과로 바꿀 수 있음. 즉, 각 큐비트의 basis 벡터를 포함하는 더 큰 Hilbert Space 공간 내 basis 벡터로 나타내어 두개 이상의 큐비트가 상호작용하도록 나타낼 수 있음.
    CNOT gate의 경우 아래와 같이 두 큐비트의 전체 상태를 힐베르트 공간(Hilbert Space)의 단일 벡터로 표현가능하다!
    $|\psi\rangle_{AB} = \alpha|0\rangle_A|0\rangle_B + \beta|0\rangle_A|1\rangle_B + \gamma|1\rangle_A|0\rangle_B + \delta|1\rangle_A|1\rangle_B$

Tensor product

• 따라서 Tensor product를 통해 두 힐베르트 공간 $𝑉$와 $𝑊$의 크기 $𝑚$과 $𝑛$을 곱하여 새 Hilbert Space $𝑉⊗𝑊$를 생성함. 이때, 새로운 Hilbert Space $𝑉⊗𝑊$의 크기는 $𝑚𝑛$ 이다.
  위 CNOT gate의 수식을 아래와 같이 표현가능함. $𝑉⊗𝑊$의 요소는 $V$와 $𝑊$의 요소 간의 텐서곱 선형 조합으로 표현. 즉 $V$와 $W$ 요소의 가능한 모든 조합들로 표현됨!

  $|\psi\rangle_{AB} = \alpha|0\rangle_A \otimes |0\rangle_B + \beta|0\rangle_A \otimes |1\rangle_B + \gamma|1\rangle_A \otimes |0\rangle_B + \delta|1\rangle_A \otimes |1\rangle_B$

• 이때 $𝑉⊗𝑊$의 basis 벡터 : $V$와 $𝑊$의 직교 기저 $∣i⟩$와 $∣j⟩$를 사용하여
  $∣i⟩⊗∣j⟩$로 정의

• Linear operator
  그렇다면, 각각의 Hilbert Space $𝑉$와 $𝑊$에 존재하는 Operator $A,B$가 있을 때 이들이 조합된 공간인 $𝑉⊗𝑊$ 에서의 Operator 선형 조합은 어떻게 나타낼까?

  • $A⊗B$ 로 정의함.
    $(A \otimes B)(|\psi\rangle \otimes |\phi\rangle) = (A|\psi\rangle) \otimes (B|\phi\rangle)$
  • 이 선형조합된 Linear Operator $A⊗B$의 의미는, 조합되기 이전 각각의 공간에 존재하는 각 operator와 벡터간 결과값을 우선 구한 후에 이들의 텐서곱 조합으로 나타냄. 수식으로 표현하면 아래와 같음.
    $(A \otimes B)\left(\sum_i a_i|v_i\rangle \otimes |w_i\rangle\right) = \sum_i a_i (A|v_i\rangle \otimes B|w_i\rangle)$

• Simplified Notation
  Linear Operator $A⊗B$를 단순히 나타내면 아래와 같이 나타낼 수 있다.

  $|v\rangle \otimes |w\rangle \rightarrow ∣v⟩∣w⟩, ∣v,w⟩ \text{or} ∣vw⟩$

  예시)

  $|0\rangle_A \otimes |1\rangle_B \rightarrow |0\rangle_A|1\rangle_B \quad \text{or} \quad |01\rangle$

• Example 1 : CNOT gate
  

  • 입력값이 $|\psi_{\text{input}}\rangle = |0_C\rangle|0_T\rangle$ 일 경우
    $|\psi_{\text{output}}\rangle = |0_C\rangle|0_T\rangle$
  • 입력값이 $|\psi_{\text{input}}\rangle = |1_C\rangle|0_T\rangle$ 인 경우
    $|\psi_{\text{output}}\rangle = |1_C\rangle|1_T\rangle$
  • 입력값이 0,1 사이의 중첩($|\psi_{\text{input}}\rangle = \frac{1}{\sqrt{2}}(|0_C\rangle + |1_C\rangle)|0_T\rangle$) 일 경우, 아래와 같은 선형 조합으로 출력값을 나타낼 수 있다.
    $|\psi_{\text{output}}\rangle = \frac{1}{\sqrt{2}}(|0_C\rangle|0_T\rangle + |1_C\rangle|1_T\rangle)$

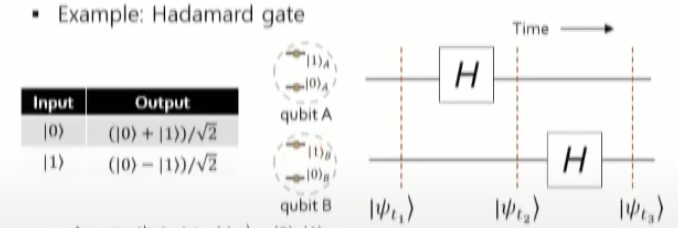
• Example 2 : Hadamard gate
  아래와 같은 Hadamard gate가 있다고 가정함.
  

1. 시간 t1에서는 큐비트 A,B가 모두 초기상태 $|0\rangle_A,|1\rangle_B$ 이다.

2. 시간 t2에서는 큐비트 A에 대해서만 Hadamard gate를 적용하고, 큐비트 B에 대해서는 Hadamard gate를 적용하지 않음.

   $|\psi_{t_2}\rangle = (H_A \otimes I_B)(|0\rangle_A \otimes |1\rangle_B)$
   $|\psi_{t_2}\rangle = H_A|0\rangle_A \otimes I_B|1\rangle_B = \frac{|0\rangle_A + |1\rangle_A}{\sqrt{2}} \otimes |1\rangle_B$
   $|\psi_{t_2}\rangle = \frac{|0\rangle_A|1\rangle_B + |1\rangle_A|1\rangle_B}{\sqrt{2}}$

3. 시간 t3에서는 큐비트 A에 대해서는 Hadamard gate를 적용하지 않고, 큐비트 B에 대해서만 Hadamard gate를 적용함.
   하지만 이미 시간 t2에서 큐비트 A에 대해 Hadamard gate가 적용된 이후 상태이다.

   $|\psi_{t_3}\rangle = (H_A \otimes H_B)(|0\rangle_A \otimes |1\rangle_B)$
   $|\psi_{t_3}\rangle = \frac{|0\rangle_A + |1\rangle_A}{\sqrt{2}} \otimes \frac{|0\rangle_B - |1\rangle_B}{\sqrt{2}}$

   이를 풀어서 계산하면..

   $|\psi_{t_3}\rangle = \frac{|0\rangle_A|0\rangle_B - |0\rangle_A|1\rangle_B + |1\rangle_A|0\rangle_B - |1\rangle_A|1\rangle_B}{2}$

• Tensor product의 Matrix Representation 방법
  텐서곱의 행렬 표현 시, 아래와 같은 두 행렬 A,B에 대해

  $A = m \times n$
  $B = p \times q$

  일때, $A⊗B$의 행렬을 다음과 같이 계산한다.

  $A \otimes B = \begin{bmatrix} A_{11}B & A_{12}B & \cdots & A_{1n}B \\ A_{21}B & A_{22}B & \cdots & A_{2n}B \\ \vdots & \vdots & \ddots & \vdots \\ A_{m1}B & A_{m2}B & \cdots & A_{mn}B \end{bmatrix}$

  이러한 방식을 Kronecker product(크로네커 곱)이라고도 한다.

• 텐서곱은 두 Hilbert 공간에서 독립적인 선형 연산을 결합하여 더 큰 공간에서의 새로운 operator를 생성할 수 있다! 아래는 강의자료에 포함된 예시이다.

  $C = \sum_j c_j A_j \otimes B_j$
  $C(|v\rangle \otimes |w\rangle) = \sum_j c_j (A_j|v\rangle \otimes B_j|w\rangle)$

• 텐서곱 공간에서의 내적(inner product)

  • 텐서곱 공간에서 두 상태의 내적은 아래와 같이 정의됨.
    $\left(\sum_i a_i\langle v_i|\right)\left(\sum_j b_j|w_j\rangle\right) \cdot \left(\sum_k a_k'\langle v_k'|\right)\left(\sum_l b_l'|w_l'\rangle\right) = \sum_{i,j} a_i b_j \langle v_i|v_k'\rangle \langle w_j|w_l'\rangle$
  • 텐서곱은 아래와 같은 기호로도 나타낼 수 있다.
    $(|\psi\rangle)^{\otimes 2} = |\psi\rangle \otimes |\psi\rangle, \quad (|\psi\rangle)^{\otimes k} = |\psi\rangle \otimes |\psi\rangle \otimes \cdots \otimes |\psi\rangle \, (k \text{ times})$
    $H^{\otimes 2} = H \otimes H, \quad H^{\otimes k} = H \otimes H \otimes \cdots \otimes H \, (k \text{ times})$

References

• [서울대학교 공과대학]양자 컴퓨팅 및 정보의 기초 10. 양자 회로의 기초 II