[Quantum Computing] Week 11 : 양자회로의 기초-III

Week 11 : 양자회로의 기초-III

Quantum circuits

• 양자 컴퓨팅에서 양자 알고리즘을 시뮬레이션하거나 실행하는 데 사용되는 일종의 모델
• 일반적으로, 양자 회로는 보통 qubit을 연결하는 wire와 gate symbol로 표현됨.
  • 이때, wire는 반드시 물리적인 wire를 의미하는것은 아니며 시간의 흐름 혹은 광자의 이동 경로가 될 수 있음.
• 양자회로의 예시는 아래 SWAP 회로를 예시로 설명하였다.
  
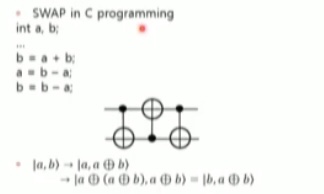
  • 위 회로에서 확인할 수 있듯이, 양자 게이트를 사용하여 두 큐비트의 상태를 교환가능함.
  • 입력상태 $∣a,b⟩$에서 시작하여, 중간 계산 과정에서 XOR 연산(⊕)을 수행. 최종적으로 $∣b,a⟩$ 상태로 변환됨을 확인

Comparison with classical circuits

• Feedback(혹은 loop)는 양자회로에서는 허용되지 않음.
  • 양자회로는 비순환 그래프(acyclic)로 구성되어야 함!
• 양자회로에서, FANOUT/FANIN 이 존재할 수 없음.
  • 그 이유는? 양자회로에서의 변환은 Unitary Transform을 만족해야 하는 성질이 존재하기 때문
  • 따라서 Non-Cloning Theorem에 의해 양자상태를 복제하는것은 불가능하며
  • 양자회로는 가역적이므로 다중입력의 결합이 불가능.
  • 즉, 양자회로 내에서 입력 qubit 갯수와 출력 qubit 갯수가 다른 회로는 존재할 수 없다.

Controlled-U gate

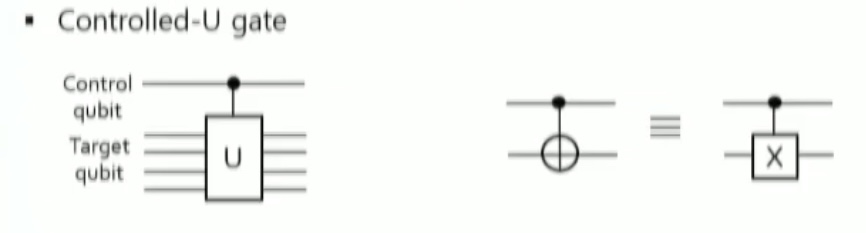
• 제어 큐비트(Control Qubit)와 대상 큐비트(Target Qubit)로 구성되며, 제어 큐비트의 상태에 따라 대상 큐비트에 연산 $U$가 적용되는 게이트이다.
• 제어 큐비트가 $∣1⟩$ 일때 대상 큐비트에 X gate(NOT gate)가 적용됨.
• 양자회로에서는 일반적으로 제어점과 XOR 게이트로 아래와 같이 표현된다.
  

Measurement symbol

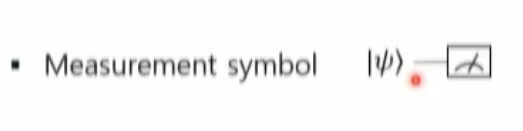
• 이는 $∣ψ⟩$ 상태의 큐비트를 측정하는 과정을 설명한다.
• Measurement symbol은 위 그림과 같이 박스와 화살표로 표현되며, 측정결과 $∣ψ⟩$ 상태의 큐비트는 $∣0⟩$ 또는 $∣1⟩$로 붕괴된다.

Qubit 복사가 불가능한 이유

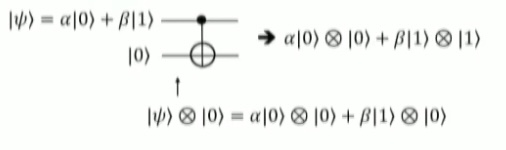
• 본 강의에서는 위와같은 CNOT 게이트를 사용한 Qubit 복사의 가능성을 검증한다.
• 이때 복사란, 초기 qubit 상태인 $∣ψ⟩$를 초기상태 그대로 복사하려는 것이며
  CNOT 게이트 적용결과 아래와 같은 복사결과를 얻는 것임.
  $|\psi\rangle \otimes |\psi\rangle = (\alpha|0\rangle + \beta|1\rangle) \otimes (\alpha|0\rangle + \beta|1\rangle)$
• 그러나 실제로는 위와같은 CNOT 게이트 연산결과는 아래 결과와 같이 얽힘현상이 발생하게 된다.
  $|\psi\rangle \otimes |0\rangle = (\alpha|0\rangle + \beta|1\rangle) \otimes |0\rangle$
  $\alpha|0\rangle|0\rangle + \beta|1\rangle|1\rangle$
• 즉 결론적으로 알려지지 않은 임의의 양자 상태를 완벽하게 복사하는 것은 불가능하며, 복제 과정에서 큐비트의 중첩 상태가 깨지거나 얽힘이 발생하기 때문에 최초에 원하는 복사 결과와 다르게 나타나게 됨을 알 수 있다.
  -> No Cloning Theorem(증명과정은 생략)

Measurement in other basis

• 일반적인 기저벡터인 $∣0⟩,∣1⟩$ 외에 다른 기저에서 qubit를 측정하는 방법은? 아래와 같이 $∣+⟩, ∣-⟩$의 basis 에서의 측정도 생각해볼 수 있다.
  $|\psi\rangle = \alpha|0\rangle + \beta|1\rangle$
  에서, $∣+⟩, ∣-⟩$ basis 벡터로 재표현하면 아래와 같이 나타난다.
  $|\psi\rangle = \alpha\frac{|+\rangle + |-\rangle}{\sqrt{2}} + \beta\frac{|+\rangle - |-\rangle}{\sqrt{2}}$
  $|\psi\rangle = \frac{\alpha + \beta}{\sqrt{2}}|+\rangle + \frac{\alpha - \beta}{\sqrt{2}}|-\rangle$
• 위와 같은 방식처럼, 다른 기저에서의 측정은 아래와 같이 수행할 수 있다.
  • Polarization : Spliter를 회전시켜 다른 기저벡터를 얻음.
  • Two-level atom : Hadamard gate를 활용하여 $∣0⟩,∣1⟩$ 벡터를 $∣+⟩, ∣-⟩$로 변환할 수 있다.
• 그렇다면 다른 기저에서의 measurement가 필요한 이유는?
  • 특정 시점에서의 양자 상태의 상대적인 위상을 확인하기 위해
  • Quantum Teleportation을 위해서는 다른 기저에서의 측정이 필수적이기 때문!

Bell basis

• 아래와 같은 두 qubits A,B가 있다고 가정할때 아래와 같은 벡터 조합을 만들 수 있다.

• 이들이 각각 orthogonal 한가?

  • 위의 모든 벡터는 서로 직교

• 이들이 complete basis 인가?

  • complete basis란 임의의 어떤 공간이 주어지고 주어진 공간에 특정 basis가 있을 때, 해당 공간 내 존재하는 임의의 모든 벡터를 특정 basis로 나타낼 수 있을때 이 특정 basis를 complete basis라고 함.
  • 4차원 공간 내에서 4개의 벡터가 서로 직교하므로, complete basis를 만족

• 즉, 결론적으로 Bell basis는 임의의 두 qubits A,B로 이루어진 임의의 벡터는 항상 위 4가지 벡터의 선형 조합으로 나타낼 수 있음을 설명하는 이론!

• 따라서 위 4가지 벡터들을 Bell basis(또는 Bell state, EPR state, EPR pair)라고 부름.

• 그렇다면 이러한 Bell state를 어떻게 생성할까

  • 아래와 같은 Entangling circuit로 생성 가능하다
    
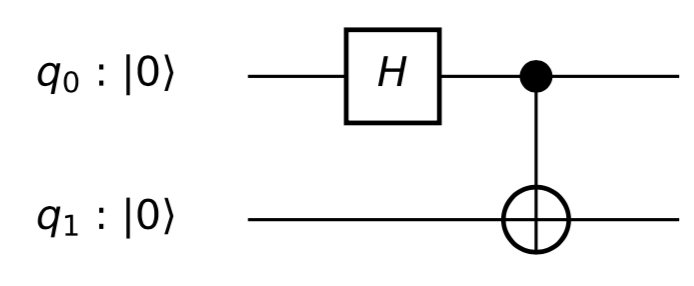
    1. 첫 번째 큐비트(q0)에 Hadamard 게이트(H)를 적용하여 중첩을 만듬
    2. 두 번째 큐비트(q1)와 첫 번째 큐비트(q0) 사이에 CNOT 게이트를 적용하여 얽힘 상태를 만듬

  • Entangling circuit의 input/output 결과는 아래 표와 같이 나타난다.

    $\begin{array}{|c|c|c|} \hline \text{Input} & \text{Output (Bell State)} \\ |A\rangle = |0\rangle, |B\rangle = |0\rangle & |\phi^+\rangle = \frac{|00\rangle + |11\rangle}{\sqrt{2}} \\ |A\rangle = |0\rangle, |B\rangle = |1\rangle & |\psi^+\rangle = \frac{|01\rangle + |10\rangle}{\sqrt{2}} \\ |A\rangle = |1\rangle, |B\rangle = |0\rangle & |\phi^-\rangle = \frac{|00\rangle - |11\rangle}{\sqrt{2}} \\ |A\rangle = |1\rangle, |B\rangle = |1\rangle & |\psi^-\rangle = \frac{|01\rangle - |10\rangle}{\sqrt{2}} \\ \hline \end{array}$

• Bell basis의 측정

  • Bell basis의 측정은 어떻게 수행할 수 있는가 -> 아래 회로와 같이 Bell basis(EPR pair)를 Entangling circuit의 반대로 통과시켜서 측정할 수 있음!
    
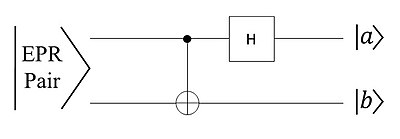
  • 이는 bell basis를 복원하거나, 측정 전 분리된 기저 상태로 변환하는데 활용됨
    $\begin{array}{|c|c|} \hline \text{Input (Bell State)} & \text{Output (Separable State)} \\ |\phi^+\rangle = \frac{|00\rangle + |11\rangle}{\sqrt{2}} & |A\rangle = |0\rangle, |B\rangle = |0\rangle \\ |\psi^+\rangle = \frac{|01\rangle + |10\rangle}{\sqrt{2}} & |A\rangle = |0\rangle, |B\rangle = |1\rangle \\ |\phi^-\rangle = \frac{|00\rangle - |11\rangle}{\sqrt{2}} & |A\rangle = |1\rangle, |B\rangle = |0\rangle \\ |\psi^-\rangle = \frac{|01\rangle - |10\rangle}{\sqrt{2}} & |A\rangle = |1\rangle, |B\rangle = |1\rangle \\ \hline \end{array}$

References

• [서울대학교 공과대학]양자 컴퓨팅 및 정보의 기초 11. 양자 회로의 기초 III