Week 9: 양자 회로의 기초 I
Uncertainty Principle(불확정성의 원리)
-
빛의 상태를 측정하는 아래와 같은 편광 측정 상태를 가정해보자.
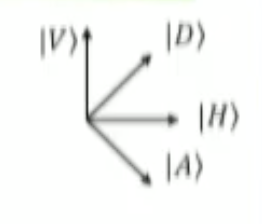
- 초기상태 : 이며
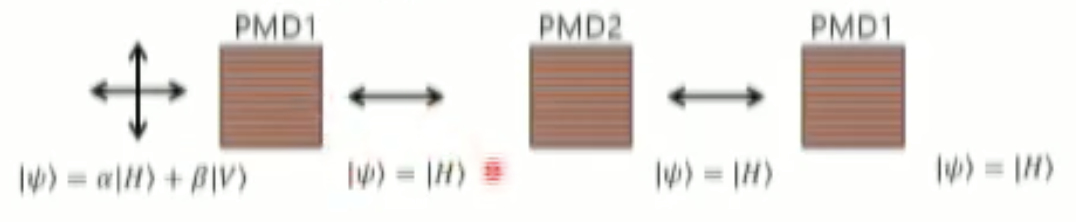
- 이때 : 수평 편광 상태, : 수직 편광 상태를 나타내며 이를 통한 편광 측정기 PMD1, PMD2는 아래와 같다.
- PMD1 : 측정시 +1, 측정시 -1을 출력한다.
- PMD2 :
- 이 경우 PMD1에서 최초 측정한 결과가 PMD1 -> PMD2 -> PMD1 로 측정하였을때 측정값이 바뀌지 않음.
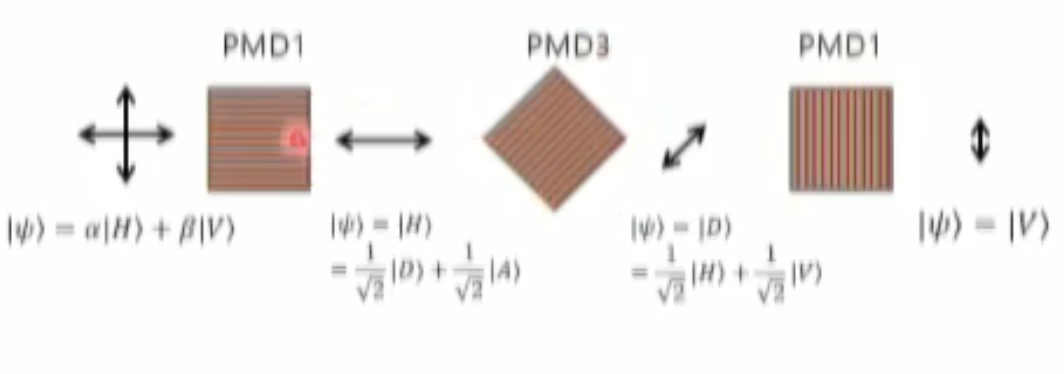
- 를 basis로 하여 편광 측정을 하는 PMD3는 아래와 같다.
- PMD3 :
- 이 경우 PMD1에서 최초 측정한 결과가 PMD1 -> PMD2 -> PMD1 로 측정하였을때 측정값이 바뀌게 됨!
-
즉 편광 측정을 통해, 양자 상태의 측정 결과가 PMD와 같은 특정한 측정기에 의존하며 하나의 측정 결과로 모든 정보를 얻는 것이 불가능하다는 불확정성 원리를 시각적 및 실험으로 설명할 수 있음.
-
불확정성 원리와 commute 관계
- commute 정의 :
- 두 operator의 commute 결과값, 즉 일 경우 동시에 정확하게 측정 가능하며 PMD1, PMD2와 같이 측정값이 변하지 않음.
- 일 경우, 동시에 정확한 측정이 불가능하며 PMD1,PMD3와 같이 측정값이 변하게 됨.
Collapse of Quantum State(양자상태의 붕괴)
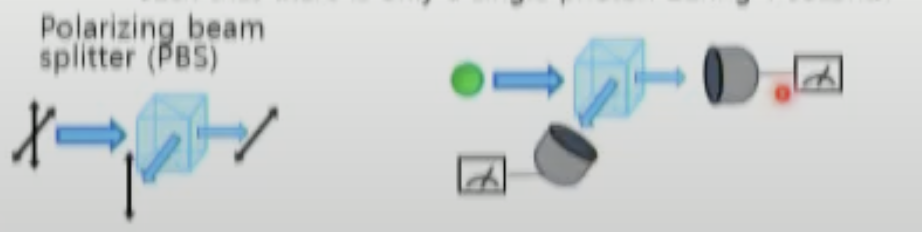
- 편광 상태를 점차 약하게 만들어 단일 광자(Photon) 상태로 만들면 어떻게 될까?
- (양자역학적 해석) 광자의 갯수에 상관없이, 측정될 때마다 양자 상태가 붕괴하여 새로운 상태로 바뀌는 현상이 관찰됨. 예를들면, 편광상태 에서 측정 시 , 중 하나의 상태로 특정 확률에 따라 붕괴가 된다.
- (고전 물리학) 고전 물리학은 광자를 연속적인 전자기파로 간주하며, 단일 광자의 개념을 다루지 않음. 단일 광자 수준에서는 이러한 해석이 불가능하다...
- 이러한 편광측정 실험을 통해 빛은 입자로 이루어짐을 확실히 알 수 있음. 단일 광자 수준에서는 양자역학이 유일하게 관찰 결과를 설명할 수 있는 이론이 된다.
Quantum Bits(Qubit)
- Qubit : 이진수 0과 1의 선형 조합으로 표현되는 2차원 복소 벡터 공간에서의 벡터
- 임의의 큐비트
- 이러한 큐비트를 측정 시 는 0 또는 1으로 붕괴하며 그 확률은 아래와 같음.
- 0일 확률 :
- 1일 확률 :
- 그러나 한번의 측정만으로는 측정 후 양자의 상태가 계속해서 붕괴하며 변화하기 때문에 의 정확한 값을 알 수 없음. 따라서 다양한 basis 벡터에서 여러번 측정을 수행해야 하며 다수의 측정 결과를 통해 의 값을 통계적으로 추정가능함.
Bloch sphere
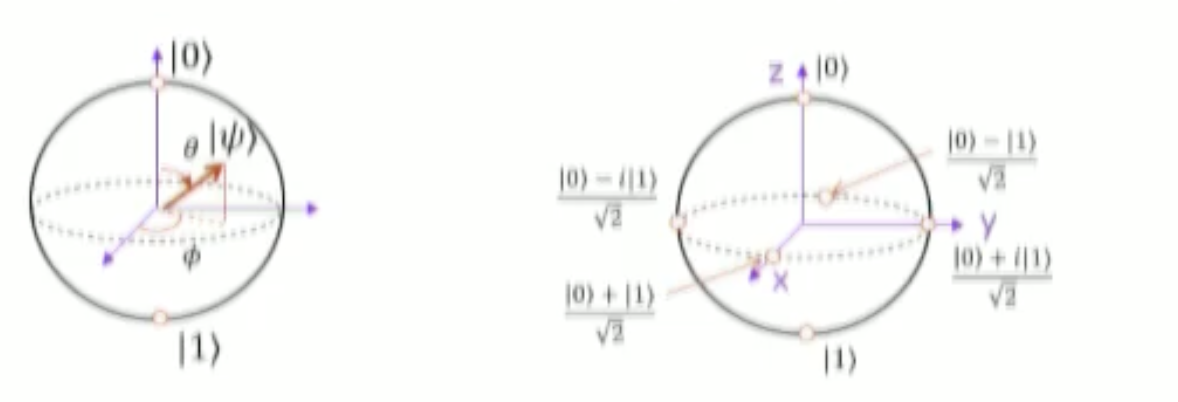
- 큐비트의 상태를 구면 좌표계로 나타내는 시각화 방식
- 임의의 큐비트 에서 를 구면좌표계로 나타내기 위해 아래와 같이 변환할 수 있다.
- 는 global phase(글로벌 위상)으로, 물리적으로 측정 불가능함. 따라서 이 값을 무시하고
로 상태표현 가능
- 위와 같은 방식으로 임의의 큐비트 상태를 구면 좌표계에서 mapping 할 수 있다.
Single-qubit gates
-
큐비트 상태 은 아래와 같이 나타내어진다.
-
X gate : 고전적인 NOT 게이트와 유사하며, 입력 큐비트를 반전시키는 operator
일반적인 큐비트 에서 X gate 동작 시,
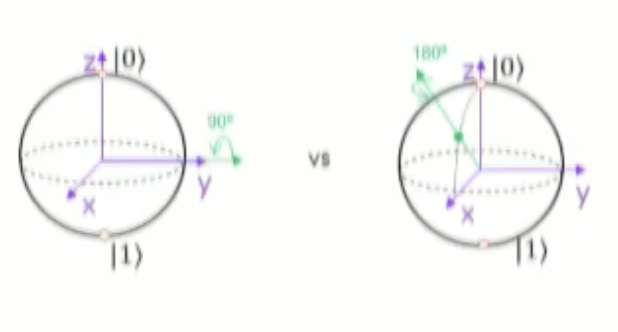
가 된다.- Bloch sphere 에서의 X 게이트 : 큐비트 상태를 X축을 기준으로 180° 회전
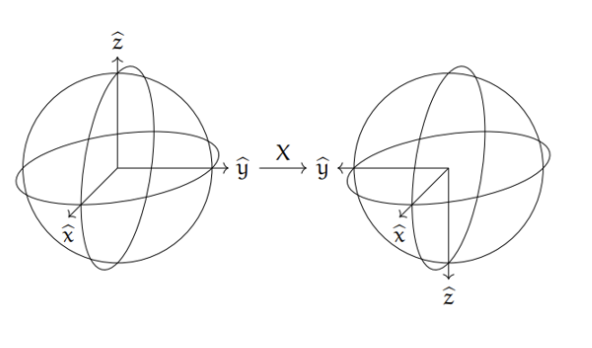
- Bloch sphere 에서의 X 게이트 : 큐비트 상태를 X축을 기준으로 180° 회전
-
Z 게이트 : 상태를 그대로 유지하고, 상태에 음수를 곱함.
- Bloch sphere에서의 Z 게이트 : Z축을 기준으로 180° 회전
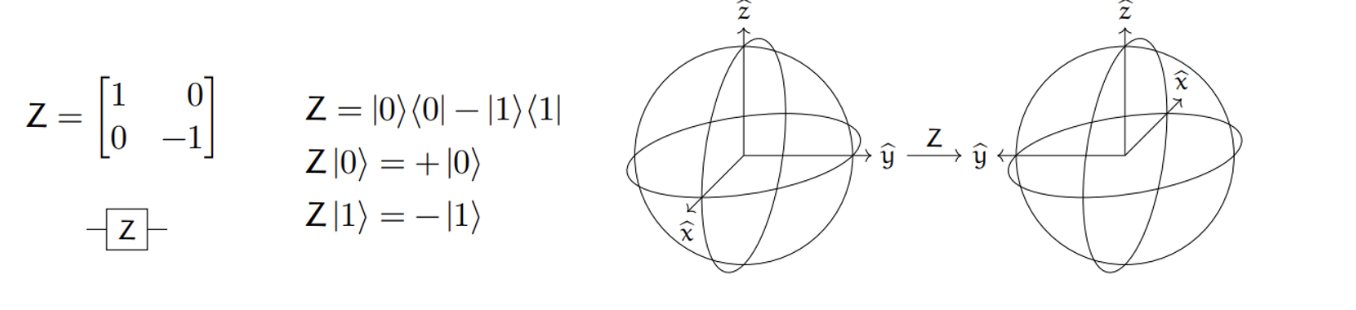
- Bloch sphere에서의 Z 게이트 : Z축을 기준으로 180° 회전
-
Y 게이트는 아래와 같은 행렬로 정의됨
- Y 게이트는 큐비트를 복소수 계수를 포함한 상태로 변환하며, Bloch sphere에서 Y축을 기준으로 180° 회전
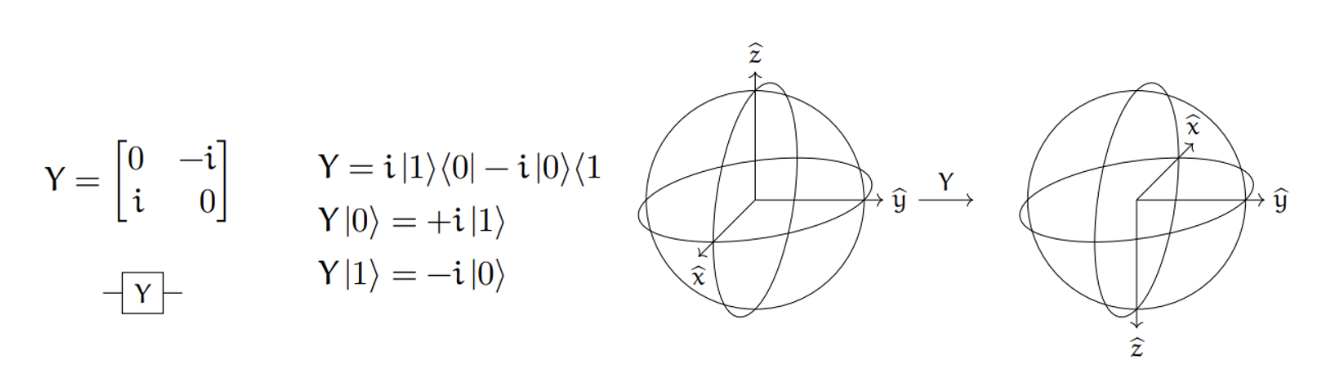
- Y 게이트는 큐비트를 복소수 계수를 포함한 상태로 변환하며, Bloch sphere에서 Y축을 기준으로 180° 회전
-
Hadamard 게이트는 아래 행렬과 같이 정의됨
- 수식을 통해 확인가능한 점은, Hadamard 게이트는 큐비트를 와 상태의 균등한 중첩 상태로 변환하거나, 중첩 상태를 다시 고유 상태로 변환하는 역할을 수행한다는 점이다.
- Hadamard 게이트의 특성 : Hadamard Gate를 두 번 적용하면 원래 상태로 되돌아오게 된다. Single-qubit gate는 Bloch sphere 상에서 회전에 해당되는데, hadamard 게이트는 X,Y,Z축이 아닌 특정한 대각선 축을 기준으로 한 회전이 되며 두번 적용 시 다시 원래 자리로 돌아오게 되는 특성이 있음.
- Bloch Sphere에서의 Hadamard 게이트 : Z축과 X축 사이에서 45° 대각선 축을 기준으로 180° 회전