Week 13 : 양자 알고리즘 I

1. Deutsch's Algorithm (도이치 알고리즘)

1.1 양자 중첩과 병렬성

고전 컴퓨터는 0 또는 1 중 하나의 상태만 가질 수 있지만, 양자 컴퓨터는 0과 1을 동시에 가질 수 있는 중첩(superposition) 상태가 가능하다. 이를 활용하면 여러 가지 경우를 한 번에 계산할 수 있다.

1.2 도이치 알고리즘의 목표

어떤 함수 $𝑓(𝑥)$ 가 항상 같은 값(상수 함수) 을 출력하는지, 아니면 입력에 따라 달라지는 값(균형 함수) 을 출력하는지를 구별하는 문제를 해결하는 알고리즘이다.

고전 컴퓨터 vs. 양자 컴퓨터

• 고전 컴퓨터: 함수를 두 번 실행해야 함 (예: $f(0)$과 $f(1)$을 각각 계산)
• 양자 컴퓨터: 한 번의 계산만으로 두 가지 결과를 동시에 얻을 수 있음

양자 컴퓨터는 중첩(superposition)과 간섭(interference) 을 이용하여 한 번의 계산으로 두 가지 값을 비교할 수 있는 효율적인 방법을 제공한다.

1.3 Hadamard 게이트의 역할

Hadamard 게이트(H 게이트)를 사용하면 0과 1이 동시에 존재하는 상태를 만들 수 있다. 이를 수식으로 표현하면 아래와 같으며, 이 상태를 활용하면 함수를 한 번만 평가해도 두 가지 값을 비교할 수 있게 된다.

구체적 예시는 아래의 함수 구분 문제 예가 있다.
디지털 회로에서는 이를 구분하기 위하여 $F(0), F(1)$을 각각 계산하여 두번의 연산이 필요하지만, 양자회로에서 Hadamard 게이트를 활용할 경우 한번의 연산으로 $F(0), F(1)$ 중첩 상태를 생성할 수 있다.

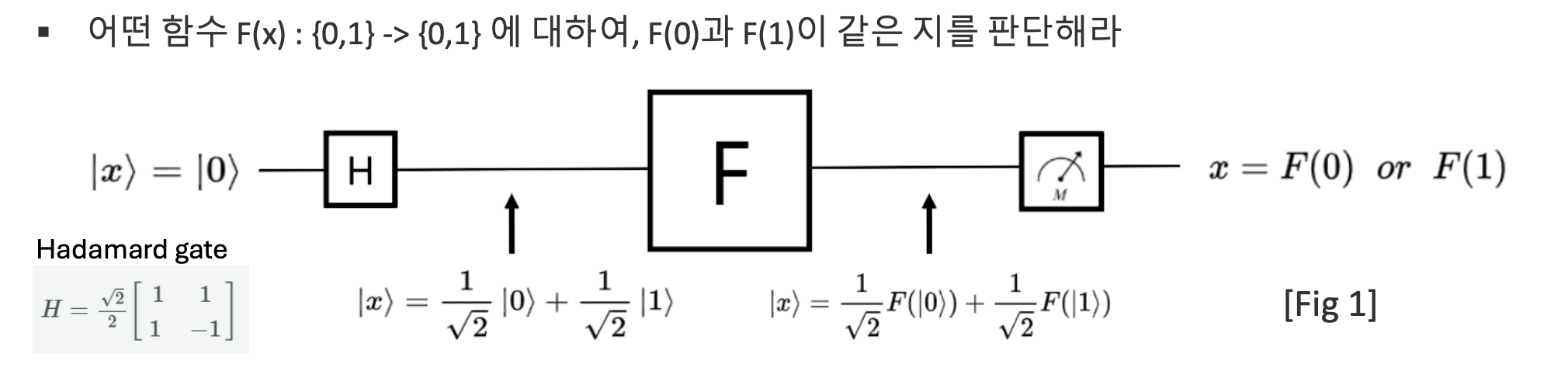
그러나 이 경우 하나의 문제점이 존재하는데, 중첩상태에서 $F(0), F(1)$를 동시 계산 가능하지만 양자역학의 특성상 관측할 경우 하나의 값만 남고 다른 값이 사라지게 된다.
따라서 관측 없이 정보를 얻을 방법이 필요해졌고, 그 해결책으로 제안된 방법이 양자 간섭(Interference)을 활용하는 방안이 제안되었다.

2. Reversible Gates (가역 게이트)와 Fredkin Gate

2.1 Fredkin Gate (프레드킨 게이트)

Fredkin Gate는 CSWAP (Controlled-SWAP) 게이트 라고도 불린다.

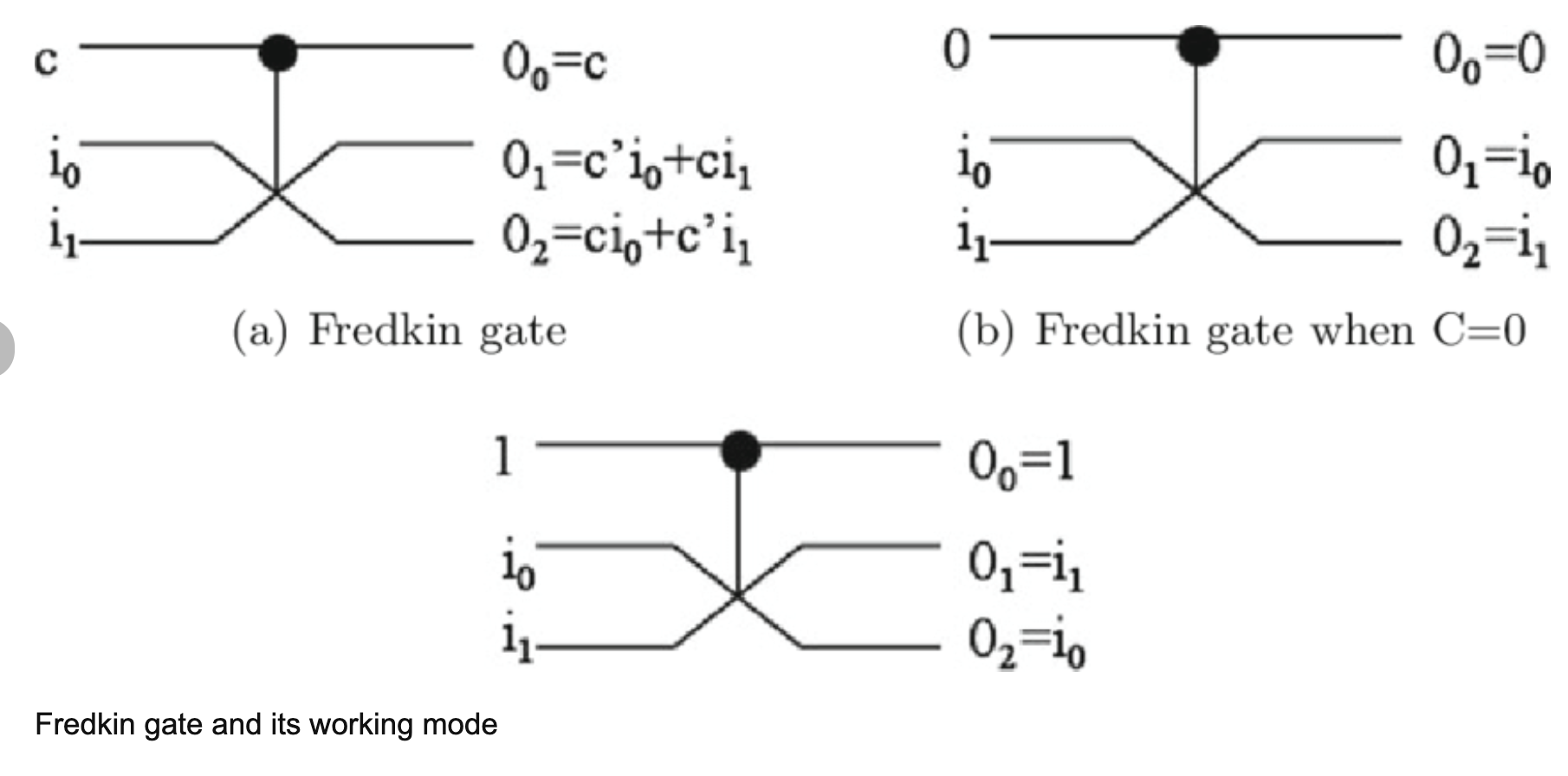
동작 원리

• 입력 큐비트가 3개 → 출력 큐비트도 3개
• 첫 번째 큐비트(컨트롤 큐비트)가 1이면 → 두 번째, 세 번째 큐비트 위치를 바꿈 (스왑)
• 컨트롤 큐비트가 0이면 → 그대로 유지

특징

• Reversible(되돌릴 수 있음) → 연산을 거꾸로 하면 원래 상태로 복구 가능
• AND 게이트, NOT 게이트 구현 가능 → 디지털 회로 설계에 도움 됨
• 그러나, 가비지 큐비트(불필요한 큐비트) 가 생길 수 있으며, 이는 양자 연산의 정확성을 저하시킬 수 있다.

그러나, 이러한 Fredkin gate의 특성상 가비지 큐비트(불필요한 큐비트) 가 생길 수 있으며, 이는 양자 연산의 정확성을 저하시킬 수 있다는 한계점이 존재함.

3. 양자 상태 측정의 문제점

양자 회로에서 측정이 문제가 되는 이유는?

• 큐비트를 측정하면 상태가 변할 수 있음
  • 잡음이나 외부 요인으로 인해 원래 의도한 값과 달라질 수도 있음
• 한 큐비트가 0으로 결정된다면? 이 경우, 다른 큐비트들도 0과 1로 고정될 위험이 존재함
• 즉, 양자회로에서 측정 시 중첩(superposition) 상태가 붕괴되며, 불필요한 측정이 연산 결과를 엉망으로 만들 수 있다.

따라서, 양자 알고리즘에서는 중첩 상태를 유지하는 것이 핵심이다.

4. Uncomputation (언컴퓨테이션)

Uncomputation이란 필요한 데이터만 남기고 불필요한 큐비트를 제거 하는 과정을 말한다.

동작 원리

• 큐비트가 얽혀 있는 상태에서 Unitary gate로 역 연산 수행
• 초기 상태로 복원하여 불필요한 큐비트 해제

Uncomputation을 통해 가비지 큐비트를 줄여 양자 회로의 리소스를 절약 할 수 있고 양자 알고리즘의 효율성을 높여 연산 오류를 방지가능하다. 또한 앞서 언급한 Fredkin Gate에서 가비지 큐비트가 발생한다는 문제점을 해결할 수 있다.

즉, Uncomputation은 불필요한 큐비트를 제거해 양자 연산을 최적화하는 핵심기술이다!

5. Shor’s Algorithm (쇼어 알고리즘)

쇼어 알고리즘은 양자 푸리에 변환(QFT) 을 활용하여 정수 $𝑁$ 을 소인수분해하는 알고리즘이다.

기존 고전적 방법의 소인수 분해 알고리즘은 큰 수의 소인수분해가 어려운 성질 에 의존한다. 고전적인 소인수분해 방법의 대표적인 특성은 아래와 같음

• 완전탐색(Trial Division): 모든 소수로 나누어 보며 소인수를 찾음 → $O(2^n)$의 시간 복잡도를 가짐

반면, 쇼어 알고리즘에서는 정수 $𝑁$ 의 소인수를 찾기 위해 주기성(periodicity)을 활용하여 소인수를 분해하는 접근법을 제안한다. 따라서 기존 고전적 방법 대비 $O(n^3)$의 시간복잡도를 나타낸다.

따라서 이는 현재의 고전 컴퓨터로는 해결할 수 없는 소인수분해 문제를 양자 컴퓨터가 쇼어 알고리즘을 통해 현실적으로 해결 가능하다는 의미가 될 수 있다.

최근 RSA 암호 해독의 핵심 기술인 빠른 소인수분해를 쇼어 알고리즘을 활용해 가능하게 하여 기존 암호 체계를 위협하는 연구들이 지속적으로 수행되고 있다.

References

• [서울대학교 공과대학]양자 컴퓨팅 및 정보의 기초 13. 양자 알고리즘 I
• https://www.researchgate.net/figure/Fredkin-gate-and-its-working-mode_fig1_291274046