[Quantum Computing] Week 7 : 양자역학의 공리-1

Week 7 : 양자역학의 공리-1

Example of Quantum states

• Two-level atom
  

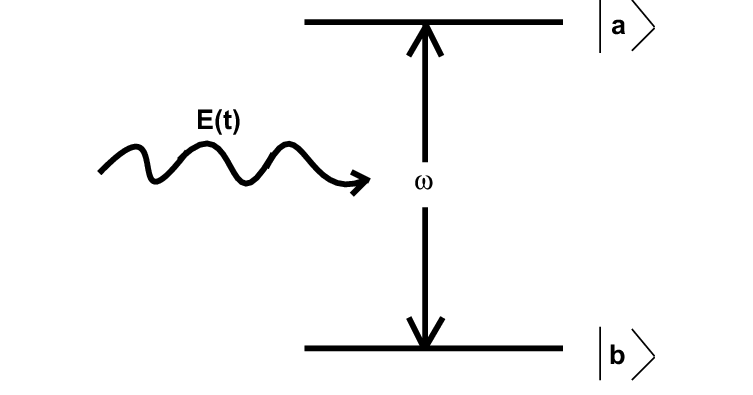
  • 원자는 낮은 에너지 상태(0 상태,$∣g⟩$)와 높은 에너지 상태(1 상태,$∣e⟩$) 두가지 상태만 가진다고 가정
  • 일반적으로 원자가 빛과 상호작용하면, 특정 에너지를 가진 광자를 흡수하여 $∣g⟩$에서 $∣e⟩$로 전이하거나, 반대로 $∣e⟩$에서 $∣g⟩$로 떨어지면서 광자를 방출할 수 있다.
  • 양자역학에서, 어떤 전자의 양자 상태가 Hilbert space 내 임의의 벡터 $∣ψ⟩$로 나타내어지고 이 Hilbert space는 $∣0⟩,∣1⟩$로 나타내어지므로
    $∣ψ⟩ = \alpha∣0⟩+\beta∣1⟩$로 나타낼 수 있다.
  • 즉 양자역학에서 전자는 가질 수 있는 여러가지 에너지 레벨들간에 중첩으로 나타내어지는게 일반적인 양자 상태라고 할 수 있다.

• Polarization of light
  

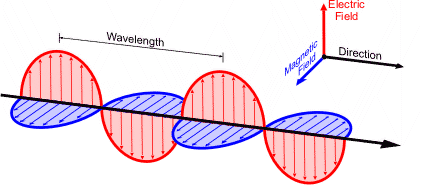
  • 빛은 전자기파로, 전기장과 자기장이 서로 수직으로 진동하며 진행한다. 이 중 전기장의 진동 방향이 편광을 결정한다. 이때 편광은 두개의 수직 축 벡터(수직(Vertical,∣V⟩) 및 수평(Horizontal,∣H⟩))의 조합으로 분해하여 구성할 수 있다. 이를 수식으로 정리하면 아래와 같다.
    • Diagonal : 수평과 수직 편광의 동일한 진폭과 위상이 합쳐진 상태
      • $|D\rangle = \frac{1}{\sqrt{2}} (|H\rangle + |V\rangle)$
    • Antidiagonal : 수평과 수직 편광의 동일한 진폭과 반대 위상이 합쳐진 상태
      • $|A\rangle = \frac{1}{\sqrt{2}} (|H\rangle - |V\rangle)$
    • Right circular : 수평 ($∣H⟩$)과 수직 ($∣V⟩$) 편광 상태가 동일한 진폭을 가지며, $∣V⟩$가 $∣H⟩$보다 90도 위상 차를 가지는 상태
      • $|R\rangle = \frac{1}{\sqrt{2}} (|H\rangle - i|V\rangle)$
    • Left circular : 수평 ($∣H⟩$)과 수직 ($∣V⟩$) 편광 상태가 동일한 진폭을 가지며, $∣V⟩$가 $∣H⟩$보다 -90도 위상 차를 가지는 상태
      • $|L\rangle = \frac{1}{\sqrt{2}} (|H\rangle + i|V\rangle)$
    • $|R\rangle$과 $|L\rangle$은 서로 직교함
    • $|D\rangle$과 $|A\rangle$는 서로 직교함

• Photon(광자)

  • 정의 : 전자기 에너지의 불연속적인 묶음을 운반하는 빛의 입자로 설명된다. 즉 이는 에너지가 양자화(Quantized)되어 있다는 것을 의미함.
  • 단일 photon의 에너지량 : $E = h f = \hbar \omega$
    • $h$: 플랑크 상수 ($h = 6.626 \times 10^{-34}$, $\text{J·s}$)).
    • $\hbar$: 축약 플랑크 상수 $( \hbar = \frac{h}{2\pi}$).
    • $f$: 빛의 주파수.
    • $\omega = 2\pi f$ : 각진동수
  • 양자화된 에너지의 증거?
    • 흑체 복사(Blackbody Radiation): 고전 물리학으로 설명되지 않던 흑체복사 현상을 해결하기 위해 플랑크가 에너지 양자화를 제안함.
      • 흑체복사 현상이란?
      • $E = nhf \quad (n = 0, 1, 2, \dots)$
    • 광전 효과(Photoelectric Effect): 특정 주파수 이상의 빛만이 전자를 방출할 수 있다는 현상
    • 콤프턴 효과(Compton Effect): 광자가 입자처럼 운동량을 가지며 산란 현상을 설명할 수 있다.

References

• [서울대학교 공과대학]양자 컴퓨팅 및 정보의 기초 7. 양자역학의 공리 I
• https://www.researchgate.net/figure/nteraction-of-a-single-two-level-atom-with-an-optical-field_fig1_283475893
• https://www.noaa.gov/jetstream/satellites/electromagnetic-waves