
원문 : https://arxiv.org/pdf/2006.11239.pdf
- Diffusion model은 데이터를 만들어내는 deep generative model 중 하나로, data로부터 noise를 조금씩 더해가면서 data를 완전한 noise로 만드는 forward process(diffusion process)와 이와 반대로 noise로부터 조금씩 복원해가면서 data를 만들어내는 reverse process를 활용한다.
- 요즘 생성형 AI모델 중 가장 대중성이 높은 Stable Diffusion 모델이 대표적으로, Diffusion model은 현재 image 쪽에서는 가장 잘 작동하며 사용성이 우수한 생성 모델 중 하나이다.
- 기존 diffusion model은 정의하기 쉽고 훈련하기 효율적이지만 고품질의 샘플을 만들지 못하였는데, 이번에 리뷰할 Denoising Diffusion Probabilistic Models(DDPM)은 기존 Diffusion model에서 생성하는것보다 고품질의 샘플을 만들 수 있을 뿐만 아니라 GAN 등 다른 생성 모델보다 더 우수한 결과를 보였다고 한다.
1. Introduction
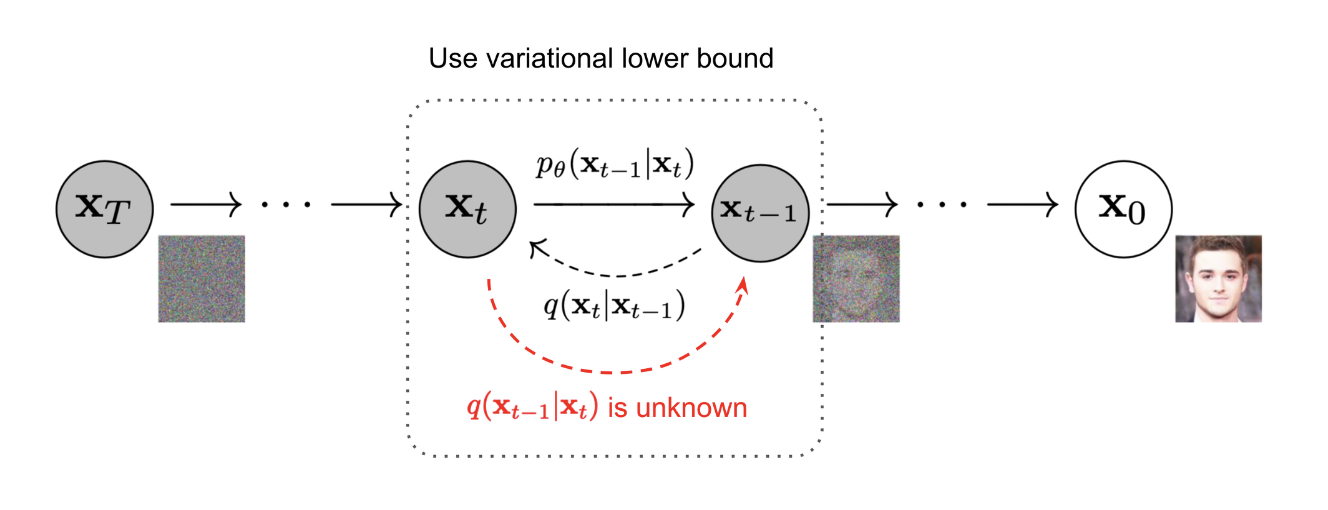
- 위 그림과 같이 DDPM은 주어진 이미지에 작은 gaussian noise를 time에 따라 더해나가는데, 시간이 흐름에 따라 계속해서 이러한 gaussian noise가 이미지에 더해진다면 결국 주어진 이미지는 destroy되어 noise의 형태로 남게 된다.(이때 noise는 일반적인 normal distribution 형태를 가짐) 이후 이러한 normal distribution을 갖는 noise가 주어졌을때 완전히 이미지로 다시 복구가 된다면 image generation하는 것이 Diffusion Model의 일반적인 이미지 생성 원리라고 할 수 있다.
- 본 논문에서 소개하는 DDPM 모델은 유한한 시간 후에 이미지를 생성하는 variational inference을 통해 훈련된 Markov chain을 parameterized한 형태라고 할 수 있다. Markov Chain은 무작위 과정(random process)을 모델링하고 예측하는 데 사용되는 확률적인 모델으로, '상태(state)'라고 불리는 여러 상태들 간의 전이(transition) 확률에 기반하며 특히 다음 상태가 현재 상태에만 의존하는 확률 과정을 나타낸다.
- 즉 DDPM 에서 Forward Process는 Markov Chain 과정을 바탕으로 이전의 샘플링이 현재 샘플링에 영향을 미치는 p(x∣x) 형식을 가지고, 주어진 이미지에 작은 gaussian noise를 점진적으로 계속 더해서 이미지가 완전히 destroy 되게된다.
2. Background
2.1 Forward Process
-
Introduction의 위 그림에서 주어진 원래 이미지를 , 원래 이미지에서 시간의 흐름에 따라 noise를 추가해가는 과정을 라고 하면 에 noise를 적용하여 을 만드는 것을 라고 표현한다.
-
시간 t에 대해 계속해서 noise가 추가된다면 로 표현되고 시간 t가 끝까지 가면 는 완전히 destory된 noise 형태가 된다.
-
이때 원래 이미지 가 주어졌을때 t시간 후 noise가 된 의 분포는 아래 수식으로 표현가능하다.
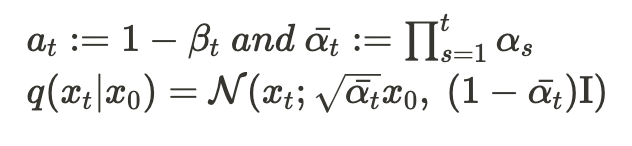
-
이를 DDPM의 Forward process라고 하며, noise -> 이미지를 다시 생성하기 위해서는 Forward Process에서 학습된 의 분포인 를 학습하여야 한다.
2.2 Reverse Process
-
간단히 말해서, Reverse Process는 noise인 에서 원래 이미지인 로 복원(생성)하는 과정이라고 볼 수 있다.
-
즉 Reverse Process는 노이즈로부터 이미지를 생성하는 Generative Model로 동작하기 때문에 앞선 Forward Process에서의 를 모델링하여야 하지만 이를 실제로 알아내는것은 어려운 일이다.
-
따라서 Reverse Process에서는 를 활용하여 를 approximate 하게 되며, 이때 approximate한 는 Gaussian transition을 활용한 Markov chain의 형태를 가지게 된다. 논문에서는 이를 아래 수식과 같이 나타내고 있다.
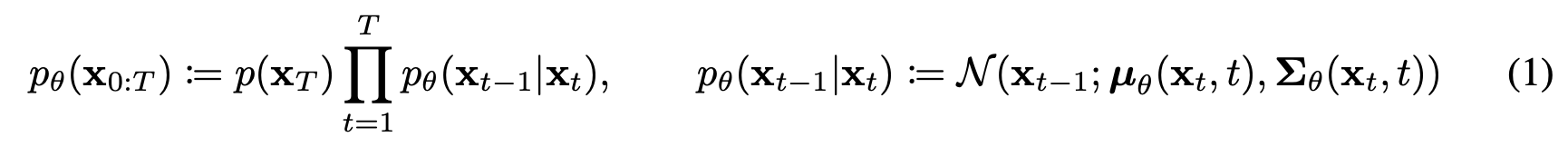
-
위 식에서 와 가 학습 과정에서 최적화되어야 할 파라미터라고 할 수 있다.(DDPM 모델 학습 과정에서 학습 및 최적화하는 부분이 이부분이다.)
2.3 Object Function(목적함수)
-
의 파라미터들을 최적화시키기위해 적용되는 Object Function은 실제 생성하고자 하는 이미지의 분포인 ()를 구하는 것을 목적으로 하며 생성모델인 만큼 ()의 log likelihood를 최대화하여야 하므로 아래와 같은 수식으로 설명할 수 있다.
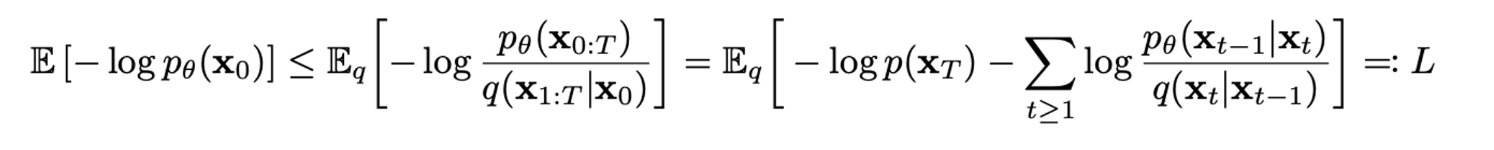
-
논문에서는 reverse process와 forward process를 Markov chain 기반으로 동작한다고 정의하였으므로, Markov property 적용가능하고 Gaussian 분포 간의 KL divergence 형태로 식을 변형하여 아래와 같은 최종 목적함수 식을 도출한다.
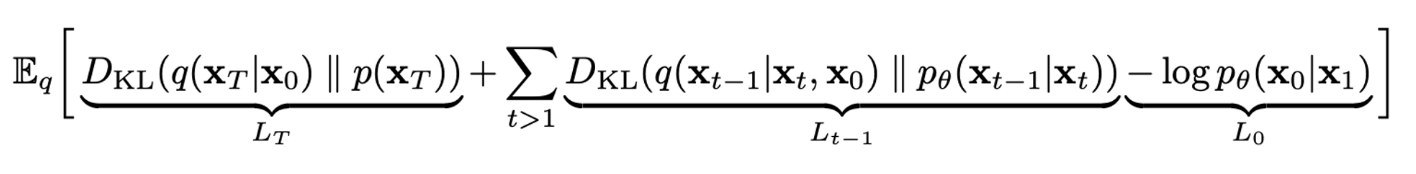
3. Diffusion models and denoising autoencoders
- 위에서 정의된 Forward Process, Reverse Process 및 이를 최적화시키는 Object Function을 바탕으로 샘플링 과정에서 noise를 걷어내며 이미지를 생성할 수 있다.
- 논문을 읽고 이해한 동작방식은 아래와 같다. For문을 따라서 timestep대로 순차적 진행
1) 에서 시간 t가 흐른 후 변화한 , 그리고 이에 대해 예측한 noise가 있음.
2) 수식에서 ,t, noise로부터 를 유도할 수 있다.
3) 유도한 , ,t, noise를 활용하여 수식에서 를 구한다.
4) DDPM은 위 과정을 반복하며 각 timestep에 대한 mean, variance 정보로 그 다음 timestep에 대해 샘플링하는 방식으로 noise를 걷어낸 이미지를 생성한다고 설명할 수 있다.

4. Contribution
- 본 논문에서 소개한 DDPM은 초기 Diffusion 모델이 복잡한 loss function을 사용하여 모델의 복잡도가 높은 단점을 Markov chain과 정규분포를 기반으로 하여 노이즈를 추가하는 Forward process 와 노이즈를 제거하는 Reverse process 두 단계로 이루어진 모델로 구성하고 정규분포의 평균에 해당하는 및 만을 학습시킴으로써 모델이 학습해야 할 파라미터의 범위를 크게 단순화시켜 극복하였음을 알게되었다.
- DDPM 이후 Diffusion 모델이 생성형 모델로 널리 사용되게 되었으며 다양한 분야와 Task에서 Diffusion 모델이 활용되고 있다.
