9252
난이도: 중
문제번호: 9252
생성일: 2021년 4월 1일 오후 10:32
유형: DP, 문자열
출처: https://velog.io/@emplam27/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-LCS-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Longest-Common-Substring%EC%99%80-Longest-Common-Subsequence
문제
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
입력
첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.
출력
첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를, 둘째 줄에 LCS를 출력한다.
LCS가 여러 가지인 경우에는 아무거나 출력하고, LCS의 길이가 0인 경우에는 둘째 줄을 출력하지 않는다.
풀이
'LCS란?'
LCS는 주로 최장 공통 부분수열 (Longest Common Subsequence)를 뜻하나, 상황에 따라서 최장 공통 문자열(Longest Common Substring)을 말하기도 한다.

위 그림에서 최장 공통 부분수열의 경우 연속된 문자가 아니더라도 공통된 부분인 'E'가 추출되는 것에서 두 경우의 차이점을 확인할 수있다.
최장 공통 부분수열 의풀이법 을 알아보기 전에 먼저 최장 공통 문자열의 풀이법을 먼저 살펴보자. (문자열의 풀이법이 수열의 풀이법에 사용되기 때문)
최장 공통 문자열 (Longest Common Substring)
최장 공통 문자열을 찾는 알고리즘의 기본 아이디어는 다음 점화식으로 표현 가능하다.
if(i == 0 || j == 0)
LCS[i][j] = 0;
else if( string_A[i] == string_B[j])
LCS[i][j] = LCS[i-1][j-1] + 1
else
LCS[i][j] = 0 일치하는 문자를 발견했을 경우 그 이전의 문자의 일치가 '연속되었는지' 를 기준으로 판단한다면, DP로 해결 가능한 문제이다. 공통 문자열은 연속되어야 하기 때문에, 현재 두 문자가 같으면, 같은 문자 앞글자 까지의 공통 문자열의 여부를 검사하면 된다.

위의 예시를 사용하면 두 문자열의 비교는 다음과 같이 표시할 수 있다.
(인덱싱 편의상 1칸씩 더 큰 MAP을 0 초기화 한 후 사용한다.)
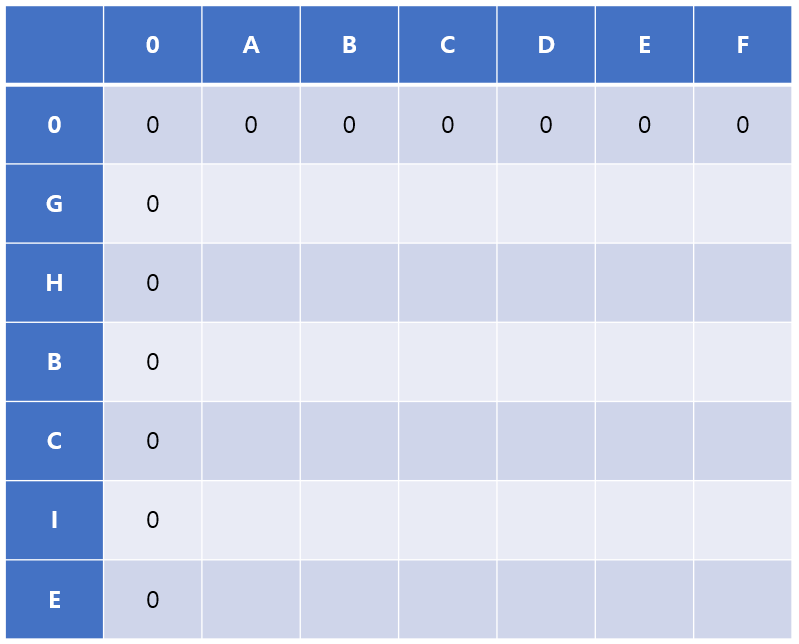
- 먼저 G,H의 값을 '
ABCDEF'의 문자열의 각 문자와 비교한다. 같은 값이 없기 때문에 '0'으로 채워진다.
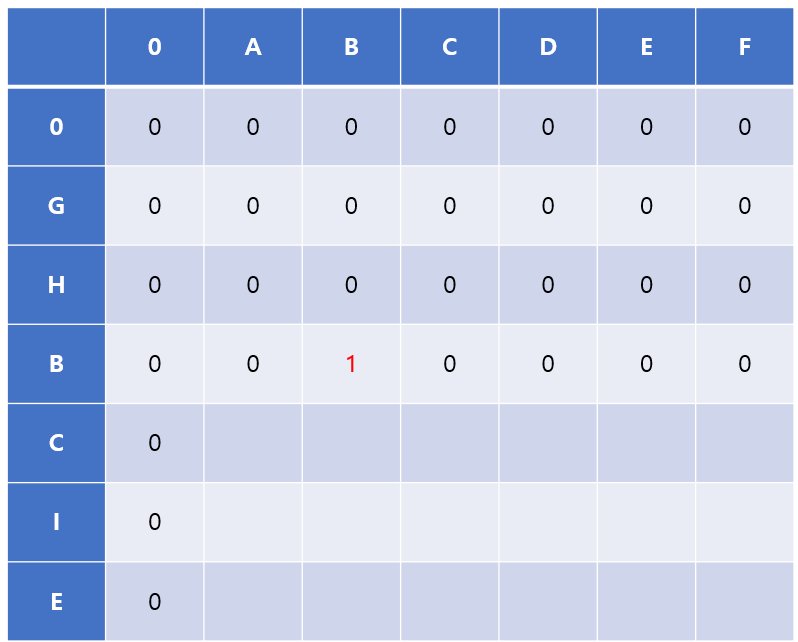
- 다음으로 'B'의 값과 '
ABCDEF'의 문자열의 각 문자를 비교한다. 해당 문자열의 2번째 문자가 'B'임으로LCS[3][2] = LCS[2][1] + 1 = 0 + 1 = 1
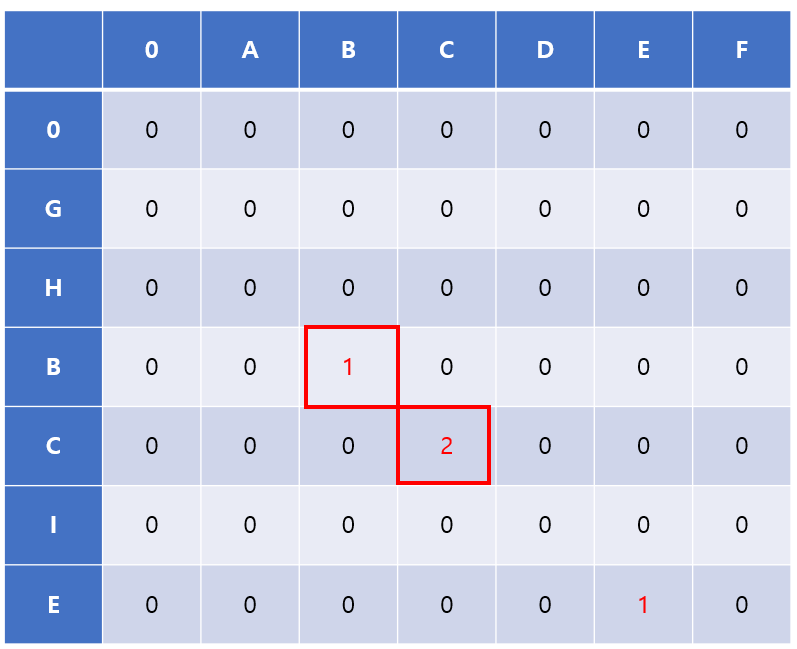
- 다음으로 'C'의 값과 '
ABCDEF'의 문자열의 각 문자를 비교한다. 해당 문자열의 3번째 문자가 'C'임으로LCS[4][3] = LCS[3][2] + 1 = 1 + 1 = 2
위 과정을 남은 모든 문자에 대해 반복하고, 최대값(LCS의 길이) 를 출력한다.
최장 공통 부분수열(Longest Common Subsequence)의 길이
그렇다면 최장 공통 부분 수열을 어떻게 구할 수 있을까
식으로는 다음과 같이 표현될 수 있다.
if(i == 0 || j == 0)
LCS[i][j] = 0;
else if( string_A[i] == string_B[j])
LCS[i][j] = LCS[i-1][j-1] + 1
else
LCS[i][j] = max(LCS[i-1][j], LCS[i][j-1]) 달라진 부분은 최 하단의 else 문으로 각 스트링에서 뽑은 문자가 서로 다를시
LCS[i-1][j]와 LCS[i][j-1]중 큰값을 리턴한다.

부분 수열은 공통 문자열과는 달리 연속된 값이 아니다. 따라서 현재 문자를 비교하는 과정에서, 이전의 쵀대 공통 부분 수열은 계속해서 유지 된다.
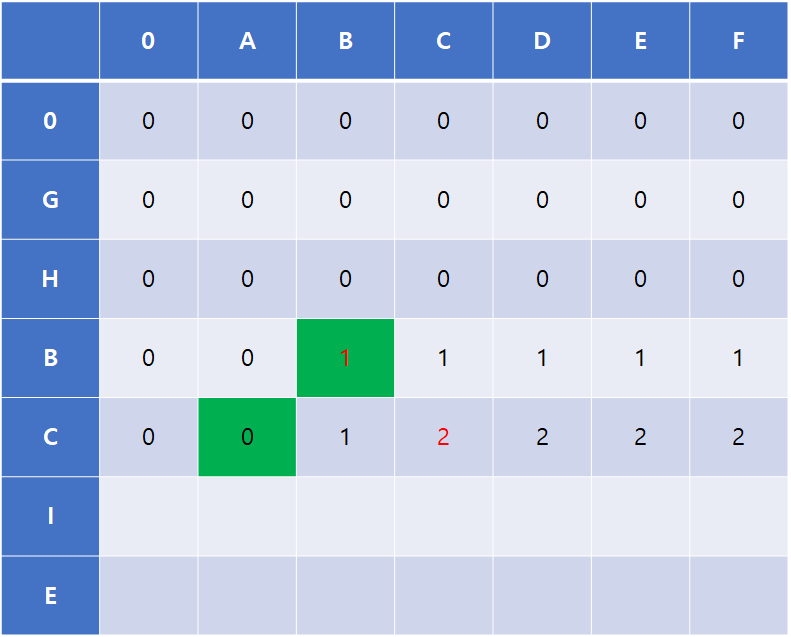
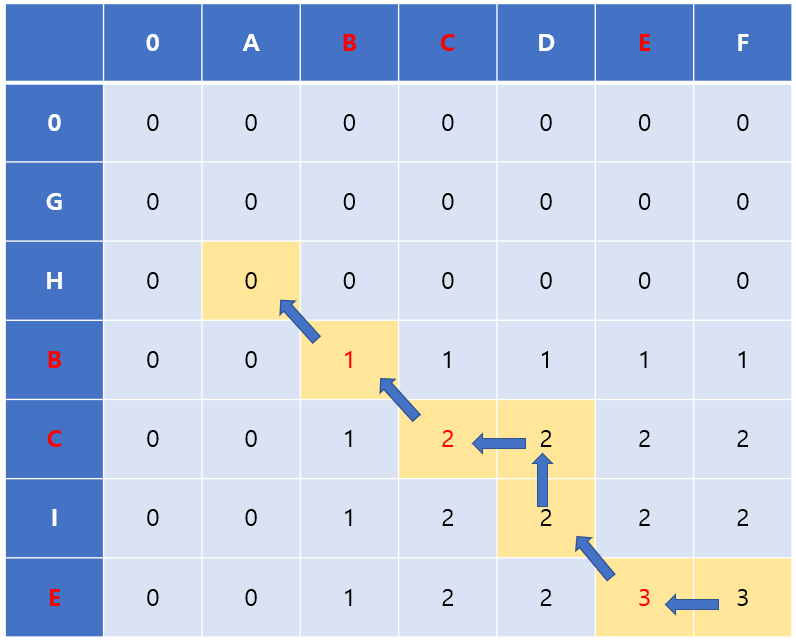
위 그림에서 LCS[4][2]를 구하는 과정 (푸른색 박스)을 보자. LCS[4][2] 의 의미는 글로 풀어 쓰자면 'GHBC'와'AB' 간의 최대 공통 부분 순열이다.
LCS[4][2]의 비교 과정인 'C'와 'B'는 서로 다른 문자이고, 따라서 비교 이전의 최장 공통 부분 순열이 곧 LCS[4][2]의 값으로 유지된다.
비교 이전의 부분이라 함은 두가지, LCS[3][2] , LCS[4][1] 라고 생각 할 수 있다. (초록색 박스)
LCS[3][2] 가 'GHB' 와 'AB'간의 최장 공통 부분수열,
LCS[4][1] 은 'GHBC' 와 'A' 간의 최장 공통 부분 수열을 의미한다.
이 두 값중 더 큰쪽이 최장 공통 부분수열임으로 해당 값이 유지되는 것이다.
이 부분이 이해가 잘 안간다면, LCS[3][2] 이후로 3행의 나머지 값이 1로 유지되는것,
LCS[4][1]이 0인데 LCS[4][2]가 1인것을 다시 확인해 보면 좋다.
역시 모든 문자에 대해 반복하고 최대값을 반환한다.
최장 공통 부분수열 찾기
위의 예시를 다시 사용, 수열을 찾는것은 길이 작성법의 반대 순서와 같다.

코드
```#include <iostream>
#include <cmath>
#include <vector>
#include <algorithm>
#include <string>
using namespace std;
vector<char>ans;
string string_A, string_B;
vector<vector<int>>LCS(1001, vector<int>(1001, 0));
void print(int a, int b, vector<vector<int>>LCS)
{
if (LCS[a][b] == 0) return;
if (LCS[a][b] == LCS[a][b - 1])
b = b - 1;
else if (LCS[a][b] == LCS[a - 1][b])
a = a - 1;
else
{
ans.push_back(string_A[a-1]);
a = a - 1; b = b - 1;
}
print(a, b, LCS);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> string_A >> string_B;
for (int i = 0; i <= string_A.size(); i++)
{
for (int j = 0; j <= string_B.size(); j++)
{
if (i == 0 || j == 0)
LCS[i][j] = 0;
else if (string_A[i-1] == string_B[j-1])
LCS[i][j] = LCS[i - 1][j - 1] + 1;
else
LCS[i][j] = max(LCS[i - 1][j], LCS[i][j - 1]);
}
}
int a = string_A.size();
int b = string_B.size();
cout << LCS[a][b] << endl;
print(a, b, LCS);
for (auto c = ans.rbegin(); c != ans.rend(); c++)
cout << *c;
return 0;
}