Array-1

APS - Algorithm Problem Solving

• 문제를 해결하기 위해 수행해야 하는 절차나 방법
• 목표 : 다양한 알고리즘을 이해하고 문제의 조건에 맞는 좋은 알고리즘을 선택할 수 있게 되는 것
• 순서를 정확하게 이해하고 그에 맞춰 진행하는 것이 필요하다.
• 알고리즘 풀이와 함께 디버깅 경험을 쌓을 수 있다.

• 좋은 알고리즘의 조건 (우선 순위에 따라)
  1. 정확성 : 얼마나 정확하게 작동하는 것인지. 정확하지 않으면 문제 해결이 불가능하다.
  2. 작업량 : 얼마나 적은 연산으로 원하는 결과를 얻어내는가. (실행시간)
  3. 메모리 사용량 : 적은 량의 메모리를 사용하는 것
  4. 단순성 : 다른 사람이 이해하기 쉬운 정도
  5. 최적성 : 더 이상 개선할 여지 없이, 불필요한 알고리즘 제외하여 최적화가 된 것인지.

• 알고리즘을 위한 5단계
  1. 문제를 꼼꼼하게 읽고, 입력 데이터의 범위를 확인
  2. 문제의 조건과 입력 데이터의 범위에 맞는 알고리즘 선택
  3. 코드를 작성하기 전에 풀이를 구상
  4. 구상한 풀이를 코드로 작성한다.
  5. 디버깅하고 검증한다.

• 알고리즘 성능 분석 : 많은 문제에서 성능 분석의 기준으로 알고리즘의 작업량을 비교
• 예시

---

---

알고리즘 표현 방법

1. 의사 코드 (pseudocode)

• 할당 연산자가 = 대신 ← 를 사용
• 다만 엄격하게 따라야 하는 문법이 있는 것이 아니라, 이해를 위해 작성하기만 하면 된다.
• 특정 언어의 구애받지 않고, 알고리즘을 서술할 수 있도록 만들어진다.

2. 순서도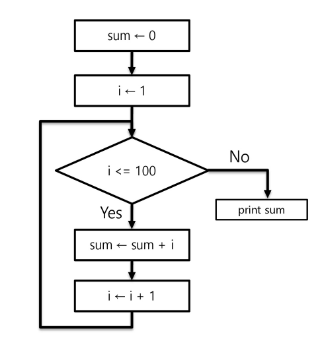

• 프로그램의 절차를 그림으로 이해할 수 있게 나타낸 것
• 조건문은 마름모로 표시

---

---

알고리즘 성능 분석

• 시간 복잡도
  1. 실제 걸리는 시간을 측정 (컴퓨터 성능에 따라 달라질 수도 있다. 절대적인 지표는 X)
  2. 실행되는 명령문의 갯수를 계산 (프로그램이 복잡할수록, 현실적으로 어려움이 있다.
     

• 상수 시간 알고리즘 : 연산량이 커지더라도, 동일한 알고리즘의 시간이 걸리므로 매우 효율적이다.

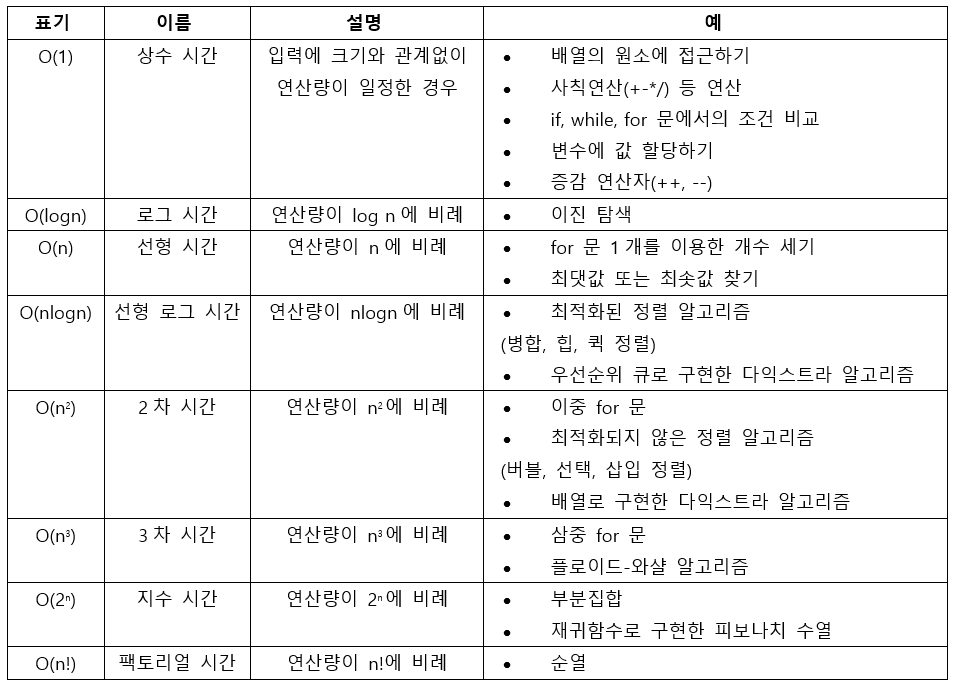
빅-오(O) 표기법

• 시간 복잡도 함수 중에서 가장 큰 영향력을 주는 n에 대한 항만을 표시
• 계수는 생략하여 표시
  

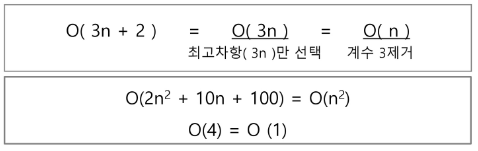
• 성능 비교 시, 최악의 경우만 고려하기 때문에 O(n) 이 O(n^2) 보다 항상 성능이 좋다.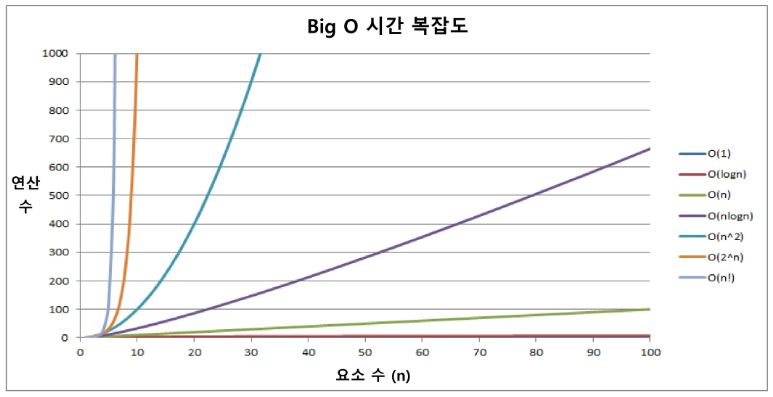

• 연산수 : 실행 시간
• O(1) : 상수 시간 알고리즘 (가장 성능이 좋다.)

• 시간복잡도별 실제 실행 시간 비교

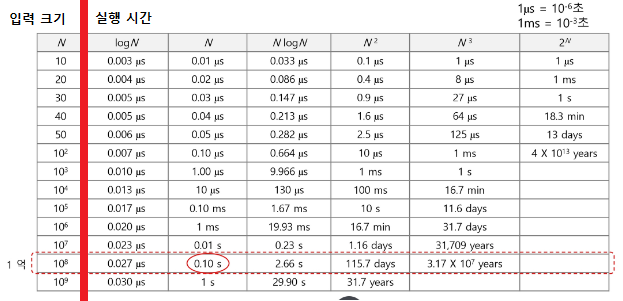
• 주요 시간 복잡도

---

---

자료 구조

• 데이터를 효율적으로 담는 방법 정의
• 데이터의 추가, 조회, 수정, 삭제 연산을 최적화하는 구조
• 프로그램의 목적에 따라 활용할 수 있는, 다양한 자료 구조가 존재한다.

배열

• 프로그램 내에서 여러 개의 데이터를 다뤄야 할 때, 별도의 변수를 선언하는 것보다 하나의 배열로 데이터를 다루는 게 효과적이다.

• 연습 문제

  상자들이 쌓여있는 방이 있다. 방이 오른쪽 90도로 회전하여 상자들이 중력의 영향을 받아 낙하한다고 할 때, 낙차가 가장 큰 상자를 구하여 그 낙차를 리턴하는 프로그램을 작성하시오.
  중력은 회전이 완료된 후 적용된다.
  상자들은 모두 한쪽 벽면에 붙여진 상태로 쌓여 2차원의 형태를 이루며 벽에서 떨어져서 쌓인 상자는 없다
  방의 가로 길이와 세로 길이는 항상 100 이다.
  

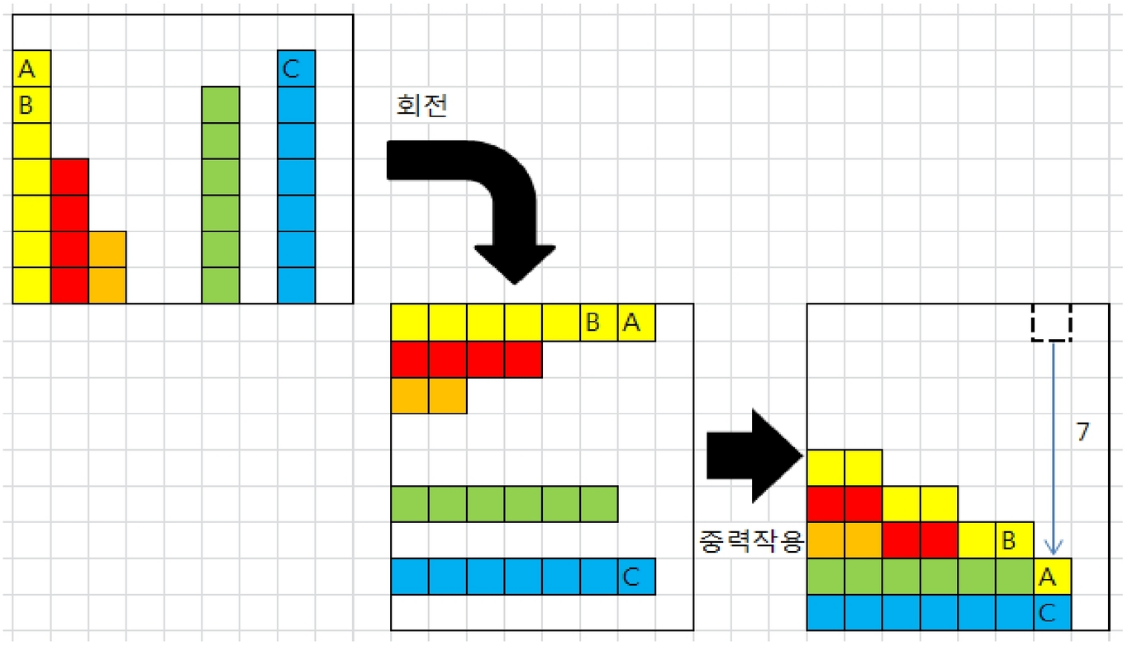
• 기존에 놓여있는 상태로, 인덱스의 빈 칸만 활용하면 회전에 관련된 알고리즘을 작성하지 않아도 괜찮다.

1. 기존에 상자의 높이를 하나의 배열에 넣어주고 시작
2. 가장 높은 상자 더미의 갯수를 센 후에, 낙차의 높이를 구하면 된다.

---

정렬

• 2개 이상의 데이터를 특정 기준에 의해 작은 값부터 큰 값, 혹은 그 반대의 순서대로 재배열 하는 것

• 대표적인 정렬 방식의 종류
  • 버블 정렬
  • 선택 정렬
  • 삽입 정렬
  • 카운팅 정렬
  • 병합 정렬
  • 퀵 정렬
    
    

---

1. 버블 정렬

• 인접한 두 개의 원소를 비교한 후 교환하는 과정을 반복하여 데이터를 정렬하는 방식
• 시간 복잡도 : O(n^2)
  

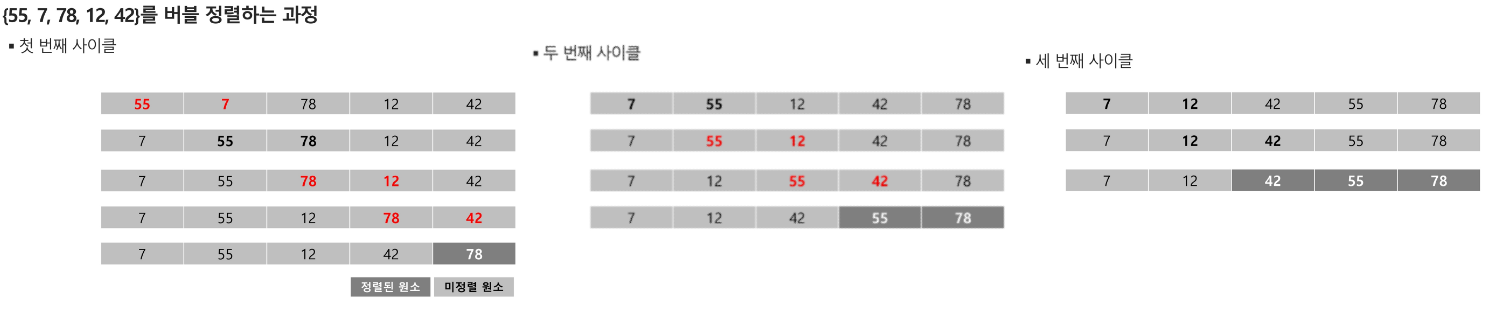
public static void main(String[] args) {
		int[] arr = {55, 7, 78, 12, 42};
		
		// 버블 정렬 
		for (int i = arr.length -1; i > 0; i--) {
			for(int j = 0; j < i; i++) {
				if(arr[j] > arr[j+1]) {
					int temp = arr[j+1];
					arr[j+1] = arr[j];
					arr[j] = temp;
				}
			}
		}
	}