Array-2

zee-chive·2024년 7월 30일
APS
0

APS

목록 보기
2/23

검색

  • 저장되어 있는 자료 중 원하는 항목을 찾는 작업

  • 종류

    • 순차 검색
    • 이진 검색
    • 인덱싱 (데이터 베이스에서 검색하는 방법)



순차검색

  • 일렬로 되어있는 자료를 순서대로 검색하는 방법
  • 배열이나 연결 리스트 등 순차구조로 구현된 자료구조에서 원하는 항목을 찾을 때 유용
  • 단순하여 구현이 쉽지만, 검색 대상의 수가 많은 경우에는 수행 시간이 급격히 증가하여 비효율적.
  • 반복문에 사용 가능

정렬되어 있지 않은 경우

  1. 첫 번째 원소부터 순서대로 검색 대상과 키 값이 같은 원소가 있는지 비교하며 찾는다.
  2. 키 값이 동일한 원소를 찾으면 그 원소의 인덱스를 반환한다.
    • 자료구조의 마지막에 이를 때까지 찾지 못하면 실패
  • 찾고자 하는 원소의 순서에 따라 비교 횟수가 결정.
    (검색에 실패하는 경우, 배열 길이만큼 탐색이 필요하다.)
  • 검색의 성공 여부와 관계 없이, 시간은 O(n)이 된다. 
public class Array2 {
	public static void main(String[] args) {
		int[] arr = {4, 9, 11, 23, 2, 19, 7};
		int key = 2;
		int result = searchForNoSort(arr, key);
		int result2 = searchForNoSort(arr, key);
		System.out.println(result);
		System.out.println(result2);
		
	}
	
	static int searchForNoSort(int[] arr, int key){
		for(int i = 0; i<arr.length; i++) {
			// 값을 찾은 경우
			if(arr[i]==key) return i;
		}
		// 값을 찾지 못한 경우 
		return -1;
	}
	
	static int searchWhileNoSort(int[] arr, int key){
		int cnt = 0;
		
		while(cnt < arr.length) {
			if (arr[cnt] == key) return cnt;
			cnt++;
		}
		
		return -1;
	}
}

정렬되어 있는 경우

  • 자료를 순차적으로 검색하면서, 키 값을 비교하여 원소의 키 값이 검색 대상의 키 값보다 크면 찾는 원소가 없다는 것이므로 더 이상 검색하지 않고 검색을 종료한다.
  • 찾고자하는 원소의 순서에 따라 비교 횟수가 결정된다.
  • 비교 조건이 추가적으로 1개가 더 들어온다.
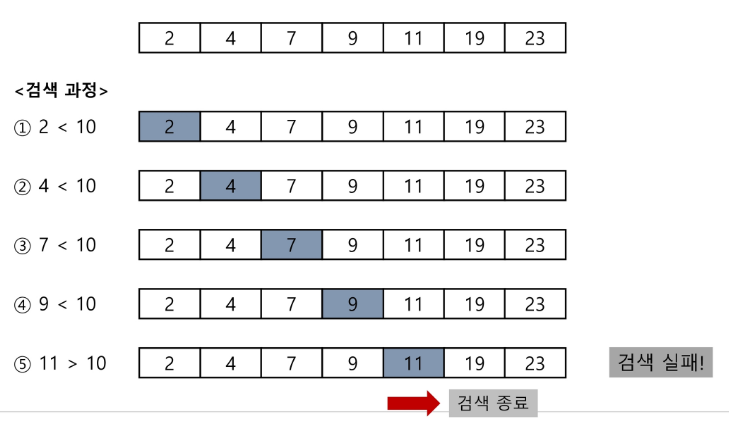
  • 검색의 성공 여부와 관계 없이, 시간은 O(n)이 된다.
    (다만 조금 더 효율적인 결과를 갖고 온다고 할 수 있다. )
public class Array3 {
	public static void main(String[] args) {
		int[] arr = {4, 9, 11, 23, 2, 19, 7};
		int key = 2;
		
		Arrays.sort(arr);
		int result3 = searchForSort(arr, key);
		int result4 = searchWhileSort(arr, key);
		System.out.println(result3);
		System.out.println(result4);
		
	}
	


	static int searchForSort(int[] arr, int key) {	
		// 반복문이 반복을 실행하는 문장이 2개이므로 양이 많아졌다고 할 수 있지만, 
		// 중간에 종료를 확인하게 되는 경우, 반복문의 진행이 적어질 수 있다. 
		for(int i = 0; i<arr.length; i++) {
			if(arr[i] == key) return i;
			else if (arr[i] > key) return -1;
		}
		return -1;
	}
	
	static int searchWhileSort(int[] arr, int key) {
		int cnt = 0;
		
		while (arr[cnt] >= key) {
			if (arr[cnt] == key) return cnt;
		}
		
		return -1;
	}



이진 검색

  • 정렬되어 있는 상태일 때 사용 가능
  • 시간 복잡도 O(log n)
    1. 자료의 중앙에 있는 원소를 고른다.
    2. 중앙 원소의 값과 찾고자하는 목표 값을 비교한다.
    3. 목표 값이 중앙 원소의 값보다 작으면 자료 왼쪽, 크다면 오른쪽에 대해 새로 검색을 수행한다.
    4. 찾고자 하는 값을 찾을 때까지 1~3의 과정을 반복한다.

구현

binarySearch(int[] a, int key) 
	left ← 0;
    right ← length(a) - 1; 
    while ( left 〓 right) {
    	mid = (left+right)/2;
        if(a[mid] == key) return true; // 검색 성공 
        else if (a[mid] > key) right = mid - 1; // 왼쪽으로 이동 
        else left = mid + 1; // 오른쪽으로 이동 
    }
    return false // 검색 실패
  • 코드 실행 
public class 이진검색 {
	public static void main(String[] args) {
		int[] nums = {2, 4, 7, 9, 11, 19, 23};
		
		int result = binarySearch(nums, 10);
		System.out.println(result);
	}
	
	static int binarySearch(int[] arr, int key) {
		// 인덱스 검색이므로 0 과 length-1 을 해줘야 한다. 
		int left = 0;
		int right = arr.length - 1;
		
		// 구간 안에 데이터가 1개 존재한다는 것은 그 값이 맞을 수도 있으므로 
		// left가 커져서 역전되는 값만 아니면 모두 탐색해야 한다. 
		while(left <= right) {
			int mid = (left + right) / 2;
			if (arr[mid] == key) {
				return mid;
			}
			else if (arr[mid] < key) {
				// 중간 값이 검색 값보다 작은 경우 
				// 오른쪽만 확인하면 되는 것이므로, 왼쪽 값을 중앙으로 옮기면 그 후에 오른쪽 확인이 가능하다. 
				left = mid + 1; 
			} else {
				// 중간 값이 검색 값보다 큰 경우 
				right = mid - 1;
			}
		}
		return -1;
	}
}
  • 재귀 함수 이용
    • 자기 자신을 호출하는 함수를 뜻한다. 
binarySearch(int[] a, int left, int right, int key){
	if (left > right) return false; 
    
    mid = (left + right) / 2;
    if(key == a[mid]) return true; 
    else if (key < a[mid]) return binarySearch(a, left, mid -1, key);
    else if (key > a[mid]) return binarySearch(a, mid + 1, right, key);
}



선택 정렬

  • 저장되어 있는 자료로부터 k번째로 작은, 혹은 큰 값의 원소를 찾는 방법
  • 정렬 알고리즘을 이용하여 자료를 정렬하고, 원하는 순서의 원소를 갖고 오면 된다.
  • 1번부터 k 번째까지 작은 원소들을 찾아, 배열의 앞쪽으로 이동시키고, 배열의 k번째를 반환한다.
  • k가 비교적 작을 때 유용하며, O(kn)의 수행 시간을 필요로 한다.
  • 시간 복잡도 O(n^2)
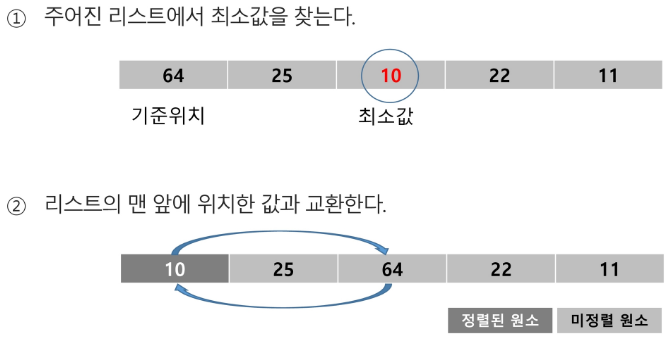
    → 모두 정렬이 될 때까지 해당 방법을 반복하면 된다.
  • 버블 정렬의 경우 사이클마다 자리를 여러 번 변경하여 가장 큰 값을 맨 뒤로 보낸다.
    (인접한 수와 값을 비교하여 매번 변경)
  • 다만 선택 정렬은 자리 변경은 단 한 번만 일어난다. 
public class 선택정렬 {
	public static void main(String[] args) {
		int[] nums = {10, 64, 25, 11, 28, 77, 34};
		
		SelectionSort(nums);
		
		System.out.println(Arrays.toString(nums));
	}
	
	static void SelectionSort(int[] arr) {
		// cycle 횟수는 배열 길이 - 1이 된다. 
		for(int i = 0; i<arr.length; i++) {
			// 최솟값의 인덱스를 저장할 변수
			int minIdx = i;
			for(int j = i+1; j<arr.length; j++) {
				if(arr[minIdx] > arr[j]) minIdx = j;
			}
			
			// 배열 i의 값과, minIdx의 값을 변경해주면 된다. 
			int temp = arr[i];
			arr[i] = arr[minIdx];
			arr[minIdx] = temp;
		}
	}
}



카운팅 정렬

  • 항목들의 순서를 결정하기 위해 집합에 각 항목이 몇 개씩 있는지 세는 작업을 하여, 선형 시간에 정렬하는 효율적인 알고리즘
  • 제한 사항
    • 정수나 정수로 표현할 수 있는 자료에 대해서만 적용 가능
    • 각 항목의 발생 횟수를 기록하기 위해, 정수 항목으로 인덱스 되는 카운트들의 배열을 사용
    • 카운트들을 위한 충분한 공간을 할당하려면, 집합 내 가장 큰 정수를 알아야 한다.
  • 구현 
Counting_sort(int[] A, int[] B, k) 
//A[] - 입력 배열 
//B[] - 정렬된 배열 
//C[] - 카운트 배열
//k - 최대값
//n - 입력 배열 길이 

C = new int[k];

for i from 0 to n 
	C[A[i]] += 1 // 값의 인덱스에 갯수 추가하기

for i from 1 to k 
	C[i] += C[i-1] // 누적합 배열로 만들 것 

for i from n-1 to 0
	B[C[A[i]] -1] = A[i]
    C[A[i]]--
  • 시간 복잡도 : O(n+k) n은 배열의 길이, k는 정수의 최대값 (둘 중 큰 값으로 결정)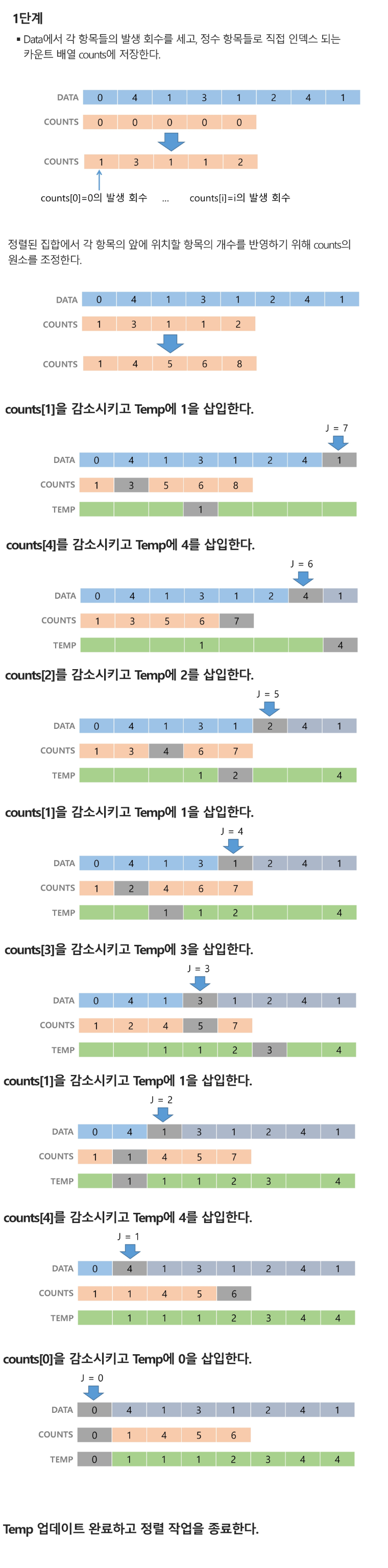
  • 누적합 배열을 신경 쓰면서, 각 원소의 갯수를 확인하면 된다.
  • 해당 원소가 몇 번째 위치까지 나오는 것인지, 확인.
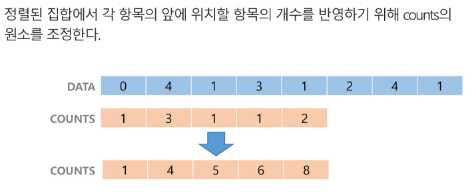
    • 인덱스 값에 따라, <0은 1 번째 위치, 1은 4번째 위치, 2는 5번째 위치...> 이런 방식으로 확인하여 배열 내부에 자리하게 만든다.

  • 카운팅 정렬은 안정정렬(static sort) 라고 부른다.
    • 같은 값을 갖는 배열들은 정렬이 끝난 후에도 정렬 전과 같은 순서를 갖기 때문에.
    • 역순으로 정렬하는 이유는, 그 순서를 유지하기 위해서 진행이 된다.
    • 2차원 배열 정렬의 경우, 하나의 기준으로 진행하게 될 때 나머지 값은 초반의 값 기준으로 남아있게 된다.



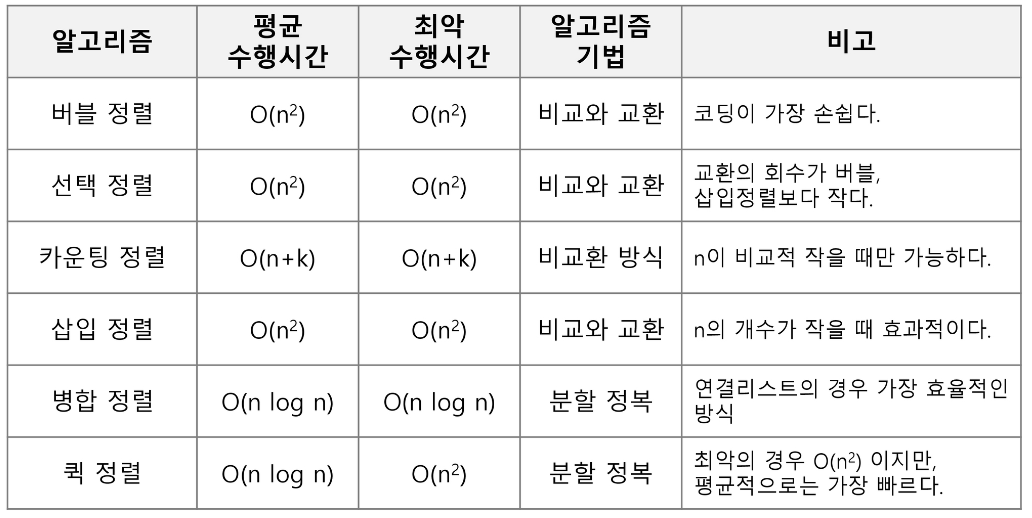
정렬 알고리즘 비교

profile
zee-chive
누가 봐도 읽기 쉬운 글이 최고의 글이다.
이전 포스트

Array-1

다음 포스트

Array-3

0개의 댓글

관련 채용 정보