그래프 탐색

zee-chive·2024년 9월 3일

APS

목록 보기

18/23

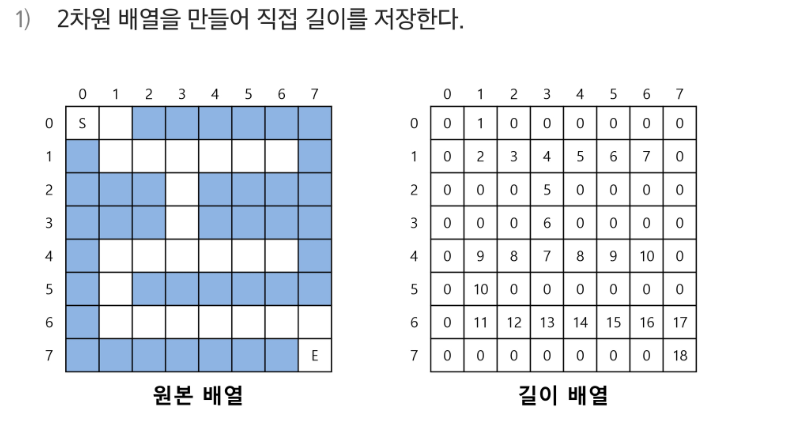
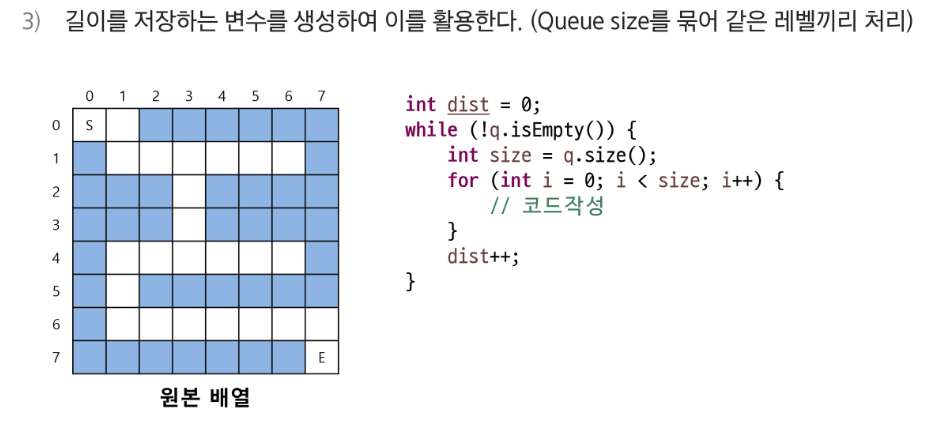
모든 노드를 빠짐 없이 탐색하는 방법은 두 가지가 있다.

깊이 우선 탐색(Depth First Search, DFS)

너비 우선 탐색 (Breadth First Search, BFS)

깊이 우선 탐색 (DFS)

시작 시점에서 출발하여 한 방향으로 탐색
진행할 수 없는 상황이 온다면, 마지막 만난 지점으로 돌아와 다른 방향 다시 탐색
후입선출(LIFO) 구조의 스택(stack) 사용, 재귀 함수는 system stack을 사용하므로 간단한 구현 가능

1. 트리 탐색

루트 노드 → Stack push
Stack 이 empty가 될 때까지 반복 수행
a. 현재 노드를 stack pop 하고
b. 현재 노드의 모든 자식을 stack push

의사 코드

DFS(v){
	stack.push(v)
    while(! stack.isEmpty){
    	curr = stack.pop
        for w in (curr의 모든 자식)
        stack.push(w)
    }
}

2. 재귀 함수를 통한 트리 검색

현재 노드(v) 방문
(v)의 자식 노드 (w)를 차례로 재귀 호출
- 트리 탐색의 경우 자식을 모두 입력한 후 하나씩 호출하지만,
  재귀함수는 모든 자식을 호출 후 형제 노드가 호출이 된다.

다만 그래프의 경우, 단방향이라는 명시가 없다면 양방향으로 A와 B가 반복적으로 탐색할 수도 있다.

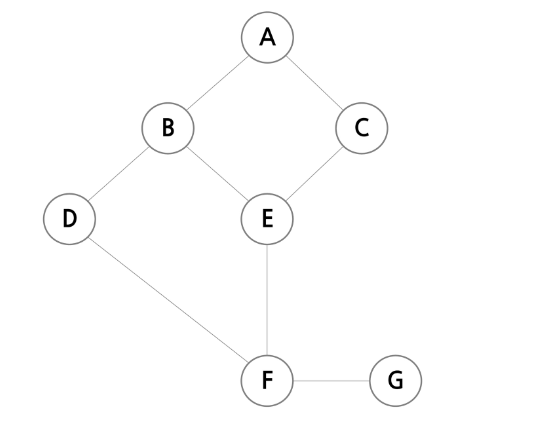
이런 경우, 방문을 처리하기 위한 boolean 함수를 사용해주면 된다.

예시

예시 트리

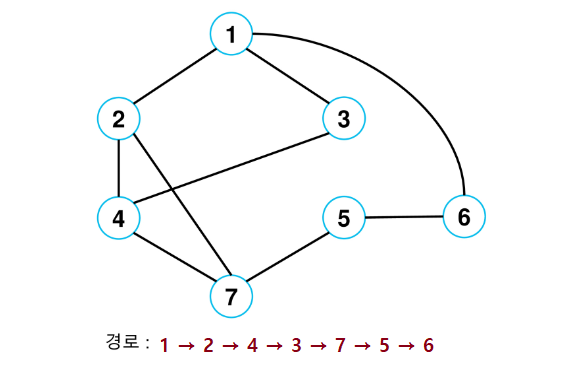
import java.util.Scanner;

public class 그래프탐색01_DFS {
	
	static int V, E; // 정점의 갯수, 간선의 갯수
	static int[][] adj; // 인접행렬
	static boolean[] visited; // 방문 체크 
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		
		V = sc.nextInt();
		E = sc.nextInt();
		
		adj = new int[V+1][V+1]; // 시작 정점의 번호가 1부터 시작하기 때문에 
		visited = new boolean[V+1];
		
		for(int i = 0; i < E; i++) {
			int A = sc.nextInt();
			int B = sc.nextInt();
			
			adj[A][B] = 1;
			adj[B][A] = 1; // 간선 입력 완료
		}	
		
		DFS(1);
	}
	
	// v: 현재 내가 있는 정점 
	static void DFS(int v) {
		
		visited[v] = true;
		System.out.println(v + " -> ");
		
		// 나와 인접하면서 방문하지 않는 정점 방문 
		for(int i = 1; i <= V; i++) {
			//	방문 여부			인접 여부 체크 
			if(!visited[i] && adj[v][i] == 1) { 
				DFS(i);
			}
		}
	}
}

3. 미로 찾기(배열 탐색)

상하좌우 이동하며 고려
다만 경계(미로의 가지 못하는 곳)에 닿으면 안 되고, 벽에 닿으면 안 되며, 방문한 곳을 다시 가면 안 된다.

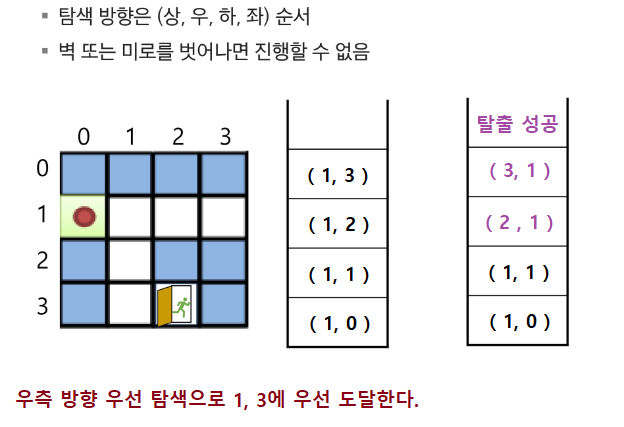
이동 시에 이미 갔던 곳과, 미로의 이동 가능 경로, 그 후에 다른 조건들을 탐색하며 돌아가게 된다.
이동 경로는 nr = r + dr[i] 가 되고, nc = c + dc[i] 라는 방식으로 상하좌우 탐색.
하면서 if(nr < 0 || nr >= N || nc < 0 || nc >= N) 과 같이 경계를 확인하면 된다.

너비 우선 탐색 (BFS)

시작 지점에서 인접한 순으로 탐색을 시작한다
인접한 지점을 모두 방문하였다면, 다음 인접한 지점을 방문한다.
형제 노드를 전부 출력한 후, 그 다음 자식을 찾아 탐색한다.
선입선출(FIFO) 구조의 Queue 자료 구조를 사용한다.
시작 지점과 끝 지점이 주어졌을 때, 최단 길이를 구할 수 있다.

1. 트리 탐색

루트 노드 queue에 삽입
queue가 공백이 될 때까지 반복 수행
a. queue 에서 원소 curr 꺼내기
b. 해당 원소 방문
c. curr의 자식 노드 queue에 삽입

수도코드

BFS(v){
	Queue 생성
    Queue.add(v)
    
    while (!Queue.isEmpty()){
    	curr ← Queue.deq()
        curr 방문
        for w in (curr의 모든 자식 노드){
        	Queue.add(w)
        }
    }
}

2. 그래프 탐색 실습

큐를 생성
시작 노드 V를 큐에 삽입하고, 방문한 것으로 표시한다.
큐가 비어있지 않는 경우, 큐의 첫 번째 원소 T를 반환
a. T와 연결된 모든 선에 대해 방문되지 않는 곳이면 큐에서 출력 후, 방문한 곳으로 처리

만약 2 번에서 방문 표시를 하는 것이 아니라, 원소를 반환할 때 방문 처리를 하게 되면 중복이 발생하여 비효율적이다.

자바 구현

public class 그래프탐색01_DFS {
	static int V, E; // 정점의 갯수, 간선의 갯수
	static List<Integer>[] adj; // 인접 리스트
	static boolean[] visited; // 방문 체크 
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		
		V = sc.nextInt();
		E = sc.nextInt();
		
//		adj = new ArrayList[V+1]; 배열만 생성한 것이고, 안에 리스트 생성 필요 
		
		for(int i = 1; i < V; i++) { // 1번 정점부터 시작하기 때문에 
			adj[i] = new ArrayList<>(); 
		}
		
		visited = new boolean[V+1];
		
		for(int i = 0; i < E; i++) {
			int A = sc.nextInt();
			int B = sc.nextInt();
			
			adj[A].add(B);
			adj[B].add(A);

		}	
		
	}
	
	// 시작 정점 v 삽입
	static void BFS(int v) {
		Queue<Integer> q = new LinkedList<>();
		
		// 시작 정점을 넣고, 방문을 체크한다. 
		q.add(v);
		visited[v] = true;
		
		// 큐가 공백 상태가 아닐 때까지 돌겠다는 의미 
		while(!q.isEmpty()) {
			int curr = q.poll(); // 정점을 한 개 꺼낸다.
			System.out.println(curr);
			
			// curr의 인접하면서 방문하지 않은 정점을 방문 
			for(int w : adj[curr]) {
				if (!visited[w]) {
					q.add(w);
					visited[w] = true;
				}
			}
			
			/* for(int i = 0; i < adj[curr].size(); i++){
				int w = adj[curr].get(i)
			}
			와 동일하다. 
			*/
		}
	}
	

}

3. 미로 찾기(배열 탐색)