그래프 비용

상호 배타 집합

• 중복 포함된 원소가 없는 집합 → 교집합이 없다.
• 각 집합은 대표자를 통해 구분

• 표현 방법
  • 연결 리스트
  • 트리

• 상호 배타 집합 연산
  • Make-Set(X) : X라고 하는 원소를 대표자로 하는 집합 생성
  • Find-Set(x) : x가 속한 대표 집단 찾기
  • Union(x,y) : x와 y의 집합을 하나로 만드는 것. 대표가 x가 된다.

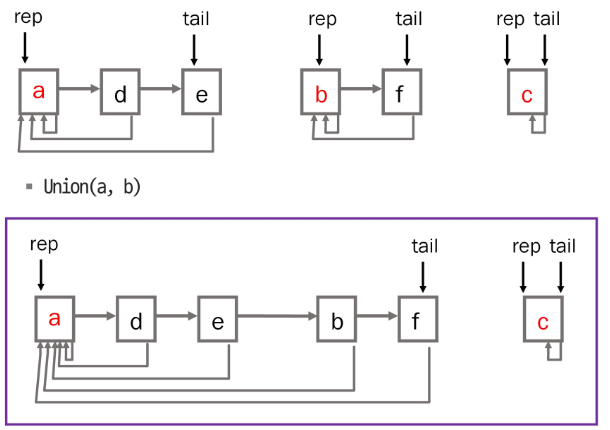
상호 배타 집합 표현 - 연결 리스트

• 같은 집합의 원소들은 하나의 연결 리스트로 관리
• 연결 리스트의 맨 앞 원소를 집합의 대표자로 결정
• 각 원소는 집합의 대표 원소를 가리키는 링크를 갖는다.

상호 배타 집합 표현 - 트리(배열로 만들기)

• 하나의 집합을 하나의 트리로 표현한다.
• 자식 노드가 부모 노드를 가리키며, 루트 노드가 대표자가 된다.

• union의 경우, 대표자를 찾아서 연결하게 된다.

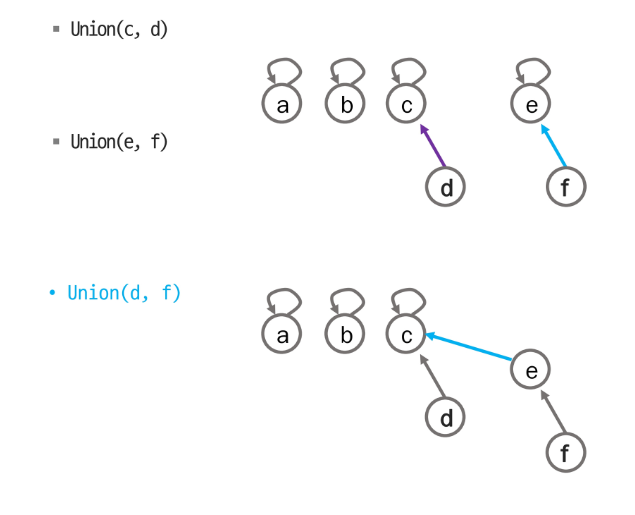
• 이 경우, f가 대표는 e가 되고, 그 e의 대표자인 c가 최종 대표가 된다.

union(x,y)
	p[find-set(y)] ← find-set(x)

연산의 효율을 높이는 방법

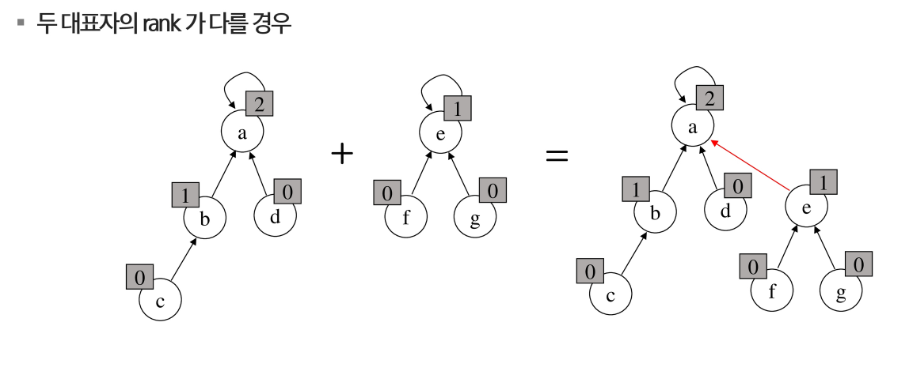
1. Rank를 이용한 Union
   • 각 노드는 자신을 루트로 하는 subtree의 높이를 rank라는 이름으로 저장
   • 두 집합을 union 할 때, rank가 낮은 집합을 높은 집합에 붙인다.
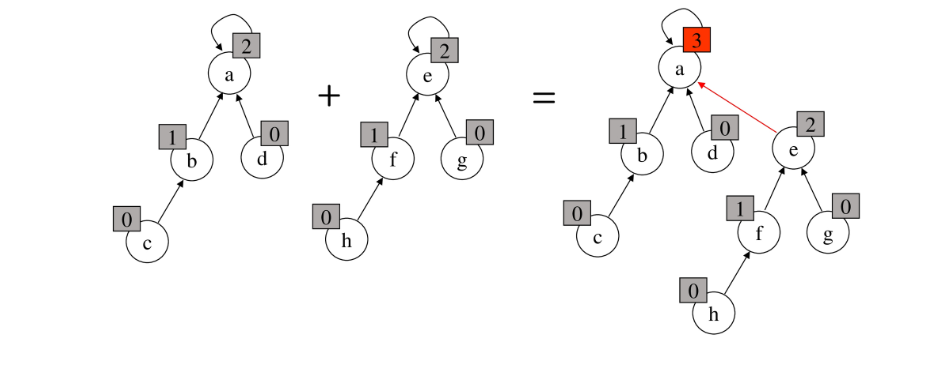
   • 만약 두 rank가 동일한 경우, 아무 곳에다 붙이고, 루트가 되는 rank를 하나 높여준다.

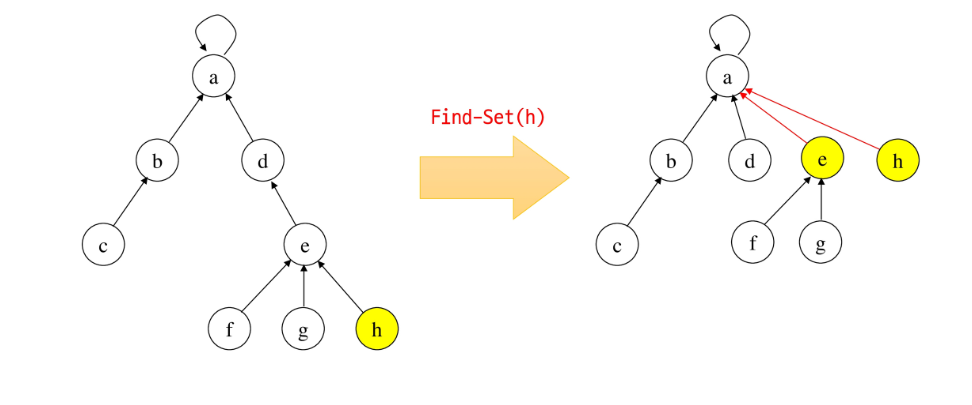
2. Path Compression
   • 직접 루트를 가르킬 수 있도록 변경
   • Find-Set을 행하는 과정에서 만나는 모든 노드들이 직접 대표를 가리키도록 수정한다.

💡 Make-Set( ) 연산

p[x] : 노드 x의 부모 저장 
rank[x] : 루트 노드가 x인 트리의 랭크 값 저장 
make-set(x) 
	p[x] = x
    rank[x] = 0

💡 Find-Set( ) 연산

find-set(x)
	if (x != p[x]) p[x] = find-set(p[x]) 
    // x가 루트가 아닌 경우, 노드의 부모를 찾아 가는 재귀 활용 
    return p[x]

💡 Union-Set( ) 연산

union(x,y)
	if ( rank[x] > rank[y] ) p[y] = x // rank는 트리의 높이
    else 
    	p[x] = y
        if (rank[x] == rank[y]) rank[y]++