컴퓨터 수 표현

진법

• 수를 표현하는 기수법의 하나

10진법

• 진수가 10인 진법
• 0 - 9까지의 10개 숫자를 사용

• 2진법의 경우, 컴퓨터 내부에서 데이터를 처리하는 데 주로 사용한다.
• 8진법은 과거에 컴퓨터 시스템에서 메모리 주소를 간략하게 표현하기 위해 사용했지만, 이제는 16진법을 사용한다.

• 모두 2의 배수가 된다.
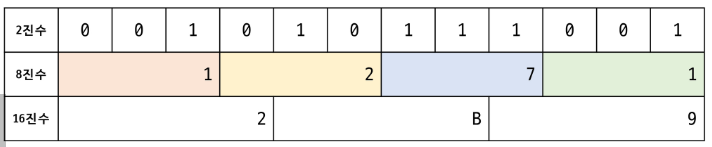
• 프로그래머 계산기에서도 확인이 가능하다

• 반대로 하는 것은, 각각의 진수를 곱해 10진수로 변경할 수 있다.

부호 비트

• 음의 정수 표현 방법
  • 최상위 비트를 부호 비트로 사용 ( 양수 → 0 / 음수 → 1 )
  • 나머지 비트는 숫자의 크기를 표현한다.
  • 양수와 음수의 표현이 직관적이고, +0, -0 이 모두 존재하여, 계산시 비효율적이기는 하다.
  • 두 수의 덧셈과 뺄셈이 복잡해진다.

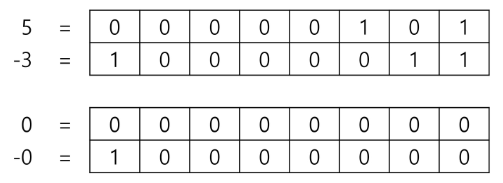
• 음의 정수 표현 방법 (1의 보수)
  • 비트의 값을 반전시켜, 주어진 숫자를 다른 형태로 표현하는 것
  • 양수와 음수의 표현이 서로 반대이다. (비트 반전을 통해 표현이 가능하다)
  • 덧셈, 뺄셈 연산 시 캐리 비트(올림 혹은 내림)를 고려해야 한다.

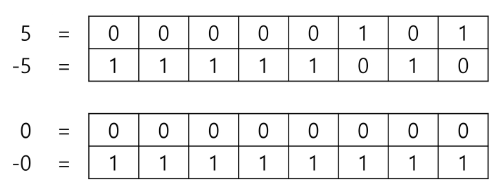
• 음의 정수 표현 방법 (2의 보수)
  • 컴퓨터 시스템에서 음수를 표현하는 가장 일반적인 방법
  • 단 하나의 0만 존재하게 된다. 두 값을 더했을 때 모두 0이 되어버린다.
  • 절대값으로 이진수 진행 후, 마지막에 1을 더해주면 완료가 된다.
  • 덧셈과 뺄셈을 동일한 방식으로 처리가 가능하다.
  • 비트를 반전 시킨 후에, 가장 뒤에 +1을 해주면 된다.

• 실수의 표현
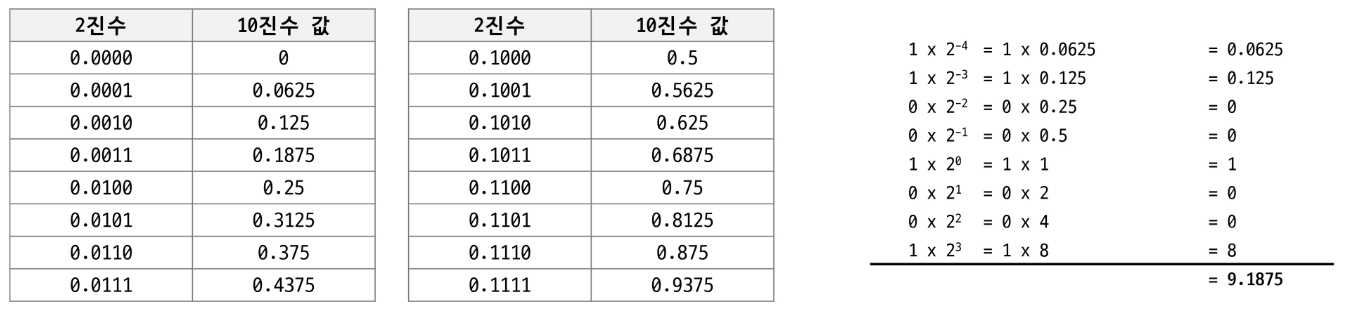
  • 2진수 소수점 이하 4자리 값을 10진수로 표현한 방법

실수의 표현 1 - 고정 소수점

• 소수점 위치가 고정된 상태로 숫자를 표현
• 정수부와 소수부의 비트 수가 고정되어 있다.
• 구현이 간단하고 계산이 빠르지만, 나타낼 수 있는 숫자 범위가 제한적이다. (범위가 작다)
• 부호를 위한 비트 + 정수를 위한 비트 + 소수를 위한 비트

실수의 표현 2 - 부동 소수점

• 가수와 지수로 분리하여 숫자를 표현한다.
• 소수점의 위치를 왼쪽의 가장 유효한 숫자 다음으로 고정시키고, 밑 수의 지수 승으로 표현한다.

---

비트 연산자

• 주어진 숫자를 2진수로 표현한 후, 각 비트를 개별적으로 연산하는 방식
• 종류
  • AND 연산자 : &
  • OR 연산자 : |
  • XOR 연산자 : ^
  • NOT 연산자 : ~
  • SHIFT 연산자 : << , >> , >>>

& (AND 연산자)

• 두 숫자 간의 AND 연산을 통해 특정 비트가 모두 1인 것인지 확인
• 5 & 3 = 1

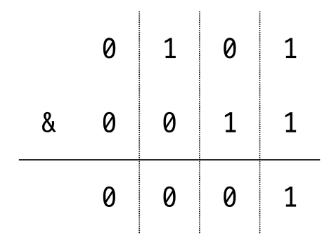
| (OR 연산자)

• 두 숫자 간의 OR 연산을 통해, 특정 비트가 1인지 확인 ( 둘 중 한 개 이상이 1이면 1)
• 5 | 3 = 1

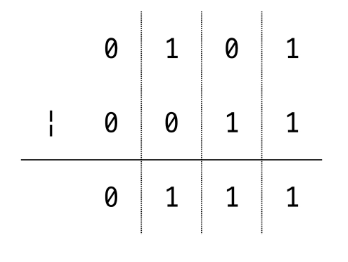
^ (XOR 연산자)

• 두 숫자 간의 XOR 연산을 통해, 특정 비트가 다를 때만, 1이 된다.
• 암호화와 복호화에 사용할 수도 있다.
• 5 ^ 3 = 6

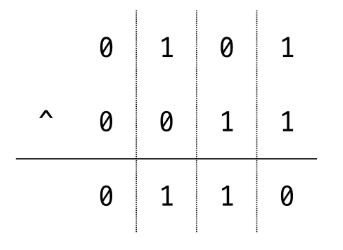
~ (NOT 연산자)

• 숫자의 모든 비트를 반전 시키는 예시, 1의 보수를 시키는 것이다.
• ~5 = -6

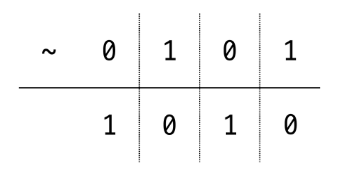
SHIFT 연산자

• << : 비트를 왼쪽으로 이동시키고, 오른쪽에 0을 채워 넣는 연산
• >>
  • 비트를 오른쪽으로 한 칸씩 이동시키고, 왼쪽에 부호 비트를 채워 넣는 연산
  • 기존에 0이었으면, 0을 채워버리고, 1이었다면 1을 채워 넣는다.
• >>> : 비트를 오른쪽으로 이동시키고, 왼쪽에 0을 채워 넣는 연산