힙
완전 이진 트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해서 만든 구조
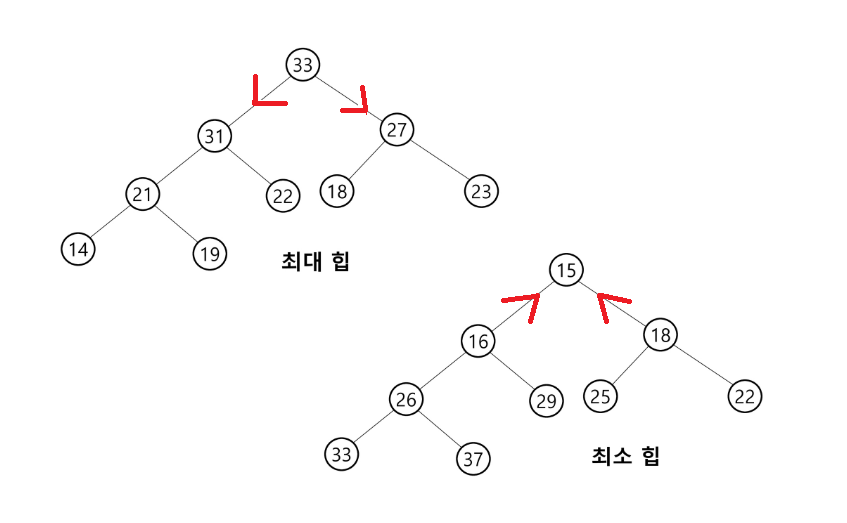
- 최대 힙
- 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리
- 부모 노드의 키 값 >= 자식 노드의 키 값
- 루트 노드 : 키 값이 가장 큰 노드
- 최소 힙
- 키 값이 가장 작은 노드를 찾기 위한 완전 이진 트리
- 부모 노드의 키 값 <= 자식 노드의 키 값
- 루트 노드 : 키 값이 가장 작은 노드
특징
1. 완전 이진트리
2. 부모 자식의 대소 관계가 항상 일정해야 한다.
< 힙이 아닌 이진 트리 >
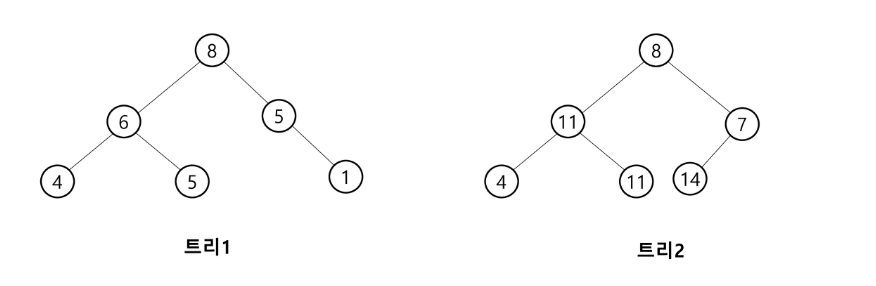
트리 1 : 완전 이진 트리가 아니기 때문에 힙이 아니다.
트리 2 : 완전 이진 트리가 아니며, 대소 관계가 일정하지 않다.
삽입
최대 힙에 루트보다 큰 값을 대입하는 경우
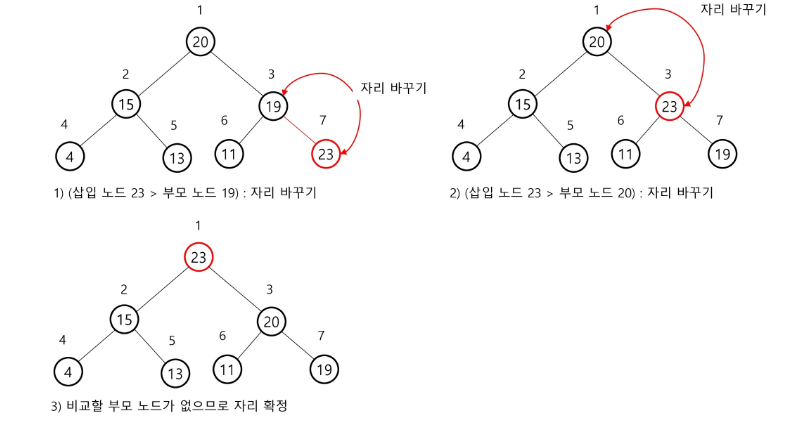
삽입 연산이 일어나는 경우, 부모와 비교만 하면 된다.
완전 이진 트리가 되어야 하므로, 가장 왼쪽부터 비어있는 공간에 삽입하게 된다.
부모와 자식이 같은 값인 경우, 변경하지 않아도 된다.
루트에 가장 대소관계가 가장 크거나 작은 값이 오는 것이 중요하다.
그 내부에 있는 값들의 변화는 크게 중요하지 않다.
삭제
- 힙에서는 루트 노드의 원소만 삭제할 수 있다.
- 루트 노드의 원소를 삭제하여 반환한다.
- 힙의 종류에 따라 최대값 또는 최소 값을 구할 수 있다.
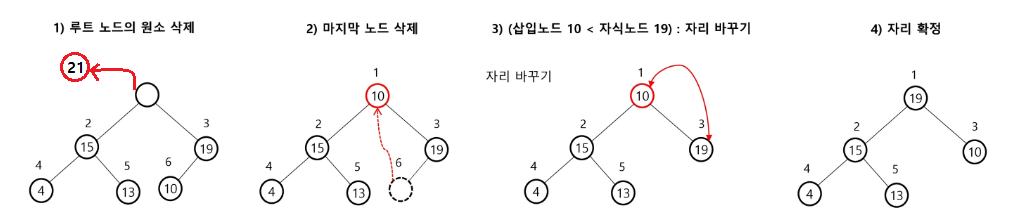
- 가장 큰 값 21을 삭제하고 난 후, 정렬하는 그림이라 생각하면 된다.
- 2번과 같이 루트에 들어간 경우, 왼쪽 자식과 오른쪽 자식 중 힙의 유지를 위해 더 큰 자식(혹은 더 작은 자식) 과 자리를 바꿔주면 된다.
완전 이진 트리를 유지하는 이유
- 배열 구현이 쉽다.
- 부모와 자식 관계 ( root * 2)이 일정하게 사용할 수 있어 효율적이다.
- 메모리의 낭비를 최소화하면서 이용하기 쉽다.
Heap 구현
public class tree_최소힙 {
static int[] heap = new int[100];
static int heapSize = 0;
public static void main(String[] args) {
heapPush(20);
heapPush(19);
heapPush(18);
heapPush(-5);
heapPush(40);
heapPush(-18);
// pop을 하게 되면 heapSize가 줄어들어서,
// 전부 나오는 것이 아니라, 절반만 나오게 된다.
// 따라서 사이즈를 별도로 지정한 후, 고정 값으로 출력을 해야 한다.
int size = heapSize;
for(int i = 0; i < size; i++) {
int popItem = heapPop();
System.out.println(popItem);
}
// 혹은 while (heapSize != 0) 이라는 조건으로 진행해도 된다.
}
// 삽입과 삭제를 함께 하는 경우, swap에 대한 메소드 지정해도 된다.
static void swap (int i, int j) {
int tmp = heap[i];
heap[i] = heap[j];
heap[j] = tmp;
}
// 삽입 연산
static void heapPush(int data) {
//완전 이진 트리 마지막에 데이터 추가
// 0번 인덱스는 사용하지 않기 때문에 + 1 을 해준다.
heap[++heapSize] = data;
int parent = heapSize / 2;
int child = heapSize;
// 계속 반복하여 루트까지 올라가야 하므로 while 사용
// 자식 인덱스가 1인 경우, 루트에 도달한 것이므로, while문을 종료해야 한다.
while (child != 1 &&heap[parent] > heap[child] ) {
int tmp = heap[parent];
heap[parent] = heap[child];
heap[child] = tmp;
// swap(parent, child);
// 스왑을 하게 된 경우, 인덱스 갱신이 필요.
child = parent;
parent = child / 2;
}
}
// 삭제 연산
static int heapPop(){
// 1. 루트에 있는 데이터 저장
int popItem = heap[1];
// 2. 마지막 노드를 루트로 옮긴다.
// 옮긴 후에 heapSize를 하나 줄여야 하므로, 증감 연산자 사용
heap[1] = heap[heapSize--];
// 3. heap이 조건을 유지하기 위해, 자식과 부모를 비교하여 swap 진행하면 된다.
int parent = 1;
int child = parent * 2;
// 자식이 만약 왼쪽과 오른쪽 모두 있다면,
// 둘 중 한 명을 비교하여 더 작은 쪽으로 swap을 진행해야 한다.
if (child + 1 <= heapSize && heap[child] > heap[child+1]) {
child = parent * 2 + 1;
}
while (child <= heapSize && heap[child] < heap[parent]) {
swap(parent, child);
// 부모보다 작은 경우, 인덱스 갱신
parent = child;
child = parent * 2;
if (child + 1 <= heapSize && heap[child] > heap[child+1]) {
child = parent * 2 + 1;
}
}
return popItem;
}
}활용 1 - 우선순위 큐
- 우선 순위 큐를 구현하는 가장 효율적인 방법이 힙을 사용하는 것이다.
- 노드 하나의 추가, 삭제의 시간 복잡도가
O(logN)이고, 최대, 최소 값은O(1)에 구할 수 있다. - swap 은 최대 레벨의 수만큼 일어날 수도 있다.
- 완전 정렬보다 관리 비용이 적다.
- 노드 하나의 추가, 삭제의 시간 복잡도가
- 구현을 쉽게 할 수 있다.
- 부모나 자식 노드를
O(1)연산으로 쉽게 찾을 수 있다. - n 위치에 있는 노드의 자식은
2*n과2*n+1에 위치한다. - 완전 이진 트리의 특성에 의해 추가, 삭제의 위치는 자료의 시작과 끝 인덱스로 쉽게 판단할 수 있다.
- 부모나 자식 노드를
- java.util.PriorityQueue 라이브러리 사용하며 쉽게 쓸 수 있다.
- 기본적으로 최소 heap을 기준으로 작성이 된다.
- 최대 heap으로 진행하는 방법 :
- 입력하는 경우에 음수 기호
-를 붙여서 진행, 출력에 다시-를 붙여서 출력한다. - reverseOrder를 진행하면 된다. (하단에 진행)
- 입력하는 경우에 음수 기호
import java.util.Collections;
import java.util.PriorityQueue;
public class Tree2_우선순위 {
public static void main(String[] args) {
PriorityQueue<Integer> pq = new PriorityQueue<>();
pq.add(10);
pq.add(20);
pq.add(30);
pq.add(-10);
pq.add(40);
while(!pq.isEmpty()) {
int data = pq.poll();
System.out.println(data); //-10 10 20 30 40
}
PriorityQueue<Integer> pq2 = new PriorityQueue<>(Collections.reverseOrder());
pq2.add(10);
pq2.add(20);
pq2.add(30);
pq2.add(-10);
pq2.add(40);
while(!pq2.isEmpty()) {
int data = pq2.poll();
System.out.println(data); //40 30 20 10 -10
}
}
}- 여러 데이터가 들어가는 class 를 정렬하고 싶은 경우 : Comparable 사용한다.
import java.util.Collections;
import java.util.PriorityQueue;
class Person implements Comparable<Person>{
String name;
int age;
Person(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public int compareTo(Person o) {
// 입력되는 o 값은 상대방을 의미한다 .
// 리턴값 : -1(위치를 유지한다), 0(동일하다), 1(위치를 바꾼다)
if (this.age == o.age) return 0;
else if (this.age > o.age) return 1;
else return -1;
}
@Override
public String toString() {
return this.name + " : " + this.age;
}
}
public class Tree2_우선순위 {
public static void main(String[] args) {
PriorityQueue<Person> personPQ = new PriorityQueue<>();
personPQ.add(new Person("luna", 3));
personPQ.add(new Person("daisy", 1));
personPQ.add(new Person("max", 8));
while(!personPQ.isEmpty()) {
Person P= personPQ.poll();
System.out.println(P); // daisy : 1 luna : 3 max : 8
}
}
}
활용 2 - 힙 정렬
- 힙 정렬은 힙 자료구조를 이용하여 이진트리와 유사한 방법으로 수행된다.
- 배열에 저장된 자료를 정렬하기에 유용
- 정렬 2 단계
- 하나의 값을 힙에 삽입한다.(반복)
- 힙에서 순차적으로 (오름차순) 값을 하나씩 제거한다.
최대 값 몇 개를 알아내기에는 용이함.
- 힙 정렬의 시간 복잡도
- 삭제와 삽입 연산 :
O(logN) - 전체 정렬 :
O(N logN)
- 삭제와 삽입 연산 :